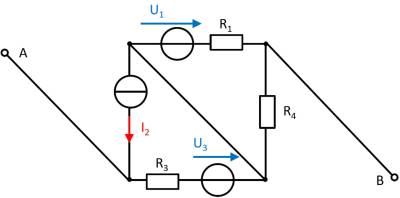
Exercise 4.5.3 -Variation: open circuit voltage via superposition (exam task, approx. 12 % of a 60-minute exam, WS2020)
A circuit is given with the following parameters
$R_1=5 ~\Omega$
$U_1=2 ~{\rm V}$
$I_2=1 ~{\rm A}$
$R_3=20 ~\Omega$
$U_3=8 ~{\rm V}$
$R_4=10 ~\Omega$
Determine the open circuit voltage between A and B using the principle of superposition.
\begin{align*} U_{\rm AB,1} = \frac{R_4}{R_1+R_4} U_1 = \frac{10~\Omega}{5~\Omega+10~\Omega} \cdot 2~{\rm V} = 1.33~{\rm V} \end{align*} Case 2: For this case is $U_1 = 0~{\rm V}$ and $U_3 = 0~{\rm V}$. The voltage is at $R_3$.
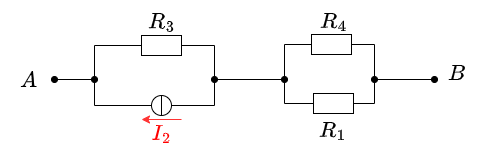
\begin{align*} U_{\rm AB,2} = R_3 I_2 = 20~\Omega \cdot 1~{\rm A} = 20~{\rm V} \end{align*} Case 3: For this case is $U_1 = 0~{\rm V}$ and $I_2 = 0~{\rm A}$. The voltage comes from the source $U_3$.
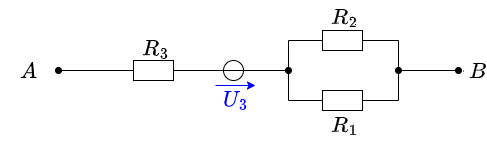
\begin{align*} U_{\rm AB,3} = 8~{\rm V} \end{align*} Superposition means adding the voltages of all three cases. \begin{align*} U_{\rm AB} = U_{\rm AB,1} + U_{\rm AB,2} + U_{\rm AB,3} = 1.33~{\rm V} + 20~{\rm V} + 8~{\rm V} \end{align*}