Aufgabe 5.2.1 mehrere Kräfte auf eine Ladung I (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
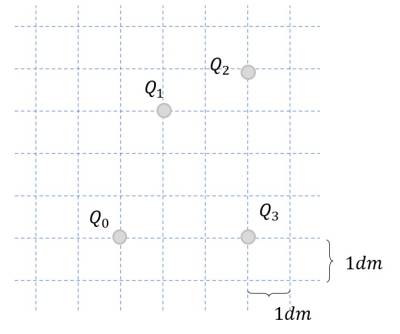
Gegeben ist die die Anordnung elektrischer Ladungen im Bild rechts.
Es ergeben sich folgende Kraftwirkungen:
$F_{01}=-5 N$
$F_{02}=-6 N$
$F_{03}=+3 N$
Ermitteln Sie rechnerisch die den Betrag der resultierenden Kraft.
- Wie müssen die Kräfte vorbereitet werden, dass sie tatsächlich addiert werden können?
Die vorhandenen Kräfte müssen in Koordinaten zerlegt werden. Hier empfehlen sich die orthogonalen Koordinaten ($x$ und $y$).
Das Koordinatensystem sei so ausgelegt, dass der Ursprung in $Q_0$ liegt mit der x-Achse in Richtung Q_3 und die y-Achse entsprechend rechtwinklig dazu.
Zur Koordinatenzerlegung sind die Winkel $alpha_{0n}$ der Kräfte zur x-Achse notwendig.
Diese ergeben sich im gewählten Koordinatensystem aus den Koordinaten der Ladungen: $\alpha_{0n} = atan(\frac{\Delta y}{\Delta x})$
$\alpha_{01} = atan(\frac{3}{1})= 1,249 = 71,6°$
$\alpha_{02} = atan(\frac{4}{3})= 0,927 = 53,1°$
$\alpha_{03} = atan(\frac{0}{3})= 0= 0°$
Dann ergeben sich die zerlegten Kräfte zu:
\begin{align*} F_{x,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{x,0n} = F_{0n} \cdot sin(\alpha_{0n}) \\ F_{x,0} &= (-5N) \cdot sin(71,6°) + (-6N) \cdot sin(53,1°) + (+3N) \cdot sin(0°) \\ F_{x,0} &= -2,18 N \\ \\ F_{y,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{y,0n} = F_{0n} \cdot cos(\alpha_{0n}) \\ F_{y,0} &= (-5N) \cdot cos(71,6°) + (-6N) \cdot cos(53,1°) + (+3N) \cdot cos(0°) \\ F_{y,0} &= -9,54 N \\ \\ \end{align*}