Exercise E6 Resistance of a Wire by Resistivity
(written test, approx. 6 % of a 60-minute written test, WS2022)
A heating element made of a Nichrome wire with a round cross-section is used in an electric oven.
Nichrome is a common Nickel Chromium alloy for heating elements.
The Nichrome wire has a resistivity of $1.10\cdot 10^{-6} ~\Omega \rm{m}$.
The heating element is $3 ~\rm{m}$ long and has a diameter of $3.57 ~\rm{mm}$.
1. Calculate the resistance $R$ of the heating element.
2. The heating element is used to heat the oven to a temperature of $180~°\rm{C}$. For this, a power dissipation (= heat flow) of $P=40 ~\rm{W}$ is necessary.
Calculate the current $I$ needed to operate it.
Exercise E1 Resistance of a Wire by Resistivity
(written test, approx. 6 % of a 60-minute written test, WS2022)
A heating element made of a Nichrome wire with a round cross-section is used in an electric oven.
Nichrome is a common Nickel Chromium alloy for heating elements.
The Nichrome wire has a resistivity of $1.10\cdot 10^{-6} ~\Omega \rm{m}$.
The heating element is $3 ~\rm{m}$ long and has a diameter of $3.57 ~\rm{mm}$.
1. Calculate the resistance $R$ of the heating element.
2. The heating element is used to heat the oven to a temperature of $180~°\rm{C}$. For this, a power dissipation (= heat flow) of $P=40 ~\rm{W}$ is necessary.
Calculate the current $I$ needed to operate it.
Exercise E2
Temperature-dependent Resistance
(written test, approx. 6 % of a 60-minute written test, WS2022)
A thermistor is used as a temperature sensor in a refrigeration system. The thermistor has a resistance of $10 ~\rm{k}\Omega$ at $+25 ~°\rm{C}$.
Its temperature coefficients are: $\alpha=0.01 ~{{1}\over{\rm{K}}}$ and $\beta=71 \cdot 10^{-6}~{{1}\over{\rm{K}^2}}$
The temperature inside the refrigeration system can reach down to $-40 ~°\rm{C}$.
1. Calculate the resistance of the thermistor at $-40 ~°\rm{C}$.
\begin{align*} R &= R_0 \cdot (1 + \alpha \cdot \Delta T + \beta \cdot \Delta T^2) && | \text{with } \Delta T = T_{\rm end} - T_{\rm start}\\ R &= 10 ~\rm{k}\Omega \cdot \left(1 + 0.01 ~{{1}\over{\rm{K}}} \cdot (-40~°\rm{C} - 25~°\rm{C} ) + 71 \cdot 10^{-6}~{{1}\over{\rm{K}^2}} \cdot (-40~°\rm{C} - 25~°\rm{C})^2 \right) \\ \end{align*}
\begin{align*} R &= 6.5 ~\rm{k}\Omega \\ \end{align*}
2. Additionally, explain which effect a resistive temperature sensor can have on the refrigeration system.
3. Regarding question 2.: Given a constant sensor voltage, would a sensor with tenfold resistance be better or worse? Give an explanation for your answer.
Therefore, with constant $U$ and increasing $R$ the power decreases. Ten times more resistance decreases the heat flow to one-tenth.
Exercise E2
Temperature-dependent Resistance
(written test, approx. 6 % of a 60-minute written test, WS2022)
A thermistor is used as a temperature sensor in a refrigeration system. The thermistor has a resistance of $10 ~\rm{k}\Omega$ at $+25 ~°\rm{C}$.
Its temperature coefficients are: $\alpha=0.01 ~{{1}\over{\rm{K}}}$ and $\beta=71 \cdot 10^{-6}~{{1}\over{\rm{K}^2}}$
The temperature inside the refrigeration system can reach down to $-40 ~°\rm{C}$.
1. Calculate the resistance of the thermistor at $-40 ~°\rm{C}$.
\begin{align*} R &= R_0 \cdot (1 + \alpha \cdot \Delta T + \beta \cdot \Delta T^2) && | \text{with } \Delta T = T_{\rm end} - T_{\rm start}\\ R &= 10 ~\rm{k}\Omega \cdot \left(1 + 0.01 ~{{1}\over{\rm{K}}} \cdot (-40~°\rm{C} - 25~°\rm{C} ) + 71 \cdot 10^{-6}~{{1}\over{\rm{K}^2}} \cdot (-40~°\rm{C} - 25~°\rm{C})^2 \right) \\ \end{align*}
\begin{align*} R &= 6.5 ~\rm{k}\Omega \\ \end{align*}
2. Additionally, explain which effect a resistive temperature sensor can have on the refrigeration system.
3. Regarding question 2.: Given a constant sensor voltage, would a sensor with tenfold resistance be better or worse? Give an explanation for your answer.
Therefore, with constant $U$ and increasing $R$ the power decreases. Ten times more resistance decreases the heat flow to one-tenth.
Exercise E8 Pure Resistor Network Simplification
(written test, approx. 13 % of a 60-minute written test, WS2022)
The following circuit with $R_1=200 ~\Omega$, $R_2=R_3=100 ~\Omega$ and the switch $S$ is given.
1. The switch shall now be open. Calculate the equivalent resistance $R_{\rm eq}$ between $\rm A$ and $\rm B$.
2. The switch shall now be closed. Calculate the equivalent resistance $R_{\rm eq}$ between $\rm A$ and $\rm B$.
The equivalent resistor is given by a parallel configuration of resistors in series: \begin{align*} R_{\rm eq} &= R_Y + (R_Y + R_1 + R_1)||(R_Y + R_2)\\ R_{\rm eq} &= 33.33 ~\Omega + (33.33 ~\Omega + 400 ~\Omega)||(33.33 ~\Omega + 100 ~\Omega)\\ \end{align*}
Exercise E3 Pure Resistor Network Simplification
(written test, approx. 13 % of a 60-minute written test, WS2022)
The following circuit with $R_1=200 ~\Omega$, $R_2=R_3=100 ~\Omega$ and the switch $S$ is given.
1. The switch shall now be open. Calculate the equivalent resistance $R_{\rm eq}$ between $\rm A$ and $\rm B$.
2. The switch shall now be closed. Calculate the equivalent resistance $R_{\rm eq}$ between $\rm A$ and $\rm B$.
The equivalent resistor is given by a parallel configuration of resistors in series: \begin{align*} R_{\rm eq} &= R_Y + (R_Y + R_1 + R_1)||(R_Y + R_2)\\ R_{\rm eq} &= 33.33 ~\Omega + (33.33 ~\Omega + 400 ~\Omega)||(33.33 ~\Omega + 100 ~\Omega)\\ \end{align*}
Exercise E1 Equivalent linear Source
(written test, approx. 14 % of a 60-minute written test, WS2022)
The circuit in the following has to be simplified.
Calculated the internal resistance $R_\rm i$ and the source voltage $U_\rm s$ of an equivalent linear voltage source on the connectors $\rm A$ and $\rm B$. \begin{align*} R_1=5.0 ~\Omega, && U_2=6.0 ~\rm{V}, && R_3= 10 ~\Omega, \\ I_4=4.2 ~\rm{A}, && R_5=10 ~\Omega , && R_6=7.5 ~\Omega, \\ R_7=15 ~\Omega && && \end{align*} Use equivalent sources in order to simplify the circuit!
The best thing is to re-think the wiring like rubber bands and adjust them:
The linear voltage source of $U_2$ and $R_1$ can be transformed into a current source $I_2={{U_2}\over{R_1}}$ and $R_1$:
Now a lot of them can be combined. The resistors $R_1$, $R_3$, $R_5$ are in parallel, like also $I_2$ and $I_4$:
\begin{align*}
R_{135} &= R_1||R_3||R_5\\
I_{24} &= I_2 - I_4 = {{U_2}\over{R_1}} - I_4
\end{align*}
The resulting circuit can again be transformed:
Here, the $U_{24}$ is calculated by $I_{24}$ as the following:
\begin{align*}
U_{24} &= R_{135} \cdot I_{24} \\
&= ({{U_2}\over{R_1}} - I_4) \cdot R_1||R_3||R_5
\end{align*}
On the right side of the last circuit, there is a voltage divider given by $R_{135}$, $R_6$, and $R_7$.
Therefore the voltage between $A$ and $B$ is given as:
\begin{align*}
U_{\rm AB} &= U_{24} \cdot {{R_7}\over{R_6 + R_7 + R_1||R_3||R_5}} \\
&= ({{U_2}\over{R_1}} - I_4) \cdot {{R_7 \cdot R_1||R_3||R_5}\over{R_6 + R_7 + R_1||R_3||R_5}} \\
\end{align*}
For the internal resistance $R_i$ the ideal voltage source is substituted by its resistance ($=0\Omega$, so a short-circuit): \begin{align*} R_{\rm AB} &= R_7 || ( R_6 + R_1||R_3||R_5) \\ \end{align*}
with $R_1||R_3||R_5 = 5 ~\Omega || 10 ~\Omega || 10 ~\Omega = 5 ~\Omega || 5 ~\Omega = 2.5 ~\Omega$:
\begin{align*} U_{\rm AB} &= ({{6.0 ~\rm{V}}\over{5.0 ~\Omega}} - 4.2 ~\Omega) \cdot {{15 ~\Omega \cdot 2.5 ~\Omega}\over{7.5 ~\Omega + 15 ~\Omega + 2.5 ~\Omega}} \\ R_{\rm AB} &= 15 ~\Omega|| ( 7.5 ~\Omega + 2.5 ~\Omega) \\ \end{align*}
Exercise E4 Equivalent linear Source
(written test, approx. 14 % of a 60-minute written test, WS2022)
The circuit in the following has to be simplified.
Calculated the internal resistance $R_\rm i$ and the source voltage $U_\rm s$ of an equivalent linear voltage source on the connectors $\rm A$ and $\rm B$. \begin{align*} R_1=5.0 ~\Omega, && U_2=6.0 ~\rm{V}, && R_3= 10 ~\Omega, \\ I_4=4.2 ~\rm{A}, && R_5=10 ~\Omega , && R_6=7.5 ~\Omega, \\ R_7=15 ~\Omega && && \end{align*} Use equivalent sources in order to simplify the circuit!
The best thing is to re-think the wiring like rubber bands and adjust them:
The linear voltage source of $U_2$ and $R_1$ can be transformed into a current source $I_2={{U_2}\over{R_1}}$ and $R_1$:
Now a lot of them can be combined. The resistors $R_1$, $R_3$, $R_5$ are in parallel, like also $I_2$ and $I_4$:
\begin{align*}
R_{135} &= R_1||R_3||R_5\\
I_{24} &= I_2 - I_4 = {{U_2}\over{R_1}} - I_4
\end{align*}
The resulting circuit can again be transformed:
Here, the $U_{24}$ is calculated by $I_{24}$ as the following:
\begin{align*}
U_{24} &= R_{135} \cdot I_{24} \\
&= ({{U_2}\over{R_1}} - I_4) \cdot R_1||R_3||R_5
\end{align*}
On the right side of the last circuit, there is a voltage divider given by $R_{135}$, $R_6$, and $R_7$.
Therefore the voltage between $A$ and $B$ is given as:
\begin{align*}
U_{\rm AB} &= U_{24} \cdot {{R_7}\over{R_6 + R_7 + R_1||R_3||R_5}} \\
&= ({{U_2}\over{R_1}} - I_4) \cdot {{R_7 \cdot R_1||R_3||R_5}\over{R_6 + R_7 + R_1||R_3||R_5}} \\
\end{align*}
For the internal resistance $R_i$ the ideal voltage source is substituted by its resistance ($=0\Omega$, so a short-circuit): \begin{align*} R_{\rm AB} &= R_7 || ( R_6 + R_1||R_3||R_5) \\ \end{align*}
with $R_1||R_3||R_5 = 5 ~\Omega || 10 ~\Omega || 10 ~\Omega = 5 ~\Omega || 5 ~\Omega = 2.5 ~\Omega$:
\begin{align*} U_{\rm AB} &= ({{6.0 ~\rm{V}}\over{5.0 ~\Omega}} - 4.2 ~\Omega) \cdot {{15 ~\Omega \cdot 2.5 ~\Omega}\over{7.5 ~\Omega + 15 ~\Omega + 2.5 ~\Omega}} \\ R_{\rm AB} &= 15 ~\Omega|| ( 7.5 ~\Omega + 2.5 ~\Omega) \\ \end{align*}
Exercise E7
Charging Capacitors
(written test, approx. 16 % of a 60-minute written test, WS2022)
The circuit shown in the following is used to control the brightness when turning on a small light bulb.
The circuit contains a voltage source $U=12 ~\rm{V}$, a switch $S_1$, a resistor of $R_1=20 ~\Omega$ and a capacitor of $C=100 ~\rm{µF}$.
The switch $S_2$ to an additional consumer $R_2$ will be considered to be open for the first tasks. At the moment $t_0=0 ~\rm{s}$ the switch $S_1$ is closed, the voltage across the capacitor is $u_c (t_0 )=0 ~\rm{V}$.
1. First do not consider the light bulb – it is not connected to the RC circuit.
Calculate the point of time $t_1$ when $u_c (t_1)=0.5\cdot U$.
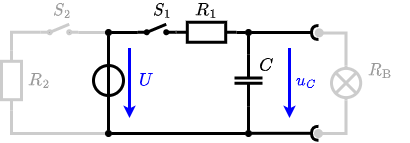
So, here only R_1 and C gives the time constant: $\tau = R_1 \cdot C$
The following formula describes the time course of $u_C(t)$ which has to be $u_c (t_1)=0.5\cdot U$: \begin{align*} u_c (t) = U \cdot (1- e^{t/\tau}) = 0.5\cdot U \end{align*} It has to be rearranged to $t$ \begin{align*} (1- e^{t/\tau}) &= 0.5 \\ e^{t/\tau} &= 0.5 \\ t/\tau &= ln(0.5) \\ t &= \tau \cdot ln(0.5) \\ t &= R_1 \cdot C \cdot ln(0.5) \end{align*}
2. Calculate the overall energy dissipated by $R_1$ while charging the capacitor $0 ~\rm{V}$ to $12 ~\rm{V}$.
3. Now, consider the light bulb as a resistor of $R_\rm B=20 ~\Omega$, and ignore again the left side ($S_2$ is open).
The voltage across the capacitor is again $0 ~\rm{V}$ at the moment $t_0=0 ~\rm{s}$ when the switch $S_1$ is closed.
Calculate the voltage $u_c (t_2)$ across the capacitor at $t_2=1 ~\rm{ms}$ after closing the switch.
Hint: To solve this, first create an equivalent linear voltage source from $U$, $R_1$, and $R_\rm B$.
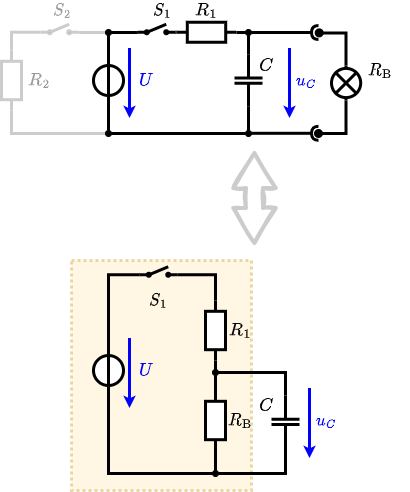
An equivalent linear voltage source can be given with $U$, $R_1$, and $R_\rm B$ as seen in yellow.
Therefore, the voltage of the equivalent linear voltage source is: $U_s = U \cdot {{R_\rm B}\over{R_1 + R_\rm B}} = 1/2 \cdot U$
The internal resistance is given by substituting the ideal voltage source with its resistance ($=0 ~\Omega$, short-circuit).
\begin{align*}
R_i &= R_1 || R_\rm B \\
&= 10 ~\Omega
\end{align*}
\begin{align*} u_c (t_2) &= U_s \cdot (1- e^{t_2/(R_i\cdot C)}) \\ &= {{1}\over{2}} \cdot U \cdot (1- e^{1~\rm{ms}/(10 ~\Omega \cdot 100 ~\rm{µF})}) \end{align*}
4. Explain (without calculation) how the situation in 3. would change once also $S_2$ is closed from the beginning on.
On an alternative view, one can try to create an equivalent linear voltage source again. Then, the internal resistance is given by substituting the ideal voltage source is again short-circuiting $R_2$.
Exercise E5
Charging Capacitors
(written test, approx. 16 % of a 60-minute written test, WS2022)
The circuit shown in the following is used to control the brightness when turning on a small light bulb.
The circuit contains a voltage source $U=12 ~\rm{V}$, a switch $S_1$, a resistor of $R_1=20 ~\Omega$ and a capacitor of $C=100 ~\rm{µF}$.
The switch $S_2$ to an additional consumer $R_2$ will be considered to be open for the first tasks. At the moment $t_0=0 ~\rm{s}$ the switch $S_1$ is closed, the voltage across the capacitor is $u_c (t_0 )=0 ~\rm{V}$.
1. First do not consider the light bulb – it is not connected to the RC circuit.
Calculate the point of time $t_1$ when $u_c (t_1)=0.5\cdot U$.

So, here only R_1 and C gives the time constant: $\tau = R_1 \cdot C$
The following formula describes the time course of $u_C(t)$ which has to be $u_c (t_1)=0.5\cdot U$: \begin{align*} u_c (t) = U \cdot (1- e^{t/\tau}) = 0.5\cdot U \end{align*} It has to be rearranged to $t$ \begin{align*} (1- e^{t/\tau}) &= 0.5 \\ e^{t/\tau} &= 0.5 \\ t/\tau &= ln(0.5) \\ t &= \tau \cdot ln(0.5) \\ t &= R_1 \cdot C \cdot ln(0.5) \end{align*}
2. Calculate the overall energy dissipated by $R_1$ while charging the capacitor $0 ~\rm{V}$ to $12 ~\rm{V}$.
3. Now, consider the light bulb as a resistor of $R_\rm B=20 ~\Omega$, and ignore again the left side ($S_2$ is open).
The voltage across the capacitor is again $0 ~\rm{V}$ at the moment $t_0=0 ~\rm{s}$ when the switch $S_1$ is closed.
Calculate the voltage $u_c (t_2)$ across the capacitor at $t_2=1 ~\rm{ms}$ after closing the switch.
Hint: To solve this, first create an equivalent linear voltage source from $U$, $R_1$, and $R_\rm B$.

An equivalent linear voltage source can be given with $U$, $R_1$, and $R_\rm B$ as seen in yellow.
Therefore, the voltage of the equivalent linear voltage source is: $U_s = U \cdot {{R_\rm B}\over{R_1 + R_\rm B}} = 1/2 \cdot U$
The internal resistance is given by substituting the ideal voltage source with its resistance ($=0 ~\Omega$, short-circuit).
\begin{align*}
R_i &= R_1 || R_\rm B \\
&= 10 ~\Omega
\end{align*}
\begin{align*} u_c (t_2) &= U_s \cdot (1- e^{t_2/(R_i\cdot C)}) \\ &= {{1}\over{2}} \cdot U \cdot (1- e^{1~\rm{ms}/(10 ~\Omega \cdot 100 ~\rm{µF})}) \end{align*}
4. Explain (without calculation) how the situation in 3. would change once also $S_2$ is closed from the beginning on.
On an alternative view, one can try to create an equivalent linear voltage source again. Then, the internal resistance is given by substituting the ideal voltage source is again short-circuiting $R_2$.
Exercise E3 Analyzing complex Impedances
(written test, approx. 14 % of a 60-minute written test, WS2022)
A circuit with an ideal voltage source ($U=50 ~\rm V$, $f=330 ~\rm Hz$) and two components ($R$ and $\underline{X}_1$) shall be given.
After analysis, the following formula for the impedance was extracted:
\begin{align*}
\underline{Z} = \left({{2}\over{3+4{\rm j}}}+5{\rm j} \right) \Omega
\end{align*}
1. Calculate the physical values of the two components.
\begin{align*} \underline{Z} &= \left({{2}\over{3+4{\rm j}}} + 5{\rm j} \right) ~\Omega \\ &= \left({{2}\over{3+4{\rm j}}} \cdot {{3-4{\rm j}}\over{3-4j}} + 5{\rm j} \right) ~\Omega \\ &= \left({{2}\over{9+16 }} \cdot (3-4{\rm j} ) + 5{\rm j} \right) ~\Omega \\ &= \left(0.24 - 0.32{\rm j} + 5{\rm j} \right) ~\Omega \\ &= 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega \\ &= R + {\rm j} X_L \\ \end{align*}
With the complex part comes the physical value: \begin{align*} X_L &= \omega L \\ L &= {{X_L}\over{2\pi \cdot f}} \\ &= {{4.68 ~\Omega}\over{2\pi \cdot 300 ~\rm{Hz}}} \\ \end{align*}
\begin{align*} R &= 0.24 ~\Omega \\ L &= 2.26 ~\rm{mH} \end{align*}
2. Calculate the phase and absolute value of complex current $\underline{I}$ through the circuit.
\begin{align*} \underline{I} &= {{\underline{U}}\over{\underline{Z}}} \\ &= {{50 ~\rm{V}}\over{ 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega }} \\ &= {{50 ~\rm{V}}\over{ 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega }} \cdot {{ 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega }\over{ 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega }} \\ &= {{50 ~\rm{V}}\over{(0.24 ~\Omega)^2 + (4.68 ~\Omega)^2 }} \cdot ( 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega ) \\ \end{align*}
The absolute value $|\underline{I}|$ can be calculated as: \begin{align*} |\underline{I}| &= {|{\underline{U}|}\over{|\underline{Z}|}} \\ &= {{50 ~\rm{V}}\over{| 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega |}} \\ &= {{50 ~\rm{V}}\over{\sqrt{ (0.24 ~\Omega)^2 + (4.68 ~\Omega)^2 }}} \end{align*}
The phase $\varphi_i$ can be calculated as \begin{align*} \varphi_i &= \arctan \left( {{\Im()}\over{\Re()}} \right) \\ &= \arctan \left( {{-4.68 ~\Omega}\over{0.24 ~\Omega}} \right) \\ \end{align*}
\begin{align*} |\underline{I}| &= 10.67 ~\rm{A} \\ \varphi_i &= -87.06° \end{align*}
3. Now an additional component $\underline{X}_2$ shall be added in series to the two components.
This component shall be dimensioned in such a way that the current and voltage are in phase. Calculate these component value!
Therefore, the component mus be a capacitor with the same absolute value of impedance: $|\underline{X}_C| = |\underline{X}_L| $ \begin{align*} X_C &= {{1}\over{\omega \cdot C}} = X_L \\ C &= {{1}\over{\omega \cdot X_L}} \\ &= {{1}\over{2\pi \cdot 300 ~\rm{Hz} \cdot 4.68 ~\Omega}} \\ \end{align*}
Exercise E6 Analyzing complex Impedances
(written test, approx. 14 % of a 60-minute written test, WS2022)
A circuit with an ideal voltage source ($U=50 ~\rm V$, $f=330 ~\rm Hz$) and two components ($R$ and $\underline{X}_1$) shall be given.
After analysis, the following formula for the impedance was extracted:
\begin{align*}
\underline{Z} = \left({{2}\over{3+4{\rm j}}}+5{\rm j} \right) \Omega
\end{align*}
1. Calculate the physical values of the two components.
\begin{align*} \underline{Z} &= \left({{2}\over{3+4{\rm j}}} + 5{\rm j} \right) ~\Omega \\ &= \left({{2}\over{3+4{\rm j}}} \cdot {{3-4{\rm j}}\over{3-4j}} + 5{\rm j} \right) ~\Omega \\ &= \left({{2}\over{9+16 }} \cdot (3-4{\rm j} ) + 5{\rm j} \right) ~\Omega \\ &= \left(0.24 - 0.32{\rm j} + 5{\rm j} \right) ~\Omega \\ &= 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega \\ &= R + {\rm j} X_L \\ \end{align*}
With the complex part comes the physical value: \begin{align*} X_L &= \omega L \\ L &= {{X_L}\over{2\pi \cdot f}} \\ &= {{4.68 ~\Omega}\over{2\pi \cdot 300 ~\rm{Hz}}} \\ \end{align*}
\begin{align*} R &= 0.24 ~\Omega \\ L &= 2.26 ~\rm{mH} \end{align*}
2. Calculate the phase and absolute value of complex current $\underline{I}$ through the circuit.
\begin{align*} \underline{I} &= {{\underline{U}}\over{\underline{Z}}} \\ &= {{50 ~\rm{V}}\over{ 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega }} \\ &= {{50 ~\rm{V}}\over{ 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega }} \cdot {{ 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega }\over{ 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega }} \\ &= {{50 ~\rm{V}}\over{(0.24 ~\Omega)^2 + (4.68 ~\Omega)^2 }} \cdot ( 0.24 ~\Omega - {\rm j} \cdot 4.68 ~\Omega ) \\ \end{align*}
The absolute value $|\underline{I}|$ can be calculated as: \begin{align*} |\underline{I}| &= {|{\underline{U}|}\over{|\underline{Z}|}} \\ &= {{50 ~\rm{V}}\over{| 0.24 ~\Omega + {\rm j} \cdot 4.68 ~\Omega |}} \\ &= {{50 ~\rm{V}}\over{\sqrt{ (0.24 ~\Omega)^2 + (4.68 ~\Omega)^2 }}} \end{align*}
The phase $\varphi_i$ can be calculated as \begin{align*} \varphi_i &= \arctan \left( {{\Im()}\over{\Re()}} \right) \\ &= \arctan \left( {{-4.68 ~\Omega}\over{0.24 ~\Omega}} \right) \\ \end{align*}
\begin{align*} |\underline{I}| &= 10.67 ~\rm{A} \\ \varphi_i &= -87.06° \end{align*}
3. Now an additional component $\underline{X}_2$ shall be added in series to the two components.
This component shall be dimensioned in such a way that the current and voltage are in phase. Calculate these component value!
Therefore, the component mus be a capacitor with the same absolute value of impedance: $|\underline{X}_C| = |\underline{X}_L| $ \begin{align*} X_C &= {{1}\over{\omega \cdot C}} = X_L \\ C &= {{1}\over{\omega \cdot X_L}} \\ &= {{1}\over{2\pi \cdot 300 ~\rm{Hz} \cdot 4.68 ~\Omega}} \\ \end{align*}
Exercise E5 Impedances at different Frequencies
(written test, approx. 18 % of a 60-minute written test, WS2022)
Calculate the resistor values which have to be used in the following circuits.
1. A resistor $R_1$ shall have the same absolute value of the impedance as a capacitor $C_1=40 ~{\rm nF}$ at $f_1=4 ~{\rm MHz}$.
\begin{align*} R_1 &= |\underline{X}_{C1}| \\ &= {{1}\over{2\pi \cdot f \cdot C_1}} \\ &= {{1}\over{2\pi \cdot 4 ~{\rm MHz} \cdot 40 ~\rm nF}} \\ \end{align*}
2. A $RL$ series circuit with $L_2=4.7 ~\rm µH$, where an AC voltage source of $U_2=1.0 ~\rm V$ with $f_2=450 ~\rm kHz$ generates a current $I_2=60 ~\rm mA$.
The equivalent impedance for $R$ and $L$ combined is given by \begin{align*} {{\underline{U}}\over{\underline{I}}} &= R_2 + \underline{X}_{L2} \\ &= R_2 + {\rm j} \cdot \omega L \end{align*} Since ${\rm j} \cdot \omega L $ is perpendicular to $R_2$ this can be simplified to: \begin{align*} \left| {{\underline{U}}\over{\underline{I}}} \right|^2 &= |R_2|^2 + |\underline{X}_{L2}|^2 \\ \left( {{U}\over{I}} \right)^2 &= {R_2}^2 + {X_{L2}}^2 \\ \end{align*}
This can be rearranged to get $R_2$: \begin{align*} R_2 &= \sqrt{ \left( {{U }\over{I }} \right)^2 - X_{L2}^2 } \\ &= \sqrt{ \left( {{1~{\rm V}}\over{60~\rm mA}} \right)^2 - (2\pi \cdot 450~{\rm kHz} \cdot 4.7 ~ {\rm µH})^2 } \\ \end{align*}
\begin{align*} R_2 &= 10.0 ~\Omega \\ \end{align*}
3. A $RC$ parallel circuit with $C_3=4.7 ~\rm nF$ on an AC current source ($I_{3S}=1.3 ~\rm A$,$f_3=200 ~\rm kHz$), which generates a current of $I_{3R}=1.0 ~\rm A$ through $R_3$.
Parallel circuit means that the voltage is the same on $R_3$ and $C_3$:
\begin{align*}
\underline{U}_3 = R_3 \cdot \underline{I}_{3R} = -{\rm j}\cdot {X}_{3C} \cdot \underline{I}_{3C}
\end{align*}
So it gets clear, that $\underline{I}_{3R}$ is perpendicular to $\underline{I}_{3C}$ (It has to, since $R_3$ is perpendicular to $-{\rm j}\cdot {X}_{3C}$, too).
Therefore, the resulting current of the parallel circuit is given as:
\begin{align*}
\underline{I}_{3} &= \underline{I}_{3R} + \underline{I}_{3C} \\
|\underline{I}_{3}|^2 &= |\underline{I}_{3R}|^2 + |\underline{I}_{3C}|^2 \\
{I}_{3C} &= \sqrt{|{I}_{3}|^2 - |{I}_{3R}|^2}
\end{align*}
Back to the first formula: \begin{align*} R_3 \cdot {I}_{3R} &= {X}_{3C} \cdot {I}_{3C} \\ R_3 &= {X}_{3C} \cdot {{{I}_{3C}}\over{{I}_{3R}}} \\ &= {{1}\over{2\pi \cdot f \cdot C_3}} \cdot {{\sqrt{|{I}_{3}|^2 - |{I}_{3R}|^2}}\over{{I}_{3R}}} \\ \end{align*}
\begin{align*} R_3 &= 70.0 ~\Omega \\ \end{align*}
Exercise E7 Impedances at different Frequencies
(written test, approx. 18 % of a 60-minute written test, WS2022)
Calculate the resistor values which have to be used in the following circuits.
1. A resistor $R_1$ shall have the same absolute value of the impedance as a capacitor $C_1=40 ~{\rm nF}$ at $f_1=4 ~{\rm MHz}$.
\begin{align*} R_1 &= |\underline{X}_{C1}| \\ &= {{1}\over{2\pi \cdot f \cdot C_1}} \\ &= {{1}\over{2\pi \cdot 4 ~{\rm MHz} \cdot 40 ~\rm nF}} \\ \end{align*}
2. A $RL$ series circuit with $L_2=4.7 ~\rm µH$, where an AC voltage source of $U_2=1.0 ~\rm V$ with $f_2=450 ~\rm kHz$ generates a current $I_2=60 ~\rm mA$.
The equivalent impedance for $R$ and $L$ combined is given by \begin{align*} {{\underline{U}}\over{\underline{I}}} &= R_2 + \underline{X}_{L2} \\ &= R_2 + {\rm j} \cdot \omega L \end{align*} Since ${\rm j} \cdot \omega L $ is perpendicular to $R_2$ this can be simplified to: \begin{align*} \left| {{\underline{U}}\over{\underline{I}}} \right|^2 &= |R_2|^2 + |\underline{X}_{L2}|^2 \\ \left( {{U}\over{I}} \right)^2 &= {R_2}^2 + {X_{L2}}^2 \\ \end{align*}
This can be rearranged to get $R_2$: \begin{align*} R_2 &= \sqrt{ \left( {{U }\over{I }} \right)^2 - X_{L2}^2 } \\ &= \sqrt{ \left( {{1~{\rm V}}\over{60~\rm mA}} \right)^2 - (2\pi \cdot 450~{\rm kHz} \cdot 4.7 ~ {\rm µH})^2 } \\ \end{align*}
\begin{align*} R_2 &= 10.0 ~\Omega \\ \end{align*}
3. A $RC$ parallel circuit with $C_3=4.7 ~\rm nF$ on an AC current source ($I_{3S}=1.3 ~\rm A$,$f_3=200 ~\rm kHz$), which generates a current of $I_{3R}=1.0 ~\rm A$ through $R_3$.
Parallel circuit means that the voltage is the same on $R_3$ and $C_3$:
\begin{align*}
\underline{U}_3 = R_3 \cdot \underline{I}_{3R} = -{\rm j}\cdot {X}_{3C} \cdot \underline{I}_{3C}
\end{align*}
So it gets clear, that $\underline{I}_{3R}$ is perpendicular to $\underline{I}_{3C}$ (It has to, since $R_3$ is perpendicular to $-{\rm j}\cdot {X}_{3C}$, too).
Therefore, the resulting current of the parallel circuit is given as:
\begin{align*}
\underline{I}_{3} &= \underline{I}_{3R} + \underline{I}_{3C} \\
|\underline{I}_{3}|^2 &= |\underline{I}_{3R}|^2 + |\underline{I}_{3C}|^2 \\
{I}_{3C} &= \sqrt{|{I}_{3}|^2 - |{I}_{3R}|^2}
\end{align*}
Back to the first formula: \begin{align*} R_3 \cdot {I}_{3R} &= {X}_{3C} \cdot {I}_{3C} \\ R_3 &= {X}_{3C} \cdot {{{I}_{3C}}\over{{I}_{3R}}} \\ &= {{1}\over{2\pi \cdot f \cdot C_3}} \cdot {{\sqrt{|{I}_{3}|^2 - |{I}_{3R}|^2}}\over{{I}_{3R}}} \\ \end{align*}
\begin{align*} R_3 &= 70.0 ~\Omega \\ \end{align*}
Exercise E4 Complex Impedance Circuit
(written test, approx. 15 % of a 60-minute written test, WS2022)
A circuit designed to filter the noise from a signal shall be analyzed.
The input is given by a voltage source $u(t) = 3.0 ~{\rm V} \cdot \sin(2\pi \cdot 15 ~{\rm kHz} \cdot t)$ with an internal resistance of $10 ~\Omega$.
This linear source is connected with an inductor of $330 ~ {\rm µH}$ and a capacitor of $0.22 ~{\rm µF}$, all in series.
1. Draw the circuit diagram of the given circuit.
Label all components, voltages, and currents.
2. Calculate the single impedance $|\underline{Z}_C|$, $|\underline{Z}_L|$ such as $|\underline{Z}|$ of the overall circuit.
\begin{align*} Z_C &= {{1}\over{2\pi \cdot f \cdot C}}\\ &= {{1}\over{2\pi \cdot 15 ~{\rm kHz} \cdot 0.22 ~{\rm µF}}}\\ \end{align*}
\begin{align*} Z_L &= 2\pi \cdot f \cdot L\\ &= 2\pi \cdot 15 ~{\rm kHz} \cdot 0.22 ~{\rm µF}\\ \end{align*}
\begin{align*} Z_C &= {{1}\over{2\pi \cdot f \cdot C}}\\ &= {{1}\over{2\pi \cdot 15 ~{\rm kHz} \cdot 330 ~{\rm µH}}}\\ \end{align*}
\begin{align*} \underline{Z} &= R + \underline{Z}_L + \underline{Z}_C \\ &= R + j \cdot {Z}_L - j \cdot {Z}_C \\ &= R + j \cdot ({Z}_L - {Z}_C) \\ |\underline{Z}| &= \sqrt{R^2 + (\underline{Z}_L - \underline{Z}_C)^2 }\\ \end{align*}
\begin{align*} Z_L &= 31.1 ~\Omega \\ Z_C &= 48.2 ~\Omega \\ Z &= 19.8 ~\Omega \end{align*}
3. Draw the three impedance phasors $|\underline{Z}_C|$, $|\underline{Z}_L|$ and $|\underline{Z}_R|$ in a diagram.
Choose an appropriate scaling factor and write it down.
4. Calculate the current $|\underline{I}|$.
\begin{align*} Z &= {{\hat{U}}\over{\hat{I}}} \\ \hat{I} &= {{\hat{U}}\over{Z}} \\ \end{align*}
With $I = {{1}\over{\sqrt{2}}}\cdot \hat{I}$: \begin{align*} I &= {{1}\over{\sqrt{2}}}\cdot {{\hat{U}}\over{Z}} \\ &= {{1}\over{\sqrt{2}}}\cdot {{3.0 ~{\rm V}}\over{19.28 ~\Omega}} \\ \end{align*}
\begin{align*} I = 107 ~{\rm mA} \end{align*}
Exercise E8 Complex Impedance Circuit
(written test, approx. 15 % of a 60-minute written test, WS2022)
A circuit designed to filter the noise from a signal shall be analyzed.
The input is given by a voltage source $u(t) = 3.0 ~{\rm V} \cdot \sin(2\pi \cdot 15 ~{\rm kHz} \cdot t)$ with an internal resistance of $10 ~\Omega$.
This linear source is connected with an inductor of $330 ~ {\rm µH}$ and a capacitor of $0.22 ~{\rm µF}$, all in series.
1. Draw the circuit diagram of the given circuit.
Label all components, voltages, and currents.
2. Calculate the single impedance $|\underline{Z}_C|$, $|\underline{Z}_L|$ such as $|\underline{Z}|$ of the overall circuit.
\begin{align*} Z_C &= {{1}\over{2\pi \cdot f \cdot C}}\\ &= {{1}\over{2\pi \cdot 15 ~{\rm kHz} \cdot 0.22 ~{\rm µF}}}\\ \end{align*}
\begin{align*} Z_L &= 2\pi \cdot f \cdot L\\ &= 2\pi \cdot 15 ~{\rm kHz} \cdot 0.22 ~{\rm µF}\\ \end{align*}
\begin{align*} Z_C &= {{1}\over{2\pi \cdot f \cdot C}}\\ &= {{1}\over{2\pi \cdot 15 ~{\rm kHz} \cdot 330 ~{\rm µH}}}\\ \end{align*}
\begin{align*} \underline{Z} &= R + \underline{Z}_L + \underline{Z}_C \\ &= R + j \cdot {Z}_L - j \cdot {Z}_C \\ &= R + j \cdot ({Z}_L - {Z}_C) \\ |\underline{Z}| &= \sqrt{R^2 + (\underline{Z}_L - \underline{Z}_C)^2 }\\ \end{align*}
\begin{align*} Z_L &= 31.1 ~\Omega \\ Z_C &= 48.2 ~\Omega \\ Z &= 19.8 ~\Omega \end{align*}
3. Draw the three impedance phasors $|\underline{Z}_C|$, $|\underline{Z}_L|$ and $|\underline{Z}_R|$ in a diagram.
Choose an appropriate scaling factor and write it down.
4. Calculate the current $|\underline{I}|$.
\begin{align*} Z &= {{\hat{U}}\over{\hat{I}}} \\ \hat{I} &= {{\hat{U}}\over{Z}} \\ \end{align*}
With $I = {{1}\over{\sqrt{2}}}\cdot \hat{I}$: \begin{align*} I &= {{1}\over{\sqrt{2}}}\cdot {{\hat{U}}\over{Z}} \\ &= {{1}\over{\sqrt{2}}}\cdot {{3.0 ~{\rm V}}\over{19.28 ~\Omega}} \\ \end{align*}
\begin{align*} I = 107 ~{\rm mA} \end{align*}