Inhaltsverzeichnis
1 Amplifier Basics
1.0 What is Circuit Design?
Circuit design encompasses various subfields of electronics. Abbildung 1 shows the basics of electronics, its specializations, and the interfaces.
In the subject Introduction to digital Systems digital technology with gates and various simple programmable circuits have already been described. In Electrical Engineering 1 the foundations for simple electrical components and circuits were laid.
Circuit design now concentrates on electronic components and their circuits that affect analog electronics.
These components and circuits often connect the digital with the analog world or adjust voltages and currents for other sub-circuits. In addition, the components „transistor (TRANSfer ResISTOR)“ and „diode“ form the basis for both digital, power, and high-frequency electronics. Without exaggerating, these components are the basis of the modern world; today they form the heart of every computer and microcontroller.
Circuit Design and Electronics
But what is the difference between electronics and electrical engineering? And what does electronic circuit design mean?
For this purpose, it is useful to take a closer look at the individual parts of the term „electronic circuit design“:
The German wording for „circuit design“ is „Schaltungstechnik“. The word „Technik“ here is derived from the Greek „τέχνη“ (téchne) and means as much as art or craft. At first glance, this seems a bit surprising, since „Technik“ is rarely associated with an artistic activity such as painting. In the higher semesters, however, you will learn that understanding, for example, the arrangement of electronics (circuit design) and the application of the individual components requires trained skill and creativity. This is also true for the English „design“.
A circuit is an arrangement of electrical or electronic components to form a functioning whole or an electric circuit. We already got to know the term circuit in electrical Engineering 1.
Electronics is derived from the word electrons. This „electron engineering“ considers circuits in which an electric current or voltage is controlled by other electric signals. This means, for example, that a voltage $U_{\rm in}$ controls an output voltage $U_{\rm out}$. Physically, the two signals do not have to be electrically connected.
Is it Electronics? Some Examples
We will now examine the term electronics in more detail using various examples.
First of all, a transformer will be considered. Is this an electrical or electronic component? In a transformer, the output voltage is generated by the change in the magnetic field. The change of the magnetic field in the windings is caused by the current change on the primary side. So, there is a direct transformation (a conversion) of the signals. The transformer is not considered as an electronic component. This is due to the fact that the input signal not only provides the control but also the electric power. If this is still somewhat unclear, it helps to work intensively on this chapter and to compare the following examples.
The second example is the so-called contactor. A contactor is an electrically controlled switch. In this case, a coil closes a secondary, or output-side circuit if it is energized. There is no direct electrical connection here. The contactor is often not yet regarded as an electronic but as an electromechanical component. This component is on the border between the electronic and electrical components.
The last example to be studied in the light of electronics and electrical engineering is the electron tube. An electron tube is a vacuum vessel, with several connections. Two of the connections lead internally to one electrode each, which faces each other. These can be brought to a potential difference against each other and heated. This allows electrons to escape from the electrode and generate a current to the other electrode through the vacuum. A grid is placed between these two electrodes. If this is set to an opposite potential, the current flow can be stopped. Here, the grid potential can be used to change the current flow. The electron tube is already considered an electronic component. Nowadays the electron tube has been replaced by semiconductor components.
In this course, we only deal with semiconductor electronic components and basically with silicon as semiconductor.
1.1 Amplifier - a Black Box is going to be specified
Before the amplifier is examined in more detail in the application, the interfaces and essential characteristics are to be dealt with first.
Note!
An amplifier is a system that uses a low-power input signal to control a much higher-power output signal.
The necessary energy is taken from the power supply!
Characteristics
Mostly, when an amplifier is used, it is specifically a voltage amplifier. Accordingly, the voltage amplifier is the basis for the following explanation. However, the determined values also apply to other amplifiers. In Abbildung 2 a voltage amplifier is shown as a black box. The voltage amplifier always tries to output a given multiple of the input voltage $U_\rm I$ (in German: Eingangsspannung $U_\rm E$) at the output as output voltage $U_\rm O$ (in German: Ausgangsspannung $U_\rm A$). This „multiple“ can be determined as a ratio.
The symbol of the amplifier is a rectangle with an inserted triangle. The input terminals on the left side are marked $\rm IN+$ and $\rm IN-$. The output terminals on the right side are correspondingly labeled $\rm OUT+$ and $\rm OUT-$. The input voltage $U_\rm I$ is applied between the input terminals and the output voltage $U_{\rm O}$ is applied between the output terminals.
The signal to be amplified comes from any source on the left-hand side. Often this can be seen as an ideal (voltage) source - i.e. with internal resistance. The amplified signal is fed to a load on the right-hand side. In the simplest case, this load is an ohmic resistor.
In Abbildung 3 a simulation of an ideal amplifier is shown. The input source specifies the voltage to be amplified. The amplifier with an amplification factor of 100 has the connections for input and output voltage are drawn in. On the right side, a resistor is provided as load; this can be varied via a switch.
In the simulation some characteristics of an amplifier can be seen:
- Ideally, no current flows into the amplifier on the input side.
- The current on the output side depends on the connected load. If the load resistance is reduced with the help of the switch, the current increases. The amplifier thus tries to maintain the desired voltage.
- On the output side of the amplifier, the current can flow in either direction.
The amplifier adjusts the current so that the amplified voltage $U_A=\pm 2.5~\rm V$ can be measured at the output.
Characteristics
| Characteristic groups | # | Characteristic (deutsch) | Characteristic (english) | Formula |
|---|---|---|---|---|
| Ratios | 1 | Spannungsverstärkung $A_{\rm V}$ | Voltage Amplification $A_{\rm V}$ | $\large{A_{\rm V} =\frac{U_{\rm O}}{U_{\rm I}}}$ |
| 2 | Stromverstärkung $A_{\rm C}$ | Current Amplification $A_{\rm C}$ | $\large{A_{\rm C} =\frac{I_{\rm O}}{I_{\rm I}}}$ | |
| 3 | Übertragungswiderstand $R_{\rm ü}$ | Transfer Resistance, Transimpedance $R_{\rm T}$ | $\large{R_{\rm T} =\frac{U_{\rm O}}{I_{\rm I}}}$ | |
| 4 | Übertragungsleitwert (Steilheit) $G, S$ | Transfer Conductance, Transconductance (Slope) $S$ | $\large{G = S =\frac{I_{\rm O}}{U_{\rm I}}}$ | |
| Input/Output Resistance | 5 | Eingangswiderstand $R_{\rm E}$ | Input Resistance $R_{\rm I}$ | $\large{R_{\rm I} =\frac{U_{\rm I}}{I_{\rm I}}}$ |
| 6 | Ausgangswiderstand $R_{\rm A}$ | Output Resistance $R_{\rm O}$ | $\large{R_{\rm O} =-\frac{\Delta U_{\rm O}}{\Delta I_{\rm O}}}$ | |
| Reverse gains | 7 | Spannungsrückwirkung $A_{\rm rV}$ | Reverse Voltage Gain | $\large{A_{\rm rV} =\frac{U_{\rm I}}{U_{\rm O}}}$ |
| 8 | Stromrückwirkung $A_{\rm rC}$ | Reverse Current Gain | $\large{A_{\rm rC} =\frac{I_{\rm I}}{I_{\rm O}}}$ |
The ratios of the input and output quantities of a black box are called characteristics. A well-known parameter is, for example, the efficiency $\eta = \frac{P_{\rm O}}{P_{\rm I}}$. In the case of an amplifier, only the voltages and currents are considered as input and output quantities. Various amplifier parameters are shown in the table.
Different transmission ratios result, depending on the desired input variable and the output variable, which is to be controlled. It is important that the transmission resistance $R_\rm T$ and the transfer conductance $S$ do not correspond to any electrical component, since current and voltage are not measured at the same terminals.
When current and voltage at the same „side „are put into relation, the input resistance $\boldsymbol{R_{\rm I}}$ and the output resistance $R_\rm O$ result. From electrical engineering 1 it is known that an equivalent resistance of a system is given by the quotient of open circuit voltage $U_{\rm OC}$ and short circuit current $I_{\rm SC}$. Important: A resistor must always be considered in the passive sign convention: For a (positive) resistance value, the current and voltage arrows must be plotted in the same direction. For input resistance, this is already the case (see also Abbildung 2).
However, for output resistance $\boldsymbol{R_{\rm O}}$ (in the amplifier), the arrows of $U_\rm O$ and $I_\rm O$ are antiparallel. Therefore the fraction is a negative value. For getting a resistance value this fraction must be negated accordingly. However, for the measurement of the short-circuit current $I_{\rm O, SC}$ the output resistance is also often problematic. At the beginning of this subchapter, it was already described that the voltage amplifier always tries to output a given multiple of the input voltage $U_\rm I$ at the output as input voltage $U_\rm O$. It would also attempt to do this in the event of a short circuit. The current $I_\rm O$ would accordingly become very large. When measuring the short-circuit current $I_{\rm O, SC}$, the disproportionately increasing losses $P=R_O\cdot I_O^2$ via the output resistance could then destroy the amplifier. Thus, determining the output resistance via the quotient of $U_\rm O$ and $I_\rm O$ is not possible. Since the output resistance is assumed to be an ohmic resistance - i.e. slope in the $U$-$I$ diagram - any two (load) points on the straight line can be used to form the quotient. Specifically, when measuring the output resistance, one can measure the situation of the amplifier output with two different loads $R_{\rm L,1}$ and $R_{\rm L,2}$ and find the differences $\Delta U_{\rm O}=U_{\rm O,1}-U_{\rm O,2}$ and $\Delta I_{\rm O}=I_{\rm O,1}-I_{\rm O,2}$.
The most important characteristics of the voltage amplifier are the voltage gain $A_\rm V$, as well as the input and output resistance $R_\rm I$ and $R_\rm O$.
Equivalent Circuit Diagram
After the view on the characteristics, we try to understand the internal structure of the amplifier. Up to now, The current-voltage relationships were determined from the external view. There, an input resistance $R_\rm I$ was described on the input side of the amplifier. This is now taken into account in the equivalent circuit diagram (see Abbildung 4). Resistance was also determined on the output side. Within the black box, however, it must also be noted that the amplifier - according to its name - has to amplify the input signal. So here, besides the output resistor $R_\rm O$, also an element has to be used, which outputs the amplified voltage. 1). The voltage of the voltage source depends on the voltage applied to the input resistor $R_\rm I$. It is more precisely larger by the factor of the voltage gain $A_\rm V$.
The simulation shows a (simulated) real amplifier. The input source has a high internal resistance. This means it has a high impedance and can only supply a small amount of current. The amplifier with a gain of 100 has - besides the connections for input and output voltage - also connections for the supply voltage drawn in. On the right side, a resistor is provided as load; this can be varied via a switch.
In the simulation some properties of an amplifier can be seen:
- On the input side, a small current flows into the amplifier.
- The current on the output side depends on the connected load. If the load resistance is reduced with the help of the switch, the current increases. The amplifier thus tries to maintain the desired voltage.
- The amplifier can output current as well as absorb current.
The current on the output side flows in and out of the amplifier through the supply voltage connections. - The simulation is based on a real amplifier. This has a small deviation from the expected value $U_{\rm O}=\pm 2.5~\rm V$ at the output voltage. Part of the deviation will be described later in this chapter.
Idealized Amplifier Base Types
There are basic amplifier types depending on which input variable shall change which output variable. These are listed in the following table.
Idealized Amplifier Base Types
| # | Amplifier | Symbol | $\boldsymbol{R_\rm I}$ | $\boldsymbol{R_\rm O}$ | gain |
|---|---|---|---|---|---|
| 1 | voltage amplifier | | $ \large{\rightarrow \infty}$ | $ \large{\rightarrow 0}$ | $\large{A_{\rm V} =\frac{U_\rm O}{U_\rm I}}$ |
| 2 | current amplifier | | $ \large{\rightarrow 0}$ | $ \large{\rightarrow \infty}$ | $\large{A_{\rm C} =\frac{I_\rm O}{I_\rm I}}$ |
| 3 | current-to-voltage converter | | $ \large{\rightarrow 0}$ | $ \large{\rightarrow 0}$ | $\large{R_{\rm T} =\frac{U_\rm O}{I_\rm I}}$ |
| 4 | voltage-to-current converter | | $ \large{\rightarrow \infty}$ | $ \large{\rightarrow \infty}$ | $\large{S =\frac{I_{\rm O}}{U_{\rm I}}}$ |
As a symbol in block diagrams, a square with a diagonal is drawn for the respective basic amplifier type, which contains the corresponding formula symbol on the input and output sides.
Now the input resistance $\boldsymbol{R_\rm I}$ and output resistance $\boldsymbol{R_\rm O}$ for ideal voltage amplifiers shall be considered in more detail.
If a voltage is the input, the input resistance should load the source as little as possible so that the voltage to be measured does not drop (cf. Abbildung 4). This can also be easily checked in the simulation of the real amplifier (see above). If the resistance of the load is increased there (double-click), it approaches the input resistance of the amplifier. If the value is set to $1 ~\rm M \Omega $, the voltage drops by half. The source resistance is then equal to the input resistance of the amplifier. It is therefore important that the input resistance is as high as possible, or ideally tends towards infinity.
A similar consideration can be made for the output resistance $\boldsymbol{R_\rm O}$. If a voltage is the output parameter, the output resistor must be dimensioned in such a way that the voltage at the load does not drop at the output either. The output resistance should be as small as possible so that the voltage drop there becomes low.
Now, if the input resistances $\boldsymbol{R_\rm I}$ and output resistances $\boldsymbol{R_\rm O}$ for ideal current amplifiers are considered, a different view of the amplifier is favorable. In the Abbildung 5 the same amplifier considered so far can be seen. However, in this case, all real voltage sources are replaced by real current sources. This transformation has already been described in Electrical Engineering 1. Depending on the considered electrical quantity, one or the other real source can be advantageous.
The input and output resistance of the current amplifier shall be considered with this knowledge. On the input side, most of the input current $I_\rm I$ should flow into the amplifier. The input resistance $R_\rm I$ must accordingly tend towards zero. The maximum current should also flow out of the amplifier at the amplifier output. Here, the output resistance $R_\rm O$ must accordingly tend towards infinity so that the lowest possible current flows through it.
The following applies to current-voltage and voltage-current converters:
- The respective name is composed of input variable-output variable.
- For the input and output resistances, the respective corresponding consideration of the ideal current amplifier or voltage amplifier can be used.
1.2 Feedback
One of the fundamental principles of control engineering, digital technology, and electronics is feedback. Thus, in the introduction to digital systems, the output value of a NOR gate was already fed back to its input via detours in order to create a flip-flop. Similarly, here the output value of the ideal amplifier is to be fed back to the input. In contrast to digital systems, in control engineering and electronics a fraction (in rare cases: a multiple) of the output value is fed back.
In addition, there is another tool for control engineering, digital systems, and electronics: the block diagram or signal flow diagram. In Electrical Engineering 1, only circuit diagrams have been used so far. With circuit diagrams there is an interaction of all components due to Kirchhoff's rules, furthermore, voltage differences everywhere or current can be measured over all components.
In contrast to this is the block diagram. This shows individual blocks which link a cause with an effect. In general, no reaction of the effect on the cause is assumed. Causes and effects can be voltages or currents, which are then written on the respective connecting arrow. The block diagram does not claim to conserve energy or charge but serves to provide an overview of the effects and interrelationships. Thus Kirchhoff's rules are usually not applicable there.
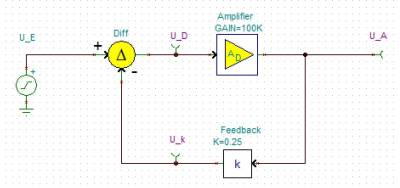
Abbildung 6 shows a block diagram of a feedback amplifier consisting of an ideal voltage amplifier with gain $A_\rm D$ drawn in the center. The output voltage $U_\rm O$, reduced by the factor $k$, is fed back via a feedback element. The circle symbol with the arithmetic symbols (in the block diagram on the left) shows how the incoming values must be offset against each other. The value $k \cdot U_\rm O$ is thus subtracted from the input value $U_\rm I$ in the indicated block diagram.
The advantage of a real amplifier in negative feedback is that the gain $A_\rm V$ of the whole system depends only negligibly on the gain factor $A_\rm D$ of the real amplifier if $A_\rm D$ is very large (see also task 1.3.2). In this case, the gain $ A_{\rm V}=\frac {1}{k}$. To avoid oscillation of the whole system, the amplifier must contain a delay element. This is present in the real amplifier in such a way that the output voltage $U_\rm O$ cannot change infinitely fast. 2) (see also task 1.3.1).
Note: feedback, positive feedback, negative feedback
Feedback (German: Rückkopplung) refers to the return of part of the output signal of an amplifier.
With positive (German: Mitkopplung) feedback, the part of the output signal with a positive sign is fed back.
The output value is therefore always increased by the input value.
With negative feedback (German: Gegenkopplung), the part of the output signal with a negative sign is fed back.
The output value therefore always attenuates the input value.
Note: Gain factors
The differential gain or open-loop gain $\boldsymbol{A_\rm D}$ (German: Differenzverstärkung) refers only to the input and output voltage of the inner amplifier: $A_{\rm D}=\frac{U_\rm O}{U_\rm D}$.
This acts only without external feedback. It is also called open-loop gain.
The voltage gain $\boldsymbol{A_\rm V}$ refers to the input and output voltage of the whole circuit with feedback: $A_{\rm V}=\frac{U_\rm O}{U_\rm I}$.
It is also called closed-loop gain.
Exercises
Exercise Sheet 1
Please upload the filled PDF in ILIAS.
Details, tips and tools for filling and inserting images can be found at:
Tools für Lehr/Lern-Veranstaltungen
| Name | First Name | Matrikelnumber |
|---|---|---|
| $\quad\quad\quad\quad\quad\quad\quad\quad$ | $\quad\quad\quad\quad\quad\quad\quad\quad$ | $\quad\quad\quad\quad\quad\quad\quad\quad$ |
| |
Exercise 1.1.1 Microphone amplifier I
An amplifier circuit shall amplify a microphone signal so that a loudspeaker ($R_{\rm LS}= 8.0 ~\Omega$) can be driven. The rms value of the desired voltage across the loudspeaker shall be $U_{\rm RMS, LS} = 10 ~\rm V$. It is assumed that a sinusoidal signal is to be output. The power is supplied by two voltage sources, with $V_{\rm S+} = 15 ~\rm V$ and $V_{\rm S-} = - 15 ~\rm V$. For understanding (especially for tasks 2. and 3.), look at the simulation under the subchapter equivalent circuit in chapter „1. amplifier basics“. This example shows a realistic amplifier, and the idealized current flow can be guessed from this.
Draw a labeled sketch of the circuit with the amplifier as a black box.
- What power (P) does the loudspeaker consume?
- From this, how can we determine the RMS current $I_{\rm RMS, S}$ of the power supply at which the above-desired voltage $U_{\rm RMS, LS}$ is output at the loudspeaker?
- Determine from the previous task the maximum current $I_{\rm max, S}$ for which the two power supplies must be designed at least.
(Note that for simple amplifiers, the output current $I_\rm O$ is always less than or equal to the current $I_\rm S$ of the power supply.)
Exercise 1.1.2 Microphone amplifier II
A voltage amplifier circuit is given, which shall amplify a microphone signal in such a way that a loudspeaker ($R_{\rm LS}= 8.0 ~\Omega$) can be driven. Neither amplification nor the desired voltage at the loudspeaker is known. This amplifier circuit is internally protected against over-currents above $I_{\rm max, amplifier}= 5.0 ~\rm A$ by a fast fuse. It is known that no over-currents occur in the allowed voltage operation of $8.0 ~\Omega$ loudspeakers.
- By what factor does the current change if a $4.0 ~\Omega$ loudspeaker is used instead of an $8.0 ~\Omega$ loudspeaker?
- What effect does this have on the fuse?
Exercise 1.1.3 Wheatstone bridge circuit
Imagine that you work in the company „HHN Mechatronics & Robotics“. You are developing an IoT system that will be used in a harsh environment and will contain a rechargeable battery. The temperature of the battery must be monitored during operation and charging. If the temperature is too high, charging must be aborted or a warning issued. For the temperature measurement at the housing of the used lithium-ion cell NCR18650 a measuring circuit is to be built up. A suggestion for the circuit is as follows:
- Wheatstone bridge circuit with $R_1 = R_2 = R_3 = R_4 = 1.0 ~\rm k \Omega $.
- Let the resistor $R_4$ be a PT1000 with a temperature coefficient $\alpha = 3850 ~\rm \frac{ppm}{K}$.
- For the other resistors, two components are chosen, that have an unknown temperature coefficient. According to the datasheet, the temperature coefficient is within $\alpha = \pm 100 ~\rm \frac{ppm}{K}$.
- The voltage source of the system generates a voltage of $5~V$ with sufficient accuracy.
- The determined voltage $\Delta U$ is amplified by a factor of 20 through another amplifier circuit, output as $U_{\rm O}$, and further used by an analog-to-digital converter in a microcontroller 1).
A short report is to be created; Tina TI is to be used as the analysis tool.
- Create a problem description.
- Rebuild the circuit in TINA TI and add this here. Take the following hint into account.
Hint
Use a simple resistor for the PT1000 in the simulation. With Tina TI, $27~°C$ (room temperature) is selected as the reference temperature for the temperature curve. For the PT1000, the reference temperature is often $0~°C$ (in practical applications, this should be checked in the datasheet). With Tina TI, the reference temperature can be changed by entering the value 27 under
Temperature [C]in the properties (double-click on Resistor).
- From the datasheet linked above, determine in what range from $T_{\rm min}$ to $T_{\rm max}$ may be charged and what temperature $T_{\rm lim}$ may not be exceeded in any of the states.
- First, for temperature invariant $R_1 = R_2 = R_3 = 1.0 ~\rm k \Omega$ and a temperature variable resistor $R_4$, determine the voltage change $\Delta U$ over the temperature of $-30...70 ~°C$ in TINA TI. To do this, create a plot with $\Delta U$ as a function of temperature.
Read $\Delta U^0 (T_{\rm min})$, $\Delta U^0 (T_{\rm max})$, $\Delta U^0 (T_{\rm lim})$, from the diagram and check the plausibility of the values by calculation.
- Determine $\Delta U$ when the temperature dependence of $R_1$, $R_2$ and $R_3$ is taken into account. To do this, create a suitable diagram with $\Delta U$ as a function of temperature in TINA TI.
At what voltages $U_O (T_{\rm min})$, $U_O (T_{\rm max})$ must the microcontroller intervene and disable charging?
At what value $U_A (T_{\rm lim})$ must a warning be issued?
- Discuss the results.
Exercise Sheet 2
Please upload the filled PDF in ILIAS.
Details, tips and tools for filling and inserting images can be found at:
Tools für Lehr/Lern-Veranstaltungen
| Name | First Name | Matrikelnumber |
|---|---|---|
| $\quad\quad\quad\quad\quad\quad\quad\quad$ | $\quad\quad\quad\quad\quad\quad\quad\quad$ | $\quad\quad\quad\quad\quad\quad\quad\quad$ |
| |
Exercise 1.2.1 Conversion of Amplifiers
In the lecture, the different amplifier types were presented as black boxes. Thereby the adjacent picture was used for the input and output quantities and the ideal resistance values were derived. In the following, you are to consider how these can be converted into each other by interconnecting them with other passive, electrical components.
How can the following amplifiers be converted into each other? For each, draw a circuit with the amplifier as shown opposite as a black box.
- Voltage amplifier into current voltage converter
- Current amplifier in voltage current converter
Exercise 1.3.1 Feedback in TINA
The TINA simulation is generally used to simulate circuit diagrams. In the following, a block diagram of the feedback (see picture) is to be examined. Please download the following file and work on the task contained in it.
file: exercise_1.3.1.tsc
Compare the results with the findings from the chapter feedback!
Exercise 1.3.2 Calculations for negative feedback
For the principle of negative feedback, the adjacent block diagram was given in the script. Here $A_\rm D$ is the so-called differential gain, i.e. the gain of the difference between the input voltage $U_\rm I$ and the feedback voltage.
- Derive the voltage gain $A_\rm V$ as a function of the differential gain $A_\rm D$ and the feedback factor $k$. Note that $A_{\rm V} = {{U_\rm O}\over{U_\rm I}} = f(A_{\rm D}, k)$ and give the derivation.
- What is the voltage gain $A_\rm V$ for an ideal differential gain ($A_\rm D \rightarrow \infty $)?
- Find the voltage gain $A_\rm V$ for feedback $k = 0.001$ with differential gain $A_{\rm D1} = 100'000$ and $A_{\rm D2} = 200'000$.
Real differential amplifiers, more precisely operational amplifiers, are considered in more detail in Chapter 3. Two operational amplifiers of the same type can have noticeably different values in the differential gain, e.g., due to specimen scattering, aging, or temperature drift.
Looking at the result from $A_{\rm D1}$ and $A_{\rm D2}$, what can be said about such a variation of a large differential gain value by, say, $50~\%$?
- State how the voltage gain behaves for the following feedback parameter $k$ with an ideal differential gain and correctly assign the following statements (some are not needed, some are needed more than once):
(A) Positive feedback,
(B) Negative feedback,
(C) Damping,
(D) gain,
(E) voltage gain equals open-loop gain,
(F) $U_{\rm O} = U_{\rm I}$,
(G) $U_{\rm O} = - U_{\rm I}$,
(H) gain equal 0.
- $k < -0$
- $k = 0$
- $0 < k < 1$
- $k = 1$
- $k > 1$
Learning Questions
for your Self-Study
- What is the definition of an amplifier?
- Explain with an example what is the essence of an amplifier.
- How do you determine the input and output resistance of an amplifier?
- How should the input and output resistance be selected for a current amplifier? Why?
- When is it called positive feedback and when is it called negative feedback?
- Explain the principle of negative feedback.
- What is the difference between voltage gain and differential gain? Briefly describe the difference between $A_\rm V$ and $A_\rm D$.
- How does $A_\rm D$ affect the output voltage $U_\rm O$ when there is no feedback in an op-amp circuit?
- What is the effect of $A_\rm D$ on the output voltage $U_\rm O$ when feedback is present in an op-amp circuit and $A_\rm D$ is increased from $100'000$ to $200'000$?
- At what value for k does the feedback become maximum?
- What values can k take for a passive feedback amplifier?
- What effect does k have on the amplifier?
- What happens if you feed back the entire output voltage?
with Answers
Only necessary to eliminate the score bar…
Exercise - Quiz
Exercise - Quiz
Exercise - Quiz
Exercise - Quiz
Exercise - Quiz