Inhaltsverzeichnis
3. Grundschaltungen
Aufgabe 3.3.1 Analyse der Impedanzwandler-Schaltung mit unterschiedlichen Operationsverstärkern
Aufgabe 3.3.1 Analyse der Impedanzwandler-Schaltung mit unterschiedlichen Operationsverstärkern
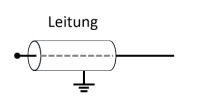
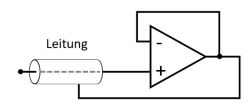
Stellen Sie sich vor, dass Sie in der Firma „HHN Mechatronics & Robotics“ arbeiten, welche ein günstiges mobiles EKG – also ein Messgerät für das Elektrokardiogramm, bzw. die Herzspannungskurve – für Sportler und Bedürftige aufbauen möchte. Das Messsignal hat dabei nur wenige Millivolt und Mikroampere. Um das Signal auf dem Weg von der aufgeklebten Elektrode zur Auswerteelektronik vor elektromagnetischer Einstrahlung zu schützen, ist eine Abschirmung um die Leitung gelegt (siehe Abb. 1). Da dadurch aber ein parasitärer Kondensator aufgebaut wird, hat Ihnen ein Kollege eine aktive Schirmung vorgeschlagen. Dabei wird die Abschirmung über einen Spannungsfolger immer auf der Messspannung gehalten, welche an der Leitung anliegt (siehe Abb. 2). Der parasitäre Kondensator wird durch diesen Aufbau nie geladen, da auf seinen beiden Seiten die gleiche Spannung herrscht - es entsteht keine Verfälschung des Signals. Wichtig ist für die Anwendung, dass der Spannungsfolger schnell reagiert.
Sie sind mit der Auslegung dieses Spannungsfolgers betreut und sollen die verfügbaren Operationsverstärker $LM318$, $uA741$ und $uA776$ in der Spannungsfolger-Schaltung (vgl. Skript Seite) analysieren.
Es ist ein kurzer Bericht (Problembeschreibung, Schaltung aus Tina, Ergebnisse, Diskussion) zu erstellen; als Analysewerkzeug ist Tina TI zu verwenden.
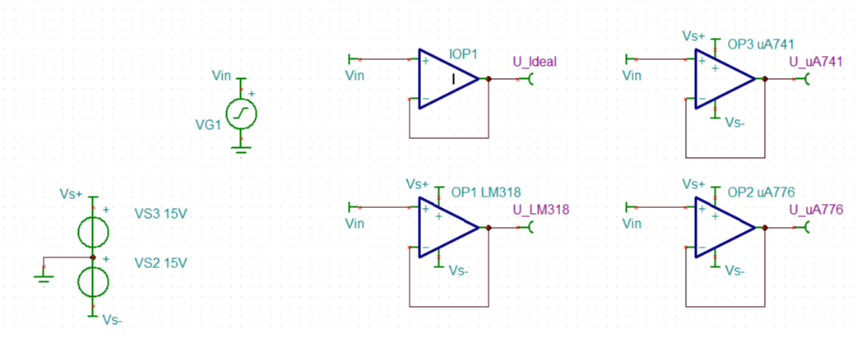
- Bilden Sie die oben beschriebene Schaltung für einen realistischen Operationsverstärker in Tina nach. Nutzen Sie dabei als Quelle einen Spannungsgenerator als Sprungfunktion („Unit step“) mit der Amplitude $U_A = 1,0 V$ .
- Simulieren Sie über „Analysis“»“Transient…“ für die angegebenen Operationsverstärker den Zeitverlauf.
Bestimmen Sie jeweils die Zeit die verstreicht bis der Ausgangswert von $0,1 V$ zum ersten mal $0,9 V$ erreicht (10% bis 90% der Amplitude, auch Anstiegszeit genannt). - Beschreiben Sie jeweils den Zeitverlauf. Gibt es neben der Anstiegszeit weitere Unterschiede?
- Welchen der drei Operationsverstärker würden Sie – auf Basis der angegebenen Informationen – für das Problem wählen?
Vertiefende Informationen (nicht relevant für Hausarbeit):
- Masterarbeit zu Entwicklung und Bau eines Demonstrationsmessgeräts
- Detaillierte Beschreibung einer EMG/EKG Vorverstärkerschaltung
1. Nachbildung der Schaltung
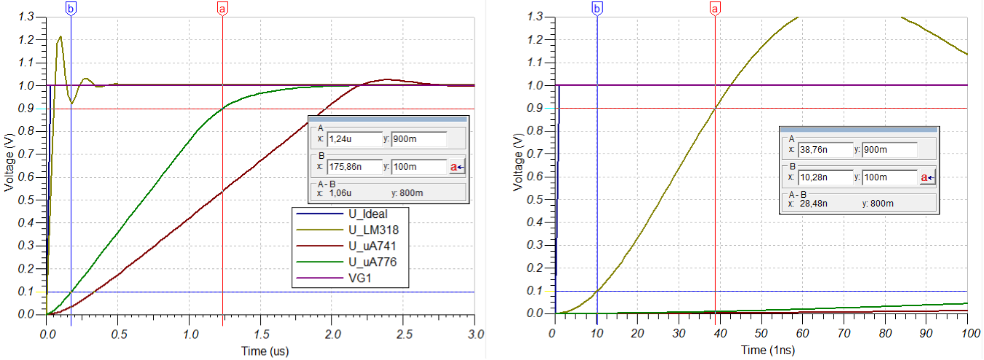
2. Zeitverlauf und Anstiegszeit
Anstiegszeit
- $LM318$: $28,5ns$
- $uA741$: $1,62\mu s$
- $uA776$: $1,05\mu s$
3. Beschreibung des Zeitverlaufs und Unterschiede
- $LM318$: schwingt zwar stark über (um >30%), aber trotzdem schneller ein als alle anderen.
- $uA741$: schwingt ohne Überschwingen ein, aber benötigt länger als der $LM318$
- $uA776$: ist der langsamste OPV und schwingt zudem über.
4. Geeigneter OPV
Unter der Vorgabe, dass der schnellste Spannungsfolger mit der kürzesten Anstiegszeit gesucht wird, ist der $LM318$ der beste OPV.
Aufgabe 3.5.1 invertierender Verstärker
Aufgabe 3.5.1 invertierender Verstärker
Leiten Sie für den invertierenden Verstärker die Spannungsverstärkung her. Nutzen Sie dabei das Vorgehen, welches für den nicht-invertierenden Verstärker verwendet wurde.
Berücksichtigen Sie, dass für die Differenzverstärkung $A_D$ des idealen OPV gilt: $A_D \rightarrow \infty$.
Damit ist gilt auch: $1/A_D \rightarrow 0$ , aber es gilt nicht immer ${{C}\over{U_x \cdot A_D}} \rightarrow 0$, für eine unbekannte Kontante $C$ und eine Spannung $U_x$!
1. Was ist gesucht?
$A_V = \frac{U_A}{U_E}$
2. Anzahl der Variablen?
- 5 Spannungen: $U_E$, $U_1$, $U_D$, $U_2$, $U_A$
- 5 Ströme: $I_1$, $I_m$, $I_p$, $I_2$, $I_o$
- --> 10 Variablen
3. Anzahl der notwendigen Gleichungen?
- 9, da eine Gleichung gesucht ist
4. Aufstellen der bekannten Gleichungen
- Grundgleichung: (1) $U_A = A_D \cdot U_D$
- Goldene Regeln:
- $R_D \rightarrow \infty$, und damit (2) + (3) $I_m = I_p = 0$
- $R_A = 0$
- (4) $A_D \rightarrow \infty$ und mit (1) $U_D = \frac{U_A}{A_D} \rightarrow 0$
- Maschen
- Masche 1: (5) $-U_E + U_1 - U_D = 0$
- Masche 2: (6) $U_D + U_2 + U_A = 0$
- Knoten: (7) $I_1 - I_2 + 0 = 0$
- Widerstände:
- (8) $R_1 = \frac{U_1}{I_1}$
- (9) $R_2 = \frac{U_2}{I_2}$
5. Herleitung der Spannungsverstärkung
\begin{align*} A_V &= \frac{U_A}{U_E} \quad | \quad mit (5) und (6) \\ A_V &= \frac{- U_D - U_2}{U_1 - U_D} \quad | \quad mit (8) und (9) \\ A_V &= \frac{- U_D - R_2 \cdot I_2}{R_1 \cdot I_1 - U_D} \quad | mit (1) \\ A_V &= \frac{- R_2 \cdot I_2}{R_1 \cdot I_1} \quad | mit (7) \\ A_V &= -\frac{R_2 }{R_1 } \end{align*}
6. Welcher der Verstärker (invertierender oder nicht invertierender) hat einen geringeren Eingangswiderstand? Warum?
Der Eingangswiderstand vom invertierenden Verstärker ist $R_1$.
Der vom nicht-invertienden ber größer als der Eingangswiderstand des OPV.
Damit hat der invertierenden Verstärker den geringeren Eingangswiderstand.
Aufgabe 3.5.2. Variationen des nicht-invertierenden Verstärkers
Aufgabe 3.5.2. Variationen des nicht-invertierenden Verstärkers
Auf den folgenden Seiten finden Sie Schaltungen mit einem idealen Operationsverstärker, welche dem nicht-invertierenden Verstärker ähneln und deren Spannungsverstärkung $A_V$ zu ermitteln ist.
Annahmen
- $R_1 = R_3 = R_4 = R$
- $R_2 = 2 \cdot R$
- $U_E$ entstammt einer niederohmigen Quelle
- $U_A$ liegt an einem hochohmigen Verbraucher an
Aufgaben
- Geben Sie für jede Schaltung die Spannungsverstärkung $A_V$ an. Eine detaillierte Rechnung wie bisher ist nicht notwendig.
- Geben Sie für die Abbildung 8 an, wie die Spannungsverstärkung ermittelt werden kann.
- Verallgemeinern Sie mit Begründung wie
- ein Kurzschluss der beiden OPV Eingänge zu berücksichtigen ist,
- Widerstände zu berücksichtigen sind, wenn diese
- mit einer Klemme („auf einer Seite“) direkt und ausschließlich an einem OPV Eingang liegen,
- mit je einer Klemme direkt an einem OPV Eingang liegen.
- In welchen Schaltungen stellen die Widerstände $R_3$ und $R_4$ einen unbelasteten Spannungsteiler dar?
Um sich den Problemen zu nähern, sollten Sie versuchen die Kenntnisse aus dem invertierenden Verstärker nutzen. Es kann sich anbieten die Schaltungen über Falstad-Circuit oder Tina TI zu simulieren. Als Unterstützung sind in den ersten beiden Schaltungen Tipps unter der Abbildung zu sehen.
Wichtig: Wie immer im Studium sollten Sie versuchen die Kenntnisse aus der Aufgabe zu verallgemeinern.
Tipps
- Wie groß ist der Stromfluss in den invertierenden und nicht invertierenden Eingang bei einem idealen Operationsverstärker? Welchen Spannungsabfall würde es also an einem Widerstand geben, dessen einer Anschluss nur zu einem Eingang des Operationsverstärkers führt?
- Der Operationsverstärker versucht stets soviel Strom am Ausgang auszugeben, damit sich zwischen invertierendem und nicht invertierendem Eingang die benötigte minimale Spannung $U_D$ ergibt. Wie groß kann $U_D$ angenommen werden? Kann diese Spannung auch über einen Widerstand aufgebaut werden?
- Können verschiedene Widerstände (z.b. weil diese zwischen den gleichen Knoten liegen) zusammengefasst werden?
Abb. 1
- Zwischen inv. und nicht-inv. Eingang liegt nur $U_D \rightarrow 0$ an. Solange $R_4 > 0$ ist, kann dort die kleine Spannung anliegen. $R_4$ kann also durch eine offene Leitung ersetzt werden.
- Da durch $R_3$ kein Strom fließt, ergibt sich keine Spannungsdifferenz über $R_3$. Damit kann $R_3$ durch einen Kurzschluss ersetzt werden.
- Es ergibt sich somit ein nicht-invertierender Verstärker mit $A_V = 3/2$
Abb. 2
- Durch $R_3$ fließt kein Strom, da kein Strom in den OPV einfließen kann. Damit ergibt sich keine Spannungsdifferenz über $R_3$. Damit kann $R_3$ durch einen Kurzschluss ersetzt werden.
- $R_4$ und $R_2$ liegen parallel und ergeben $R_g = \frac{2}{3} R_1$
- Die Verstärkung wird damit zu $A_V = \frac{R_g + R_1}{R_g} = 2,5$
Abb. 3
- $R_3$ und $R_4$ ergeben einen unbelasteten Spannungsteiler.
- Damit wird die Eingangspannung halbiert.
- Es ergibt sich somit ein nicht-invertierender Verstärker mit $A_V = \frac{R_2 + R_1}{R_2} = 0,75$
Abb. 4
- Durch $R_3$ fließt kein Strom, da kein Strom in den OPV einfließen kann. Damit ergibt sich keine Spannungsdifferenz über $R_3$. Damit kann $R_3$ durch einen Kurzschluss ersetzt werden.
- Da die Eingangsspannung aus einer niederohmigen Spannungsquelle kommt ist $R_4$ im Gegensatz zum Innenwiderstand der Spannungsquelle vernachlässigbar. Damit kann $R_4$ durch eine offene Leitung ersetzbar
- Die gesamte Verstärkung wird damit zu $A_V = 3/2 $
Abb. 5
- Durch $R_3$ fließt kein Strom, da kein Strom in den OPV einfließen kann. Damit ergibt sich keine Spannungsdifferenz über $R_3$. Damit kann $R_3$ durch einen Kurzschluss ersetzt werden.
- $R_4$ und $R_2$ liegen parallel und ergeben $R_g = \frac{2}{3} R_1$
- Die Verstärkung wird damit zu $A_V = \frac{R_g + R_1}{R_g} = 2,5$
Abb. 6
- Durch $R_4$ fließt kein Strom, da kein Strom in den OPV einfließen kann. Damit ergibt sich keine Spannungsdifferenz über $R_4$. Damit kann $R_4$ durch einen Kurzschluss ersetzt werden.
- Da der invertierende somit auf 0V liegt, ergibt die Ausgangsspannung die maximal mögliche Spannung des OPV.
Abb. 7
- Die Eingangsspannung liegt an $R_4$ an, damit fließt dadurch $I= U_E / R$. Dieser Strom fließt auch durch $R_3$. Über beide liegt also $2 \cdot U_E$
- Die Widerstände $R_2$, $R_3$ und $R_4$ ergeben einen $R_g = (R_3 + R_4)||R_2 = 2R||2R = R$
- Damit ist $R_g$ = $R_1$ und die Ausgangsspannung $U_A$ zweimal die Spannung über $R_g$ und somit ergibt aish $A_V = 4$
Abb. 8
- Der invertierende und der nicht invertierende Eingang sind kurzgeschlossen, also ist die Ausgangspannung gleich 0
Abb. 9
- Zwischen inv. und nicht-inv. Eingang liegt nur $U_D \rightarrow 0$ an. Solange $R_3 > 0$ ist, kann dort die kleine Spannung anliegen. $R_3$ kann also durch eine offene Leitung ersetzt werden.
- Da durch $R_4$ kein Strom fließt, ergibt sich keine Spannungsdifferenz über $R_4$. Damit kann $R_4$ durch einen Kurzschluss ersetzt werden.
- Es ergibt sich somit ein nicht-invertierender Verstärker mit $A_V = \frac{R_2 + R_1}{R_2} = 1,5$
Zu 1. Alle Lösungen:
| Aufg. 1 | Aufg. 2 | Aufg. 3 | Aufg. 4 | Aufg. 5 | Aufg. 6 | Aufg. 7 | Aufg. 8 | Aufg. 9 |
|---|---|---|---|---|---|---|---|---|
| $A_V = 1,5$ | $A_V = 2,5$ | $A_V = 0,75$ | $A_V = 1,5$ | $A_V = 2,5$ | $A_V \rightarrow \infty$ | $A_V = 4$ | $A_V = 0$ | $A_V = 1,5$ |
Zu 2.
- Die Eingangsspannung liegt an $R_4$ an, damit fließt dadurch $I= U_E / R$. Dieser Strom fließt auch durch $R_3$. Über beide liegt also $2 \cdot U_E$
- Die Widerstände $R_2$, $R_3$ und $R_4$ ergeben einen $R_g = (R_3 + R_4)||R_2 = 2R||2R = R$
- Damit ist $R_g$ = $R_1$ und die Ausgangsspannung $U_A$ zweimal die Spannung über $R_g$ und somit ergibt aish $A_V = 4$
Zu 3.
- Ein Kurzschluss von $U_p$ und $U_m$ führt zu $U_D=0$ und damit zu $U_A =0$
- Widerstände die mit einer Klemme („auf einer Seite“) direkt und ausschließlich an einem OPV Eingang liegen, können durch einen Kurzschluss ersetzt werden, da kein Strom durch sie fließt.
- Widerstände die mit je einer Klemme direkt an einem OPV Eingang liegen, können durch einen offene Leitung ersetzt werden, da die minimale Spannung in jedem Fall aufgebaut werden kann.
Zu 4.
Unbelastete Spannungsteiler von $R_3$ und $R_4$ sind in folgenden Schaltungen vorhanden: 3, 7, 8, ggf. auch 1 und 9.