6 Das stationäre elektrische Strömungsfeld

6.1 Stromstärke und Strömungsfeld

Stromstärke und Stromdichte im einfachen Fall

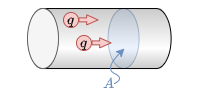
Die Stromstärke wurde bisher als „Ladung pro Zeit“ ($I={{{\rm d}Q}\over{{\rm d}t}}$) begriffen. Mikroskopisch betrachtet ist der elektrische Strom die gerichtete Bewegung von elektrischen Ladungsträgern. Im Kapitel Grundlagen und Grundbegriffe sind wir auf das Bild des durch eine Querschnittsfläche $A$ durchdringenden Ladungsträgerstromes bereits eingegangen (siehe Abbildung 1). Weiterhin hatten wir in der Gleichstromtechnik ganz praktisch das ohmsche Gesetz mit $R = {{U}\over{I}}$ angewandt. Nun wissen wir aber, dass aus dem elektrostatischen Feld das die Spannung sich aus der elektrischen Feldstärke herleiten lässt. Wie ist das aber nun beim Strom?

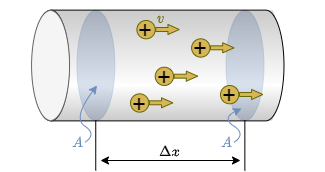
Dazu wird das Paket ${\rm d}Q$ an Ladungen betrachtet, welches zukünftig in dem Zeitraum ${\rm d}t$ die Fläche $A$ passieren wird. Diese Ladungen befinden sich in einem Teilvolumenelement ${\rm d}V$, welches durch die zu durchtretende Fläche $A$ und einem Teilabschnitt ${\rm d}x$ gegeben ist: ${\rm d}V = A \cdot {\rm d}x$. Die Menge an Ladungen pro Volumen wird durch die Ladungsträgerdichte angegeben, speziell bei Metallen durch die Elektronendichte $n_{\rm e}$. Die Elektronendichte $n_{\rm e}$ gibt die Anzahl der freien Elektronen je Volumeneinheit a. Diese liegt z.B. bei Kupfer etwa bei $n_{\rm e}(Cu)=8,47 \cdot 10^{19} ~\rm {{1}\over{mm^3}}$.

Die in dem Teilvolumenelement ${\rm d}V$ enthaltenen, strömenden Ladungen sind dann (mit der Elementarladung $e_0$):

\begin{align*} {\rm d}Q = n_{\rm e} \cdot e_0 \cdot A \cdot {\rm d}x \end{align*}

Die Stromstärke ist dann mit $I={{{\rm d}Q}\over{{\rm d}t}}$:

\begin{align*} {{{\rm d}Q} \over{{\rm d}t}} = n_{\rm e} \cdot e_0 \cdot A \cdot {{{\rm d}x}\over{{\rm d}t}} = n_{\rm e} \cdot e_0 \cdot A \cdot v_e \end{align*}

Es ergibt sich so eine Elektronengeschwindigkeit $v_{\rm e}$ von:

\begin{align*} v_{\rm e} = {{{\rm d}x}\over{{\rm d}t}} = {{I}\over{n_{\rm e} \cdot e_0 \cdot A }} \end{align*}

Die Ladungsträger sind also nun - im Gegensatz zu den Betrachtungen in der Elektrostatik mit endlichen Geschwindigkeiten unterwegs. Mit Blick auf die Elektronengeschwindigkeit $v_{\rm e} \sim {{I}\over{A}}$ liegt es nahe eine (auf die Fläche bezogene) Stromdichte $S$ zu bestimmen:

\begin{align*} \boxed{S = {{I}\over{A}}} \end{align*}

In einigen Büchern wird auch der Buchstabe $J$ für die Stromdichte genutzt.

Feldlinien und Äquipotentialflächen des elektrischen Strömungsfeldes

Wie auch beim elektrostatischen Feld soll auch hier eine homogene Feldform und die inhomogene Feldform gegenübergestellt werden:

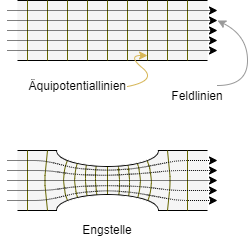
1. Homogenes Strömungsfeld
   z.B. Leiter mit konstantem Querschnitt
   1. Feldlinien des Stroms verlaufen parallel
   2. Äquipotentialflächen
      1. stehen dazu stets senkrecht, da die potentielle Energie einer Ladung nur von der Position entlang des Weges abhängt
      2. sind aufgrund des konstanten elektrischen Feldes, welches den Strom verursacht und der homogenen Geometrie äquidistant
   3. Strom $I = S \cdot A$ ist konstant
      $\rightarrow$ Ladungsträger haben die gleiche Geschwindigkeit $v$
2. Inhomogenes Strömungsfeld
   Schmelzsicherung oder Verjüngung im Draht
   1. Feldlinien des Stroms verlaufen nicht parallel
   2. Strom $I = S \cdot A$ muss auch konstant sein, da die Ladung nicht verschwindet / erzeugt wird, aber die Fläche $A$ wird geringer
      $\rightarrow$ damit muss die Stromdichte $S$ und die Geschwindigkeit $v$ an der Engstelle größer werden
   3. Äquipotentialflächen
      1. stehen auch dazu wieder senkrecht.
      2. zeigen nun eine Verdichtung bei der Engstelle

Warum ergibt sich aber eine Verdichtung der Äquipotentialflächen bei der Engstelle? Diese bedeutet anschaulich, dass dort eine große Potentialdifferenz, also eine große Spannung abfällt. Das klingt also schon etwas plausibel. Tiefer soll dies gleich nochmal betrachtet werden.

Die Stromdichte wurde nur für eine konstante Querschnittsfläche $A$ bestimmt, durch welche ein homogener Strom, also auch ein homogenes Strömungsfeld, rechtwinklig durchtritt. Nun soll aber ein allgemeiner Ansatz für die elektrische Stromstärke gefunden werden.

Hierzu wird zunächst statt einer konstanten Stromdichte $S$ über einer senkrechten, geraden Querschnittsfläche $A$, eine variierende Stromdichte $S(A)$ über viele kleine Teilflächen $dA$ betrachtet. Damit kann - wenn die Teilflächen hinreichend klein sind - wieder eine konstante Stromdichte über die Teilfläche erhalten werden. Es wird dann also aus

\begin{align*} I = S \cdot A \rightarrow {\rm d}I = S \cdot {\rm d}A \end{align*}

Der Gesamtstrom über eine größere Fläche $A$ ergibt sich somit als:

\begin{align*} I = \int {\rm d}I = \iint_A S \cdot {\rm d}A \end{align*}

Was hierbei aber nicht betrachtet wurde: Die gewählte Fläche $A$ muss nicht zwangsläufig senkrecht auf der Stromdichte $S$ stehen. Um dies zu berücksichtigen, kann der (Teil)Flächennormalenvektor ${\rm d}\vec{A}$ genutzt werden. Wenn nur der Teil der Stromdichte $\vec{S}$ betrachtet werden soll, welcher in Richtung von ${\rm d}\vec{A}$ wirkend, so lässt sich dies über das Skalarprodukt ermitteln:

\begin{align*} I = \int {\rm d}I = \iint_A \vec{S} \cdot {\rm d}\vec{A} \end{align*}

Dies stellt die integrale Schreibweise der elektrischen Stromstärke dar. Mit dieser lässt sich die Stromstärke in einem beliebigen Feld ermitteln.

Allgemeines Materialgesetz

Für eine „pragmatische“ Herleitung des allgemeinen Materialgesetzes zur Stromdichte soll nun nochmal auf die Verdichtung der Äquipotentialflächen bei der Engstelle eingegangen werden. Zwischen zwei Äquipotentialflächen ist eine Spannungsdifferenz $\Delta U$ vorhanden. Wählt man diese hinreichend klein ergibt sich wieder der Übergang von $\Delta U \rightarrow {\rm d}U$. Durch die Potentialflächen muss aber im Leiter stets der gleiche Strom $I$ fließen. Aus dem Ohm'schen Gesetz ergibt sich dann für den Teilwiderstand ${\rm d}R$ zwischen den zwei Äquipotentialflächen:

\begin{align*} {\rm d}U = I \cdot {\rm d}R \tag{6.1.1} \end{align*}

Die einzelnen Größen sollen nun für infinitesimal kleine Teilstücke betrachtet werden. Für $I$ wurde dazu schon eine Gleichung über eine Dichte - die Stromdichte - gefunden:

\begin{align*} I = S \cdot A \tag{6.1.2} \end{align*}

Aber auch $R$ wurde bereits schon durch eine „Dichte“ - dem spezifischen Widerstand $\varrho$ - ausgedrückt: $ R = \varrho \cdot {{l}\over{A}}$

Wenn ein Leiter aus dem gleichen Material betrachtet wird, ist der spezifische Widerstand $\varrho$ überall gleich. Ist aber nun entlang des Leiters ein Teilstück ${\rm d}s$ vorhanden, bei dem der Querschnitt $A$ kleiner ist, so ändert sich auch der Widerstand $dR$ dieses Teilelements. Der Teilwiderstand ist dann:

\begin{align*} {\rm d}R = \varrho \cdot {{{\rm d}s}\over{A}} \tag{6.1.3} \end{align*}

Konkret heißt dass also für die Engstelle: An der Engstelle steigt der Widerstand. Damit steigt dort auch der Spannungsabfall. Damit gibt es dort auch mehr Äquipotentialflächen.

Die Anreicherung der Äquipotentialflächen wäre damit gelöst. Interessanterweise lässt sich aber mit dem Gedankenmodell nun auch für einen homogenen Körper das allgemeine Materialgesetz erklären. Dazu fügt man Gleichung $(6.1.2)$ und $(6.1.3)$ in $(6.1.1)$ ein. Dann ergibt sich:

\begin{align*} {\rm d}U = I \cdot {\rm d}R = S \cdot A \cdot \varrho \cdot {{{\rm d}s}\over{{A}}} = \varrho \cdot S \cdot {\rm d}s \\ \end{align*}

Wird nun die elektrische Feldstärke als $E={{{\rm d}U}\over{{\rm d}s}}$ eingefügt, erhält man:

\begin{align*} E = {{{\rm d}U}\over{{\rm d}s}} = \varrho \cdot S \end{align*}

Mit einer ausführlicheren (und mathematisch korrekten) Herleitung erhält man:

\begin{align*} \boxed{\vec{E} = \varrho \cdot \vec{S} } \end{align*}

Diese Gleichung drückt aus, wie das elektrische Feld $\vec{E}$ und das (stationäre) elektrische Strömungsfeld $\vec{S}$ zusammenhängen: beide zeigen in die gleiche Richtung. Bei einem vorgegebenen, elektrischen Feld $\vec{E}$ in einem homogenen Leiter wird das Strömungsfeld $\vec{S}$ um so größer, je kleiner der spezifische Widerstand $\varrho$ ist.

Aufgabe

6.2 Gaußscher Satz des Strömungsfeldes

Video

Warum fließt ein Elektronen durch einen Kondensator

Aufgaben