Inhaltsverzeichnis
4 Netzwerke bei veränderlicher Frequenz
Weiterführende Inhalte sind beim elektroniktutor zu finden
Einführung
In den vorherigen Kapitel wurde erklärt, wie die „Beeinflussung eines sinusförmigen Stromflusses“ von Kondensator und Induktivitäten aussehen. Um dies zu beschrieben wurde die Impedanz eingeführt. Diese kann bei sinusförmiger Anregung als komplexwertiger Widerstand verstanden werden.
Es gilt für den Kondensator:
\begin{align*} \underline{U}_C = \frac{1}{j\omega \cdot C} \cdot \underline{I}_C \quad \rightarrow \quad \underline{Z}_C = \frac{1}{j\omega \cdot C} \end{align*}
und für die Induktivität
\begin{align*} \underline{U}_L = j\omega \cdot L \cdot \underline{I}_L \quad \rightarrow \quad \underline{Z}_L = j\omega \cdot L \end{align*}
Mit komplexen Impedanzen kann ganz ähnlich umgegangen werden wie mit den ohmschen Widerständen in Elektrotechnik 1 (siehe: einfache_gleichstromkreise, lineare_quellen_und_zweipole, analyse_von_gleichstromnetzen). Bei diesen Umformungen bleibt der Anteil $ j\omega \cdot$ erhalten. Schaltungen mit Impedanzen wie Induktivitäten und Kapazitäten werden entsprechend eine Frequenzabhängigkeit zeigen.
4.1 Frequenzabhängiger Spannungsteiler
Ziele
Nach dieser Lektion sollten Sie:
- wissen, dass ..
- wissen, dass sich … bildet.
- die … können.
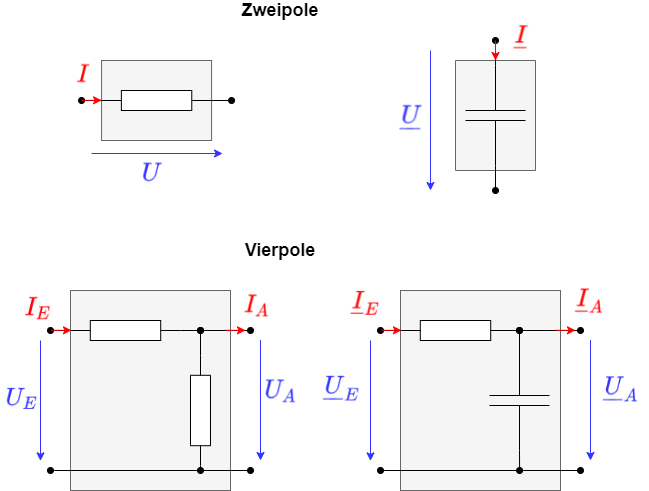
Vom Zweipol zum Vierpol
Bisher wurden Komponenten wie Widerstände, Kondensatoren und Induktivitäten als Zweipol verstanden. Dies liegt auch nahe, da es nur zwei Anschlüsse gibt. Im folgenden werden aber Schaltungen betrachtet, die sich ähnlich eines Spannungsteilers verhalten: Auf einer Seite liegt eine Spannung $U_E$ an, auf der anderen Seite bildet sich damit $U_A$. Es ergeben sich so 4 Klemmen. Die Schaltung kann und wird im folgenden als Vierpol betrachtet werden. Die Ein uns Ausgangsgrößen werden aber komplexwertig sein.
Bei den Vierpolen ist die Relation von „was geht raus“ (z.B. $\underline{U}_A$ oder $\underline{U}_2$) zu „was geht rein“ (z.B. Spannung $\underline{U}_E$ oder $\underline{U}_1$) wichtig. Damit ergibt sich aus den Aus- und Eingangsgrößen ($\underline{U}_A$) und ($\underline{U}_E$) der Quotient:
\begin{align*} \underline{A} & = \frac {\underline{U}_A}{\underline{U}_E} \\ & \text{mit} \; \underline{U}_E = U_E \cdot e^{j \varphi_{uE}} \\ & \text{und} \; \underline{U}_A = U_A \cdot e^{j \varphi_{uA}} \\ \\ \underline{A}& = \frac {\underline{U}_A}{\underline{U}_E} = \frac {U_A \cdot e^{j \varphi_{uA}}}{U_E \cdot e^{j \varphi_{uE}}} \\ & = \frac {U_A}{U_E}\cdot \cdot e^{j (\varphi_{uA}-\varphi_{uE})} \\ \end{align*} \begin{align*} \boxed{\underline{A} = \dfrac {\underline{U}_A}{\underline{U}_E} = \frac {U_A}{U_E}\cdot e^{j \Delta\varphi_{u}}} \end{align*}
Merke:
- Der komplexwertige Quotient ${\underline{U}_A}/{\underline{U}_E}$ wird Übertragungsfunktion genannt
- Der frequenzabhängige Betrag des Quotienten $A(\omega)={{U}_A)}/{{U}_E}$ wird Amplitudengang und die Winkeldifferenz $\Delta\varphi_{u}(\omega)$ Phasengang genannt.
Das Frequenzverhalten des Amplitudengangs und des Frequenzgangs ist nicht nur in Elektrotechnik und Elektronik wichtig, sondern wird auch in Regelungstechnik noch eine zentrale Rolle spielen.
RL-Reihenschaltung
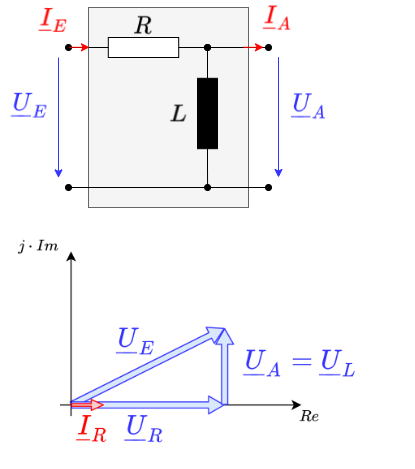
Es soll zunächst eine Reihenschaltung eines Widerstands $R$ und einer Induktivität $L$ betrachtet werden (siehe Abbildung 2). Diese Struktur wird auch RL-Glied genannt.
Hierbei ergibt sich für $\underline{U}_E= \underline{X_E} \cdot \underline{I}_E$ mit $\underline{X}_E = R + j\omega \cdot L$ und entsprechendes für $\underline{U}_A$:
\begin{align*}
\underline{A} = \dfrac {\underline{U}_A}{\underline{U}_E} = \frac {\omega L}{\sqrt{R^2 + (\omega L)^2}}\cdot e^{j\left(\frac{\pi}{2} - arctan \frac{\omega L}{R} \right)}
\end{align*}
Daraus ergibt sich für
- den Amplitudengang: $A = \frac {\omega L}{\sqrt{R^2 + (\omega L)^2}}$ und
- dem Phasengang: $\Delta\varphi_{u} = \frac{\pi}{2} - arctan \frac{\omega L}{R}$
Das Hauptaugenmerk soll zunächst auf dem Amplitudengang liegen. Dessen Frequenzverhalten lässt sich auf verschiedene Arten aus der Gleichung ableiten.
- Grenzwertbetrachtung der RL-Anordnung (in der Gleichung und im System)
- Plotten von Amplituden- und Frequenzgang
- Ermitteln von markanten Frequenzen
Diese drei Punkte sollen nun durchgegangen werden.
Grenzwertbetrachtung der RL-Anordnung
Zur Grenzwertbetrachtung wird betrachtet was, passiert, wenn die Frequenz $\omega$ an die Definitionsbereichsgrenzen läuft, also $\omega \rightarrow 0$ und $\omega \rightarrow \infty$:
- Für $\omega \rightarrow 0$ wird $A = \frac {\omega L}{\sqrt{R^2 + (\omega L)^2}} \rightarrow 0$, da der Zähler gegen null geht und der Nenner größer als Null bleibt.
- Für $\omega \rightarrow \infty$ läuft $A \rightarrow 1$, denn in der Wurzel im Nenner wird $(\omega L)^2$ im Verhältnis $R^2$ zu immer größer. Die Wurzel strebt also gegen $\omega L$ und damit gegen den Zähler.
Es ist also zu sehen, dass:
- bei kleinen Frequenzen keine Spannung $U_2$ am Ausgang anliegt
- bei großen Frequenzen $A = \frac {U_A}{U_E} = \rightarrow 1$ wird, also die Spannung am Ausgang der Spannung am Eingang gleicht.
Das dargestellte RL-Glied lässt also nur große Frequenzen passieren (= durchlaufen) und kleine werden weggefiltert. Die Schaltung entspricht einem Hochpass.
Dies lässt sich auch aus dem Verständnis der Bauteile herleiten: Bei kleinen Frequenzen ändert sich der Strom in der Spule und damit das Magnetfeld nur langsam. Es wird also nur eine vernachlässigbar kleine Gegenspannung induziert. Die Spule wirkt niederfrequent wie ein Kurzschluss. Bei höher werdenden Frequenzen ändert sich der durch $U_E$ erzeugte Strom durch die Spule schneller, die induzierte Spannung $U_i = - dI / dt$ wird groß. Die Spule hemmt dadurch den Stromfluss und es fällt eine Spannung an der Spule ab. Wird die Frequenz sehr hoch, so fließt nur ein vernachlässigbarer Strom durch die Spule - und damit auch durch den Widerstand. Der Spannungsabfall an $R$ geht damit gegen null und die Ausgangsspannung $U_A$ strebt gegen $U_E$.
Für die weitere Betrachtung soll die Gleichung der Übertragungsfunktion $\underline{A} = \dfrac {\underline{U}_A}{\underline{U}_E}$ so umgeschrieben werden, dass sie unabhängig von Bauteilwerten wird. Damit wird eine verallgemeinerte Darstellung möglich. Diese Darstellung wird als Normierung bezeichnet:
\begin{align*} \underline{A} = \dfrac {\underline{U}_A}{\underline{U}_E} = \frac {\omega L}{\sqrt{R^2 + (\omega L)^2}}\cdot e^{j\left(\frac{\pi}{2} - arctan \frac{\omega L}{R} \right)} \quad \quad \xrightarrow{\text{Normierung}} \quad \quad \underline{A}_{norm} = \frac {\omega L / R}{\sqrt{1 + (\omega L / R)^2}}\cdot e^{j\left(\frac{\pi}{2} - arctan \frac{\omega L}{R} \right)} = \frac {x}{\sqrt{1 + x^2}} \cdot e^{j\left(\frac{\pi}{2} - arctan x \right)} \end{align*}
Diese Gleichung verhält sich ganz gleich zu dem bisher betrachteten.
Plotten von Amplituden- und Frequenzgang
Die Übertragungsfunktion lässt sich auch zerlegt in Amplitudengang und Frequenzgang darstellen. Dazu bietet es sich an
- den Amplitudengang doppeltlogarithmisch und
- den Phasengang einfach logarithmisch
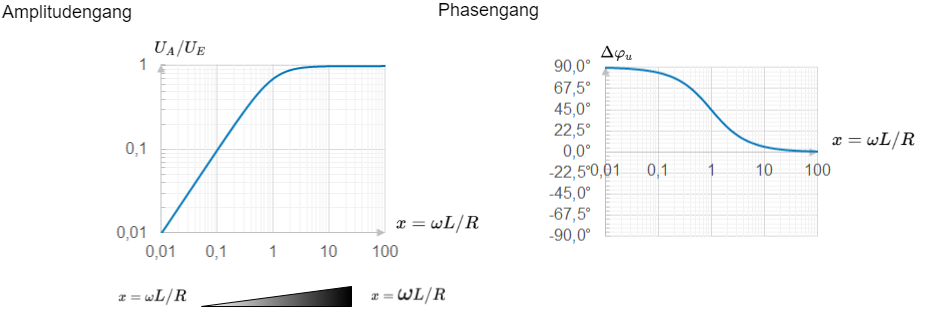
aufzuzeichnen. Abbildung 3 zeigt die beiden Diagramme. Auf der x-Achse wurde mit $x = \omega L / R$ die Normierungsvariable aufgetragen. Diese stellt eine gewichtete Frequenz dar.
Auch hier ist das bei der Grenzwertbetrachtung festgestellte Verhalten zu sehen: bei kleine Frequenzen $\omega$ (entspricht kleinen $x$) strebt der Amplitudengang gegen Null. Bei großen Frequenzen stellt sich ein Verhältnis $U_A / U_E = 1 $ ein.
Interessant ist im Phasengang der Punkt $x = 1$.
- Weiter links von diesem Punkt (also bei kleineren Frequenzen) erzeugt eine Verzehnfachung der Frequenz $\omega$ eine Verzehnfachung von $U_A / U_E$.
- Weiter rechts von diesem Punkt (also bei größeren Frequenzen) bleibt $U_A / U_E = 1$.
Dieser Punkt markiert also eine Grenze. Weit links davon ist der ohmsche Widerstand deutlich größer der Betrag der Impedanz der Spule: $R >> \omega L$.
weit rechts ist gerade umgekehrt.
Der Punkt $x=1$ kennzeichnet gerade die Grenzfrequenz. Es gilt
\begin{align*} \underline{A}_{norm} = \frac {x}{\sqrt{1 + x^2}} \cdot e^{j\left(\frac{\pi}{2} - arctan x \right)} = \frac {U_A}{U_E} \cdot e^{j\varphi}\quad \quad \left\{ \begin{array}{l} x \ll 1 & \widehat{=} \omega L \ll R &: \quad\quad \frac{U_A}{U_E}=x &, \varphi = \frac{\pi}{2} & \widehat{=} 90°\\ x \gg 1 & \widehat{=} \omega L \gg R &: \quad\quad \frac{U_A}{U_E}=1 &, \varphi = 0 & \widehat{=} 0°\\ x = 1 & \widehat{=} \omega L = R &: \quad\quad \frac{U_A}{U_E}=\frac{1}{\sqrt{2}} &, \varphi = \frac{\pi}{4} & \widehat{=} 45° \end{array} \right. \end{align*}
Merke:
- Die Grenzfrequenz beim Hoch- und Tiefpass ist die Frequenz, bei der der ohmsche Widerstand gerade dem Betrag der Impedanz gleicht.
- Die Grenzfrequenz trennt einen Bereich in dem der Filter Signale durchlässt von einem in dem diese unterdrückt (=gesperrt) werden.
- Bei der Grenzfrequenz wird die Phase $\varphi = 45°$ und die Amplitude $A = \frac{1}{\sqrt{2}}$.
Diese Aussagen gelten für einstufige, passive Filter, d.h. einem RL- oder einem RC-Glied. Mehrstufige Filter werden in der Schaltungstechnik betrachtet.
Die Grenzfrequenz in diesem Fall ergibt sich zu:
\begin{align*} R &= \omega L \\ \omega_{Gr} &= \frac{R}{L} \\ 2 \pi f_{Gr} &= \frac{R}{L} \quad \rightarrow \quad \boxed{f_{Gr} = \frac{R}{2 \pi \cdot L}} \end{align*}
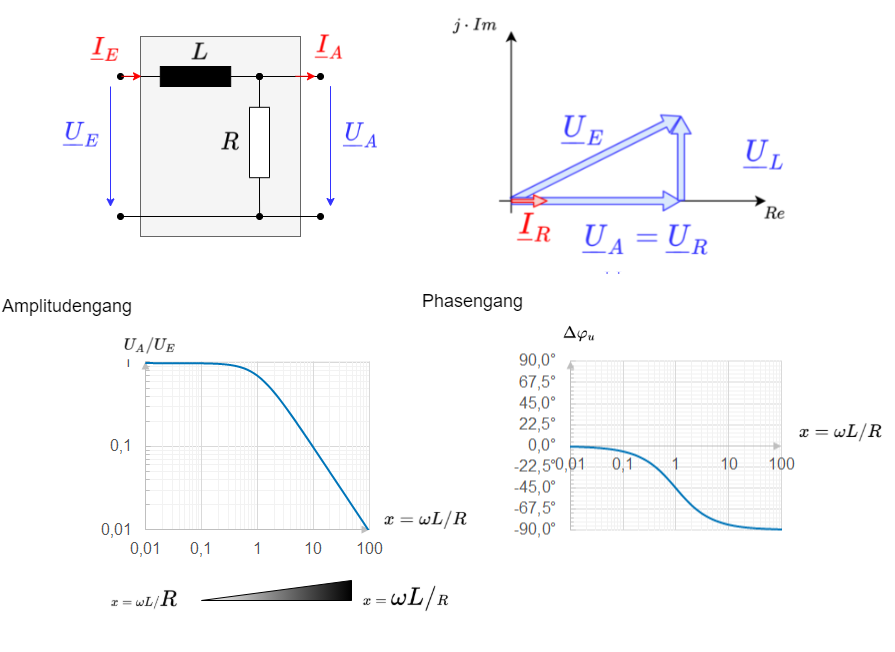
RL-Tiefpass
Bisher wurde nur eine Variante des RL-Glieds betrachtet, nämlich jenes, bei welchem die Ausgangsspannung $\underline{U}_A$ an der Induktivität abgegriffen wird. Hier soll kurz darauf eingegangen werden, was passiert, wenn die beiden Komponenten vertauscht werden.
In diesem Falle ergibt sich als normierte Übertragungsfunktion:
\begin{align*} \underline{A}_{norm} = \frac {1}{\sqrt{1 + (\omega L / R)^2}}\cdot e^{-j arctan \frac{\omega L}{R} } \end{align*}
Die Grenzfrequenz ist wieder über $f_{Gr} = \frac{R}{2 \pi \cdot L}$ gegeben.
RC-Reihenschaltung
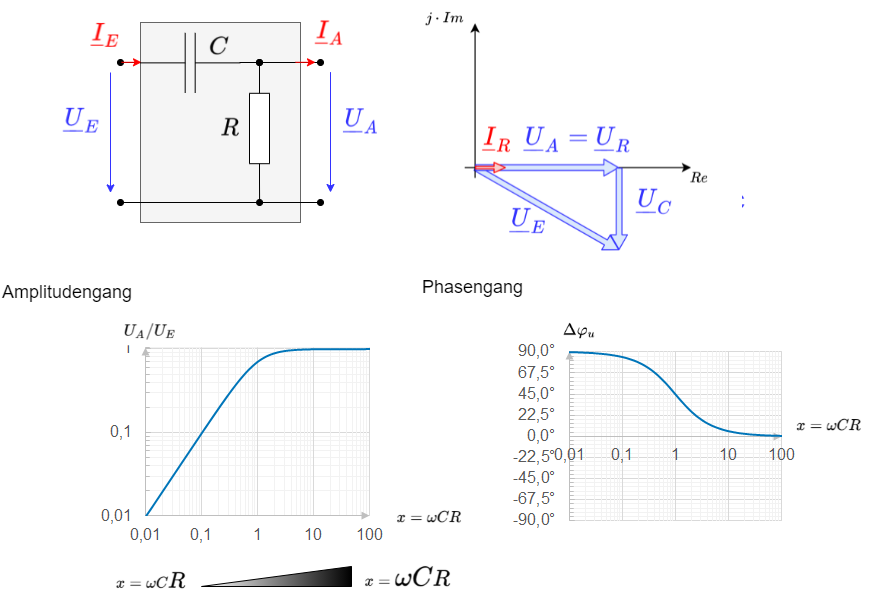
RC-Hochpass
Nun soll ein Spannungsteiler durch einen Widerstand $R$ und eine Kapazität $C$ aufgebaut werden. Ganz ähnlich zu den bisherigen Kapiteln kann hier auch die Übertragungsfunktion ermittelt werden.
Hier ergibt sich als normierte Übertragungsfunktion:
\begin{align*} \underline{A}_{norm} = \frac {\omega RC}{\sqrt{1 + (\omega RC)^2}}\cdot e^{\frac{\pi}{2}-j arctan \omega RC } \end{align*}
In diesem Fall wird die Normierungsvariable $x = \omega RC$. Auch hier wird die Grenzfrequenz über das Gleichsetzen von $R$ und dem Betrag der Impedanz der Kapazität ermittelt:
\begin{align*} R &= \frac{1}{\omega_{Gr} C} \\ \omega_{Gr} &= \frac{1}{RC} \\ 2 \pi f_{Gr} &= \frac{1}{RC} \quad \rightarrow \quad \boxed{f_{Gr} =\frac{1}{2 \pi\cdot RC} } \end{align*}
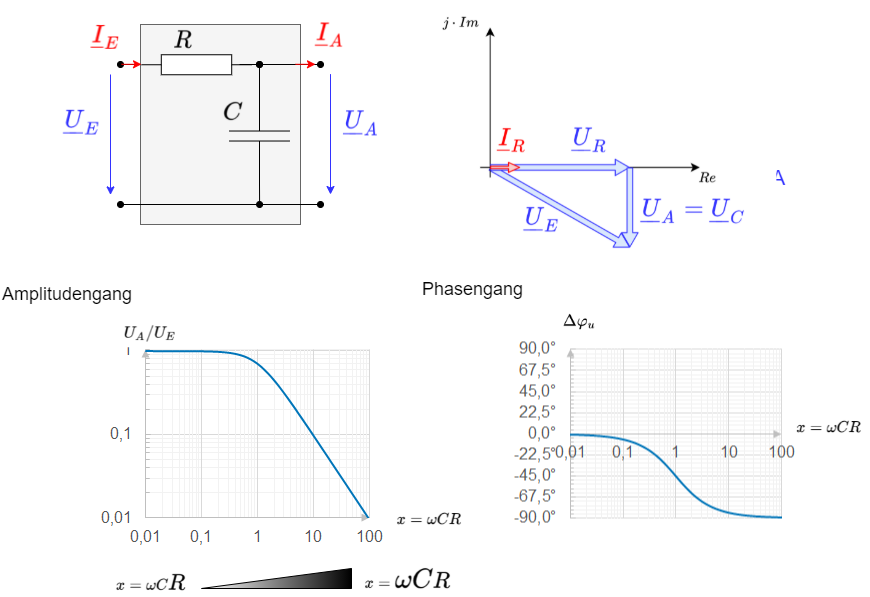
RC-Tiefpass
Auch hier soll die Spannung an der Impedanz als Ausgangsspannung genutzt werden. Damit ergibt sich ein Tiefpass.
Hier ergibt sich als normierte Übertragungsfunktion:
\begin{align*} \underline{A}_{norm} = \frac {1}{\sqrt{1 + (\omega RC)^2}}\cdot e^{-j arctan \omega RC } \end{align*}
Auch ist die Grenzfrequenz gegeben durch $f_{Gr} =\frac{1}{2 \pi\cdot RC}$
4.2 Resonanzerscheinungen
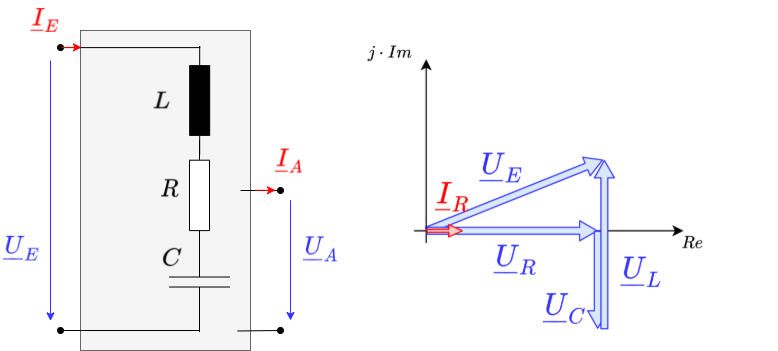
RLC - Serienschwingkreis
Wird ein Widerstand $R$ ein Kondensator $C$ und eine Induktivität $L$ in Reihe geschaltet, so ergibt sich ein Serienschwingkreis. Bei diesem ist die Ausgangsspannung nicht eindeutig definiert. Es muss im Folgenden betrachtet werden, wie sich die Spannungen über die einzelnen Komponenten verhalten. Die Gesamtspannung (= Eingangsspannung $U_E$) ergibt sich dabei zu:
\begin{align*} \underline{U} = \underline{U}_R + \underline{U}_L + \underline{U}_C \end{align*}
Da der Strom im Stromkreis konstant sein muss, kann hier die Gesamtimpedanz auf einfache Weise ermittelt werden:
\begin{align*} \underline{U} &= R \cdot \underline{I} + j \omega L \cdot \underline{I} + \frac {1}{j\omega C } \cdot \underline{I} \\ \underline{U} &= \left( R + j \omega L - j \cdot \frac {1}{\omega C } \right) \cdot \underline{I} \\ \underline{Z}_{ges} &= R + j \omega L - j \cdot \frac {1}{\omega C } \end{align*}
Als Betrag der (Eingangs)Spannung $U$ bzw. der (Eingangs- bzw. Gesamt)Impedanz $Z$ und die Phase ergeben sich zu:
\begin{align*} U &= \sqrt{U_R^2 + (U_Z)^2} = \sqrt{U_R^2 + (U_L - U_C)^2} \\ \end{align*}
\begin{align*} Z &= \sqrt{R^2 + (Z)^2} = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2} \\ \end{align*}
\begin{align*} \varphi_u = \varphi_Z &= arctan \frac{\omega L - \frac{1}{\omega C}}{R} \end{align*}
Es sind nun 3 unterschiedliche Situationen zu unterscheiden:
- Ist $U_L > U_C$ so verhält sich der gesamte Aufbau wie eine ohmsch-induktive Last. Dies ist bei hohen Frequenzen der Fall.
- Wird hier $U_L$ gleich $U_C$, so liegt die gesamte Eingangsspannung $U$ am Widerstand an. In diesem Fall ist der Gesamtwiderstand $Z$ minimal und nur ohmsch. \\Der Strom $I$ ist dann also maximal. Wenn der Strom maximal ist, so sind auch die Reaktionen der Kapazität und Induktivität - also deren Spannungen - maximal. Diese Situation ist der Resonanzfall.
- Ist $U_L < U_C$ so verhält sich der gesamte Aufbau wie eine ohmsch-kapazitive Last. Dies bei niedrigen Frequenzen ist der Fall.
Auch hier scheint es eine ausgezeichnete Frequenz zu geben, nämlich, wenn $U_L = U_C$ bzw. $Z_C = Z_L$ gilt:
\begin{align*} \frac{1}{\omega_0 C} & = \omega L \\ \omega_0 & = \frac{1}{\sqrt{LC}} \\ 2\pi f_0 & = \frac{1}{\sqrt{LC}} \rightarrow \boxed{ f_0 = \frac{1}{2\pi \sqrt{LC}} } \end{align*}
Die Frequenz $f_0$ wird Resonanzfrequenz genannt.
| $\quad$ | $f \rightarrow 0$ | $\quad$ | $f = f_0$ | $\quad$ | $f \rightarrow \infty$ | |
|---|---|---|---|---|---|---|
| Spannung $U_R$ am Widerstand | $\boldsymbol{0}$ | $\boldsymbol{U}$ da sich die Impedanzen gerade aufheben | $ \boldsymbol{0}$ | |||
| Spannung $U_L$ an der Induktivität | $\boldsymbol{0}$ da $\omega L$ sehr klein wird | $\boldsymbol{\omega_0 L \cdot I = \omega_0 L \cdot \frac{U}{R} = \color{blue}{\frac{1}{R}\sqrt{\frac{L}{C}}}\cdot U}$ | $\boldsymbol{U}$ da $\omega L$ sehr groß wird |
|||
| Spannung $U_C$ am Kondensator | $\boldsymbol{U}$ da $\frac{1}{\omega C}$ sehr groß wird | $\boldsymbol{\frac{1}{\omega_0 C} \cdot I = \frac{1}{\omega_0 C} \cdot \frac{U}{R} = \color{blue}{\frac{1}{R}\sqrt{\frac{L}{C}}}\cdot U}$ | $\boldsymbol{0}$ da $\frac{1}{\omega C}$ sehr klein wird |
Die Rechnung in der Tabelle zeigt, dass im Resonanzfall die Spannung am Kondensator bzw. an der Induktivität um den Faktor $\color{blue}{\frac{1}{R}\sqrt{\frac{L}{C}}}$ von der Eingangsspannung abweichen. Diese Größe wird Güte $Q_S$ genannt:
\begin{align*} \boxed{ Q_S = \frac{U_C}{U} |_{\omega = \omega_0} = \frac{U_L}{U} |_{\omega = \omega_0} = \color{blue}{\frac{1}{R}\sqrt{\frac{L}{C}}} } \end{align*}
Die Güte kann größer, kleiner oder gleich 1 sein.
- Ist die Güte sehr groß, so wird im Resonanzfall die Überschwingung der Spannungen an den Impedanzen sehr groß. Dies ist bei verschiedenen Anwendungen nützlich und notwendig z.B. bei einem RLC-Glied als Antenne.
- Ist die Güte sehr klein, so ist kein Überschwingen mehr zu sehen. Je nachdem an welcher Impedanz die Ausgangsspannung gemessen wird, bildet sich ein Hochpass oder Tiefpass aus ähnlich dem RC- bzw. dem RL-Glied. Dieser hat aber eine steilere Steigung im sperrenden Bereich. Das bedeutet, dass die Filterwirkung besser ist.
Der Kehrwert der Güte wird Dämpfung $d_S$ genannt. Dieser wird bei der Nutzung der Schaltung als einen nicht-überschwingenden Filter angegeben.
\begin{align*} \boxed{ d_S = \frac{1}{Q_S} = R \sqrt{\frac{C}{L}} } \end{align*}
Entkoppelkondensator am Mikrocontroller
Hinweis: Die Simulation gibt ein stark vereinfachtes Bild wieder. Die Reaktion des Mikrocontroller ist auf ein Dreiecksignal reduziert dargestellt, da die Flankensteilheit der Spannungen nicht abgebildet werden können. Eine reale Simulation erfordert ein leistungsfähiges SPICE-Programm, in welchem die Leitungstheorie abgebildet werden kann.
Weitere Details sind sind hier (Praxis) oder hier (Platinen-Layout) zu finden.