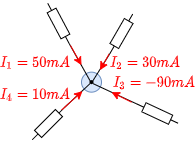Inhaltsverzeichnis
2 Einfache Gleichstromkreise
Bisher wurden nur einfache Stromkreise aus einer Quelle und einem mit Leitungen verbundenen Verbraucher betrachtet.
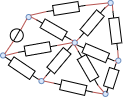
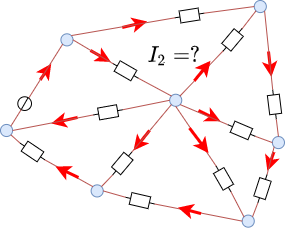
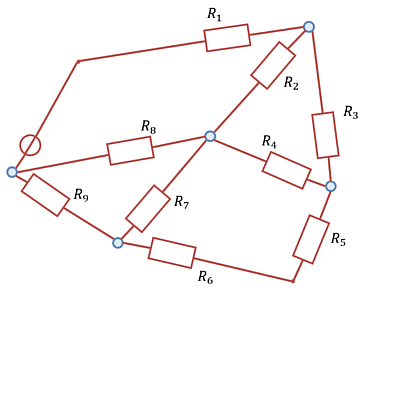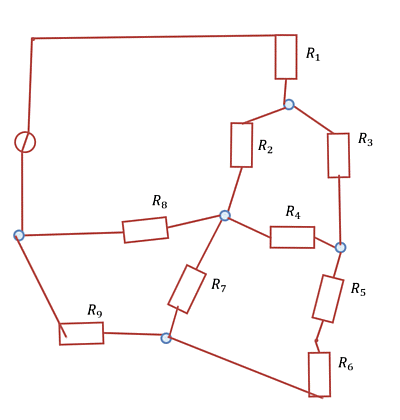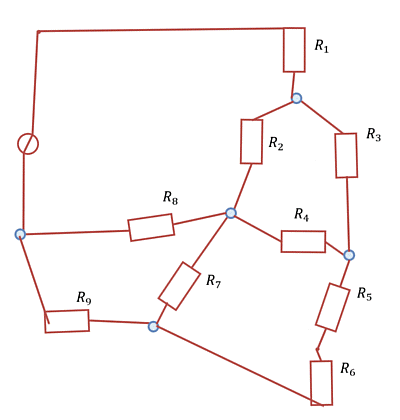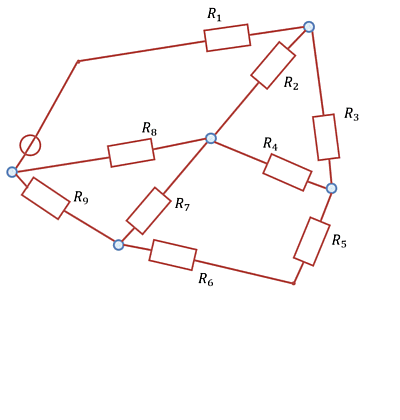
Im Folgenden werden kompliziertere Schaltungsanordnungen analysieren. Diese beinhalten zunächst nur eine Quelle, aber mehrere Leitungen und viele ohmsche Verbraucher (vgl. Abbildung 1).
2.1 ideale Bauelemente
Ziele
Nach dieser Lektion sollten Sie:
- die Darstellung von idealen Strom- und Spannungsquellen im U-I-Diagramm kennen.
- wissen, welchen Innenwiderstand ideale Strom- und Spannungsquellen haben.
- das Symbol von idealen Strom- und Spannungsquellen kennen.
- die Eigenschaften des idealen Widerstands und der idealen Verbindung kennen.
Jeder elektrische Stromkreis besteht aus drei Elementen:
- Verbraucher: Verbraucher wandeln die elektrische Energie in eine nicht rein-elektrische Energie um.
z.B.- in elektrostatische Energie (Kondensator)
- in magnetostatische Energie (Magnet)
- in elektromagnetische Energie (LED, Glühbirne)
- in mechanische Energie (Lautsprecher, Motor)
- in chemische Energie (Laden eines Akkumulators)
- Erzeuger (Quellen): Erzeuger wandeln die Energie aus einer anderen Energieform in elektrisch Energie. (z.B. Generator, Batterie, Photovolatik)
- Verbindungen (bzw. Stromnetz): die Verbindungsleitungen verknüpfen Verbraucher mit Quellen.
Diese Elemente sollen im Folgenden näher betrachtet werden.
Verbraucher
- Der umgangssprachlicher Begriff Verbraucher steht in der Elektrotechnik für einen elektrischen Verbraucher - also einem Bauteil, welches die elektrische Energie in eine andere Energieform wandelt.
- Ein Widerstand wird häufig auch als Verbraucher bezeichnet. Neben den reinem ohmschen Verbraucher existieren aber auch ohmsch-induktive Verbraucher (z.B. Spulen im Motor) oder ohmsch-kapazitive Verbraucher (z.B. verschiedene Netzteile durch Kondensatoren am Ausgang). Entsprechend ist die Gleichsetzung von Widerstand und Verbraucher falsch.
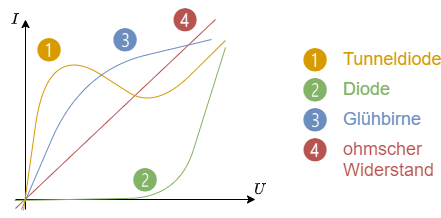
- Strom-Spannungs-Kennlinien (vgl. Abbildung 2)
- Strom-Spannungs-Kennlinien eines Verbrauchers verlaufen immer durch den Ursprung, da ohne Strom keine Spannung anliegt und umgekehrt.
- Ohm'sche Verbraucher besitzen eine lineare Strom-Spannungs-Kennlinie, welche durch einen einzigen Zahlenwert beschrieben werden kann.
Die Steigung in der $U$-$I$-Kennlinie ist die Leitfähigkeit: $I = G \cdot U = {{U}\over{R}}$
Quellen
- Quellen wirken als Erzeuger elektrischer Energie
- Es werden ideale und reale Quellen unterschieden.
Die realen Quellen werden im nachfolgenden Kapitel (Lineare Quellen und Zweipole) beschrieben.
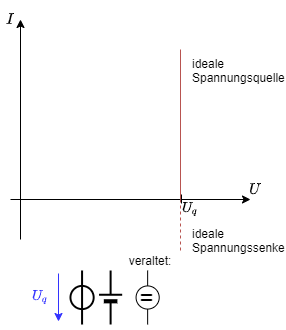
Die ideale Spannungsquelle erzeugt eine definierte Ausgangsspannung $U_q$.
Um diese Spannung zu halten kann sie einen beliebigem Strom abgeben.
Die Strom-Spannungs-Kennlinie stellt dies auch dar (siehe Abbildung 3).
Das Schaltzeichen zeigt einen Kreis mit zwei Anschlüssen. Im Kreis sind die beiden Anschlüsse kurzgeschlossen.
Eine weiteres Schaltzeichen zeigt den negativen Anschluss der Spannungsquelle als „dickes Minus“, der positive Anschluss ist breiter gezeichnet.
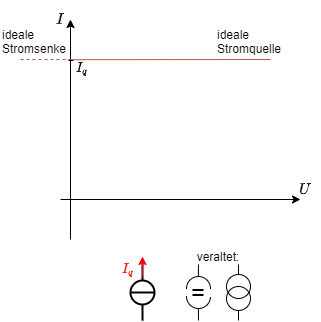
Die ideale Stromquelle erzeugt eine definierten Ausgangsstrom $I_q$.
Damit dieser Strom fließen kann, ist eine beliebigem Spannung an ihren Klemmen möglich.
Die Strom-Spannungs-Kennlinie stellt dies auch dar (siehe Abbildung 4).
Das Schaltzeichen zeigt einen Kreis mit zwei Anschlüssen. Im Kreis sind die beiden Anschlüsse offengelassen und eine Linie senkrecht dazu gezeichnet.
Verbindungen
- Die ideale Verbindungsleitung ist widerstandsfrei und übermittelt Strom und Spannung instantan.
- Real vorhandene Einflüsse (z.B. Spannungsabfall) von Verbindungen werden über separat gezeichnete Bauteile (z.B. ohmschen Widerstand) berücksichtigt.
2.2 Bezugspfeile und erste Betrachtung eines Gleichstromkreises
Ziele
Nach dieser Lektion sollten Sie:
- in der Lage sein, das Erzeuger- und Verbraucherbezugspfeilsystem anwenden und unterscheiden zu können.
Im Kapitel Grundlagen wurde bereits der konventionelle (=dem Konventionen entsprechende) Richtungssinn von Strömen und Spannungen besprochen. Leider ist bei vermaschten Netzen häufig vor der Berechnung nicht überschaubar in welche Richtung der konventionelle Richtungssinn aller Ströme und Spannungen verläuft.
in Abbildung 5 ist ein solches vermaschtes Netz gezeigt. In dieser Schaltung ist ein Schalter $S_1$ und ein Strom $I_2$ gekennzeichnet.
Wird über den Schalter $S_1$ der Widerstand gewechselt, so ändert sich die Richtung des Stroms $I_2$
Merke:
- Vor der Berechnung werden die Bezugspfeile für Ströme und Spannungen beliebig festgelegt
- Nach der Berechnung bedeutet
- $I>0$: Der Bezugspfeil gibt den konventionellen Richtungssinn des Stroms wider
- $I<0$: Der Bezugspfeil zeigt in die Gegenrichtung zum konventionellen Richtungssinn des Stroms
- Bezugspfeile des Stroms werden nach Möglichkeit in den Leitungszug gezeichnet.
Erzeuger- und Verbraucher(bezugs)pfeilsysteme
Erzeugerpfeilsystem
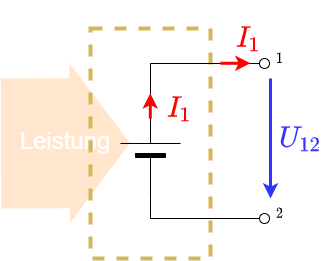
Bei Quellen (oder Erzeugern) wird aus der Umgebung Energie entnommen und dem Stromkreis zur Verfügung gestellt.
Bei Erzeugern hängt der Pfeilfuß des Stromes an Pfeilspitze der Spannung. Spannungs- und Strompfeil sind antiparallel ($\uparrow \downarrow$).
Für Erzeuger gilt:
$P_{1} = U_{12} \cdot I_1 \stackrel{!}{>} 0$
Die Leistungstransfer von der Umgebung in das Stromnetz über den Erzeuger bzw. das Erzeugerpfeilsystem wird positiv gerechnet.
Verbraucherpfeilsystem
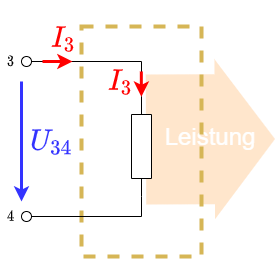
Bei Verbrauchern wird aus dem Stromkreis Energie entnommen und der Umgebung zur Verfügung gestellt.
Bei Verbrauchern hängen der Pfeilfüße bzw. Pfeilspitzen des Stromes und der Spannung zusammen. Spannungs- und Strompfeil sind parallel ($\uparrow \uparrow$).
Für Verbrauchern gilt:
$P_{3} = U_{34} \cdot I_3 \stackrel{!}{>} 0$
Die Leistungstransfer vom Stromnetz in die Umgebung über den Verbraucher bzw. das Verbraucherpfeilsystem wird auch positiv gerechnet.
Das Zählpfeilsystem
2.3 Knoten, Zweige und Maschen
Erklärung der verschiedenen Netzwerkstrukturen
(Graphen und Bäume werden erst in späteren Kapiteln benötigt)
Ziele
Nach dieser Lektion sollten Sie:
- in einer Schaltung die Knoten, Zweige und Maschen identifizieren können.
- eine Schaltung damit übersichtlicher darstellen können.
Elektrische Stromkreise haben typischerweise die Struktur von Netzen. Netze bestehen aus zwei elementaren Strukturelementen:
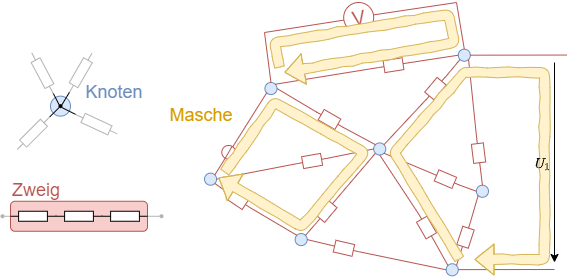
- Zweige/Kanten: Verbindungen zwischen zwei Knoten
- Knoten: Verbindungspunkte mehrerer Zweige
Bei elektrischen Schaltkreisen ist zu beachten:
- Zweige beinhalten mindestens ein Bauteil.
- Knoten verbinden mehr als zwei Zweige und können auch räumlich ausgedehnt sein.
Zweige in elektrischen Netzwerken bezeichnet man als Zweipole. Ihr Verhalten wird durch Strom-Spannungs-Kennlinien beschrieben und im Kapitel Lineare Quellen und Zweipole näher erklärt.
Zudem soll noch ein weiterer Begriff erklärt werden:
Eine Masche ist ein geschlossener Weg im Netz. Das heißt eine Masche beginnt und endet am gleichen Knoten und läuft über mindestens einen weiteren Knoten.
Da auch ein Voltmeter als Komponente zwischen zwei Knoten vorhanden sein kann, ist es auch möglich eine Masche über eine Angabe einer Spannung zu schließen (vgl. $U_1$ in Abbildung 10).
Im Gegensatz zu den anderen Ursache-Wirkungs-Beziehungen ändert sich bei den vernetzten Stromkreisen fast immer das gesamte Verhalten, wenn in einem Zweig / an einem Knoten eine Änderung auftritt.
Dies ist vergleichbar mit anderen Änderungen in anderen Netzen, z.B. einem Stau im Straßennetz, aufgrund dessen andere Straßen eine höhere Belastung erfahren. Für die Elektrotechnik bedeutet dies, dass bei sich ändernde Schaltungen eine Ermittlung der Zusammenhänge (Formeln, Strom-Spannungs-Kennlinien) häufig im Vordergrund steht und nicht ein einzelner Zahlenwert.
Vereinfachungen
Mit der Kenntnis von Knoten, Zweigen und Maschen lassen sich Schaltungen vereinfachen. Schaltungen lassen sich beliebig umformen, solange nach der Umformung alle Zweige an den gleichen Knoten bleiben Die Abbildung 11 zeigt wie eine solche Umformung möglich ist.
Bei praktischen Aufgaben kann ein wiederholtes Ausprobieren sinnvoll sein. Wichtig dabei ist eine nachträgliche Kontrolle, dass an jedem Knoten die selben Komponenten wie vor der Umwandlung angeschlossen sind.
Weitere Beispiele sind in folgendem Video zu finden
Aufgabe 2.3.1 Zweige und Knoten
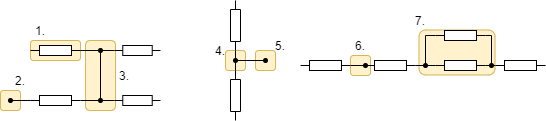
Geben Sie für die Markierungen in den Schaltkreisen in Abbildung 12 an, ob es sich um einen Zweig, einen Knoten oder weder noch handelt.
Aufgabe 2.3.2 Vereinfachungen von Schaltungen
Vereinfachen Sie die Schaltungen in Abbildung 13.
2.4 Kirchhoffsche Gleichungen
Darstellung und Anwendung der Kirchhoffschen Gesetze
Ziele
Nach dieser Lektion sollten Sie:
- die Kirchhoffschen Gleichungen bzw. Knoten- und Maschensatz kennen und anwenden können.
Der Knotensatz (1. Kirchhoffsche Gleichung)
Der Knotensatz formuliert in der Sprache der Mathematik die Erfahrung, dass sich in elektrischen Leitern keine Ladungs„anhäufungen“ auftreten. Dies ist von besonderer Relevanz an einem Netzknoten (Abbildung 14). Zur Formulierung der Gleichung werden bei diesem Netzknoten die Bezugspfeile der Ströme alle in gleicher Weise festgelegt. Das heißt: alle zeigen vom Knoten weg oder auf ihn zu.
Merke:
Die Summe aller Ströme, welche aus den Knoten zulaufen, muss Null sein.
$\boxed{I_1 + I_2 + I_3 + ... + I_n = \sum_{x=1}^{n} I_x=0}$
Es gilt von nun an folgende Festlegung:
- Ströme, deren Strompfeile auf den Knoten hin zeigen, werden in der Rechnung addiert.
- Ströme, deren Strompfeile vom Knoten weg zeigen, werden in der Rechnung subtrahiert.
Parallelschaltung von Widerständen
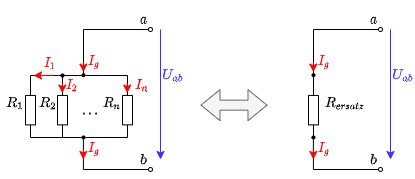
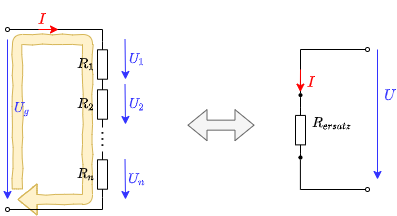
Aus dem Knotensatz lässt sich der Gesamtwiderstand für parallel geschaltete Widerstände herleiten (Abbildung 15):
Da an allen Widerständen die gleiche Spannung $U_{ab}$ abfällt, gilt mit dem Knotensatz:
$\large{{U_{ab}}\over{R_1}}+ {{U_{ab}}\over{R_2}}+ ... + {{U_{ab}}\over{R_n}}= {{U_{ab}}\over{R_{ersatz}}}$
$\rightarrow \large{{{1}\over{R_1}}+ {{1}\over{R_2}}+ ... + {{1}\over{R_n}}= {{1}\over{R_{ersatz}}} = \sum_{x=1}^{n} {{1}\over{R_x}}}$
Bei parallel geschalteten Widerständen ergibt sich also der Leitwert $G_{ersatz}$ als Summe der Einzelleitwerte: $G_{ersatz} = \sum_{x=1}^{n} {G_x}$
Allgemein gilt: Der Ersatzwiderstand einer Parallelschaltung ist stets kleiner als der kleinste Widerstand.
Speziell für zwei parallele Widerstände $R_1$ und $R_2$ gilt: $R_{ersatz}= \large{{R_1 \cdot R_2}\over{R_1 + R_2}}$
Stromteiler
Herleitung des Stromteilers mit weiteren Betrachtungen
Aus dem Knotensatz lässt sich auch die Stromteiler-Regel herleiten.
Diese besagt, dass sich bei parallel geschalteten Widerständen $R_1, ... R_n$ deren Ströme $I_1, ... I_n$ sich gerade so verhalten wie die Leitwerte $G_1, ... G_n$ durch welche sie fließen.
$\large{{I_1}\over{I_g}} = {{G_1}\over{G_g}}$
$\large{{I_1}\over{I_2}} = {{G_1}\over{G_2}}$
Aufgabe 2.4.1 Stromteiler
In der Simulation in Abbildung 16 ist ein Stromteiler zu sehen. Die Ströme verhalten sich dort gerade umgekehrt proportional zu den durchflossenen Widerständen.
- Welche Ströme erwarten Sie in den einzelnen Zweigen, wenn die Eingangsspannung von $5V$ auf $3,3V$ gesenkt würde? Nachdem Sie Ihr Ergebnis überlegt hatten, können Sie durch Bewegen des Sliders
Spannung(unten rechts neben der Simulation) entsprechend einstellen. - Überlegen Sie sich was passiert wenn Sie den Schalter umlegen würden, bevor Sie den Schalter umlegen.
Wie lässt sich, nachdem Sie den Schalter umgelegt haben, der Strom in dem Zweig erklären?
Aufgabe 2.4.2 zwei Widerstände
Zwei Widerstände von $18\Omega$ und $2 \Omega$ sind parallel geschalten. Der Gesamtstrom die Widerstände liegt bei $3A$.
Berechnen Sie den Gesamtwiderstand und die Stromaufteilung.
Der Maschensatz (2. Kirchhoffsche Gleichung)
Auch der Maschensatz beschreibt in in der mathematischen Sprache eine praktischer Erfahrung: Zwischen zwei Punkten $a$ und $b$ eines Netzwerks ergibt sich nur eine Potentialdifferenz. Die Potentialdifferenz ist damit insbesondere unabhängig davon auf welchem Weg ein Netzwerk zwischen den zwei Punkten $1$ und $2$ durchlaufen wird. Dies lässt sich durch die Betrachtung von Maschen beschreiben.
Merke:
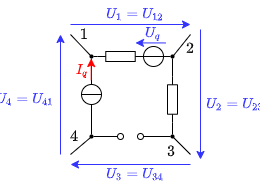
In jeder beliebigen Masche eines elektrischen Netzwerks ist die Summe aller Spannungen gleich null (Abbildung 17):
$\boxed{U_{1} + U_{2} + ... + U_{n} = \sum_{x=1}^{n} U_x = 0}$
Zur Berechnung muss ein Umlaufsinn festgelegt werden. Diese kann zunächst beliebig gewählt werden. Es gilt dann aber folgende Festlegung:
- Spannungen, deren Spannungspfeile im Umlaufsinn zeigen, werden in der Rechnung addiert.
- Spannungen, deren Spannungspfeile gegen Umlaufsinn zeigen, werden in der Rechnung subtrahiert.
Beweis des Maschensatzes
Drückt man die Spannungen in Abbildung 17 durch die Potentiale in den Knotenpunkten aus, so ergibt sich:
$U_{12}= \varphi_1 - \varphi_2 $
$U_{23}= \varphi_2 - \varphi_3 $
$U_{34}= \varphi_3 - \varphi_4 $
$U_{41}= \varphi_4 - \varphi_1 $
Werden diese Spannungen in die Maschengleichung eingesetzt, so wird
$U_{12}+U_{23}+U_{34}+U_{41} = 0$
Reihenschaltung von Widerständen
Über den Maschensatz lässt sich der Gesamtwiderstand einer Reihenschaltung (<imref BildNr13>) leicht ermitteln:
$U_1 + U_2 + ... + U_n = U_g$
$R_1 \cdot I_1 + R_2 \cdot I_2 + ... + R_n \cdot I_n = R_{ersatz} \cdot I $
Da bei der Reihenschaltung der Strom durch alle Widerstände gleich sein muss - also $I_1 = I_2 = ... = I$ - ergibt sich:
$R_1 + R_2 + ... + R_n = R_{ersatz} = \sum_{x=1}^{n} R_x $
Allgemein gilt: Der Ersatzwiderstand einer Reihenschaltung ist stets größer als der größte Widerstand.
Aufgabe 2.4.3 drei Widerstände
Gegeben sind drei gleiche Widerstände mit je $20k\Omega$.
Welche Werte sind durch beliebige Verschaltung von einem bis drei Widerstände realisierbar?
2.5 unbelasteter und belasteter Spannungsteiler
Der unbelastete Spannungsteiler
Herleitung des unbelasteten Spannungsteilers
Ziele
Nach dieser Lektion sollten Sie:
- den belasteten und unbelasteten Spannungsteiler auseinanderhalten können.
- die Unterschiede zwischen belasteten und unbelasteten Spannungsteiler beschreiben können.
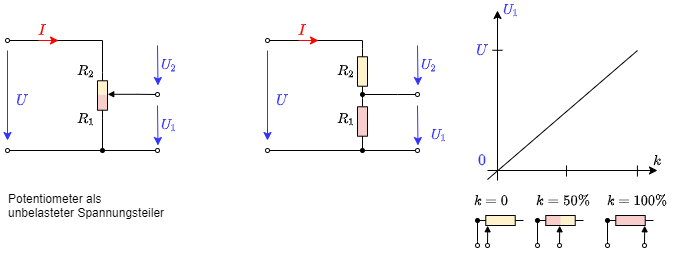
Speziell die Hintereinanderschaltung von zwei Widerständen $R_1$ und $R_2$ soll nun näher betrachtet werden. Diese Situation tritt in vielen praktischen Anwendungen auf (z.B. Potentiometer). In Abbildung 19 ist diese Schaltung dargestellt.
Über die Maschengleichung ergibt sich
$\boxed{ {{U_1}\over{U}} = {{R_1}\over{R_1 + R_2}} }$
Das Verhältnis $k={{R_1}\over{R_1 + R_2}}$ entspricht auch der Position an einem Potentiometer.
Aufgabe 2.5.1 unbelasteter Spannungsteiler
In der Simulation in Abbildung 20 ist ein unbelasteter Spannungsteiler in Form eines Potentiometers zu sehen. Die ideale Spannungsquelle stellt $5V$ bereit. Das Potentiometer hat einen Gesamtwiderstand von $1K\Omega$. In der dargestellten Konfiguration ist dieser auf $500 \Omega$ und $500 \Omega$ ausgeteilt.
- Welche Spannung
U_outerwarten Sie, wenn der Schalter geschlossen würde? Nachdem Sie Ihr Ergebnis überlegt hatten, können Sie dieses durch Schließen das Schalters überprüfen. - Überlegen Sie sich zunächst was passiert wenn Sie durch Verschieben des Schleifers („Zwischenabgriff“) die Aufteilung der Widerstände verändern würden?
Durch den Slider unten rechts neben der Simulation lässt sich Ihre Vermutung überprüfen. - Bei welcher Stellung erhalten Sie ein
U_outvon $3,5V$?
Der belastete Spannungsteiler
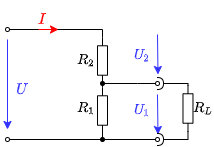
Wird - im Gegensatz zum obigen, unbelasteten Spannungsteiler - an den Ausgangsklemmen eine Last $R_L$ angeschlossen (Abbildung 21), so beeinflusst diese die Ausgangsspannung.
Durch eine Schaltungsanalyse ergibt sich:
$ U_1 = \LARGE{{{U} \over {1 + {{R_2}\over{R_L}} + {{R_2}\over{R_1}} }} }$
bzw. an einem Potentiometer mit $k$ und $R_s = R_1 + R_2$:
$ U_1 = \LARGE{{{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}} }} }$
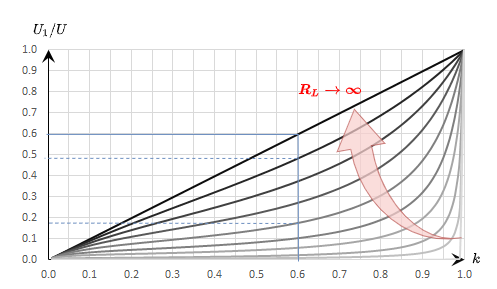
Abbildung 22 zeigt in welchem Verhältnis die ausgegebene Spannung $U_1$ zur eingehenden Spannung $U$ steht (y-Achse), in Bezug zum Verhältnis $k={{R_1}\over{R_1 + R_2}}$. Prinzipiell gleicht dies der Abbildung 19, hat aber hier noch eine weitere Dimension: Es sind mehrere Graphen eingezeichnet. Diese unterscheiden sich um das Verhältnis ${{R_s}\over{R_L}}$.
Was sagt dieses Diagramm nun aus? Dies soll an einem Beispiel gezeigt werden. Zunächst wird angenommen, dass ein unbelasteter Spannungsteiler mit $R_2 = 4 k\Omega$ und $R_1 = 6 k\Omega$, sowie eine Eingangsspannung von $10V$ vorliegt. Damit ist $k = 0,6$, $R_s = 10k\Omega$ und $U_1 = 6V$.
Nun wird dieser Spannungsteiler mit einem Lastwiderstand belastet. Liegt dieser bei $R_L = R_1 = 10 k\Omega$, so reduziert sich $k$ auf etwa $0,48$ und $U_1$ auf $4,8V$ - die Ausgangsspannung bricht also ein. Bei $R_L = 4k\Omega$ wird $k$ noch kleiner zu $k=0,375$ und $U_1 = 3,75V$. Ist die Last $R_L$ nur noch ein Zehntel des Widerstandes $R_s=R_1 + R_2$, so wird $k=0,18$ und $U_1=1,8V$. Aus der Ausgangspannung des unbelasteten Spannungsteilers ($6V$) wurde damit weniger als ein Drittel.
Aufgabe 2.5.2 belasteter Spannungsteiler
Ermitteln Sie aus der Schaltung in Abbildung 21 die obige Gleichung $ U_1 = {{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}}}}$ mit $k={{R_1}\over{R_1 + R_2}}$ und $R_s = R_1 + R_2$.
Aufgabe 2.5.3 belasteter Spannungsteiler
In der Simulation in Abbildung 23 ist ein belasteter Spannungsteiler in Form eines Potentiometers zu sehen. Die ideale Spannungsquelle stellt $5V$ bereit. Das Potentiometer hat einen Gesamtwiderstand von $1K\Omega$. In der dargestellten Konfiguration ist dieser auf $500 \Omega$ und $500 \Omega$ ausgeteilt. Der Lastwiderstand hat eine Größe von $R_L = 1 k\Omega$.
- Welche Spannung
U_OUTerwarten Sie, wenn der Schalter geschlossen würde? Hier müssen Sie etwas rechnen! Nachdem Sie Ihr Ergebnis berechnet hatten, können Sie dieses durch Schließen das Schalters überprüfen. - Bei welcher Aufteilung erhalten Sie $3,5V$. Ermitteln Sie das Ergebnis zunächst zur eine Rechnung.
Überprüfen sie es anschließend durch Verschieben des Slider unten rechts neben der Simulation.
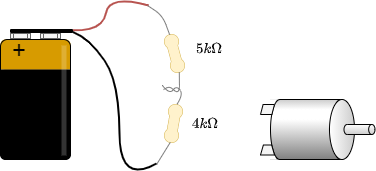
Aufgabe 2.5.4 Anwendung des belasteten Spannungsteilers - Motor
Sie wollten einen Kleinstmotor für einen kleinen Roboter testen. Anhand des Maximalstroms und des Innenwiderstands ($R_M = 5\Omega$) errechnen Sie, dass dieser mit maximal $U_{M,max}=4V$ betrieben werden kann. Ein Kollege meinte, dass Sie $4V$ über den Aufbau in Abbildung 24 aus einer $9V$-Block Batterie erhalten können.
- Berechnen Sie zunächst den Maximalstrom $I_{M,max}$ des Motors.
- Zeichnen Sie die entsprechende elektrische Schaltung mit angeschlossenem Motor als ohmschen Widerstand.
- Beim Maximalstrom soll der Motor ein Drehmoment von $M= 100mNm$ abgeben können. Welches Drehmoment würde der Motor abgeben, wenn Sie den Aufbau so umsetzen? (Annahme: Das Drehmoment des Motors steigt proportional zum Motorstrom).
- Wie könnte ein Aufbau mit Potentiometer aussehen, mit dem man tatsächlich eine Spannung zwischen $0,5V$ bis $4V$ am Motor einstellen kann? Welchen Widerstandswert muss das Potentiometer haben?
- Bauen Sie Ihre Schaltung in untenstehender Simulation auf und testen Sie diese. Eine Einführung zur Online-Simulation finden Sie unter: Online Circuit Simulator.
Für diesen Aufbau benötigen Sie im wesentlichen folgende Tipps:- Das Verlegen von Verbindungen lässt sich über das Menü
Zeichnen » Verbindung einfügen (wire)aktivieren. Anschließend muss auf den Startpunkt geklickt und anschließend bis zum Endpunkt gezogen werden. - Beachten Sie, dass Verbindungen immer nur an Verbindungspunkten angeschlossen werden können. Der rot markierte Knoten am $5 \Omega$-Widerstand zeigt an, dass dieser nicht verbunden ist. Dieser könnte im ein Rasterschritt nach links verschoben werden, da dort ein Verbindungspunkt liegt.
- Mit Druck auf die
<ESC>Taste lässt sich das Einfügen von Komponenten deaktivieren. - Mit Rechtsklick auf eine Komponente lässt sich diese kopieren oder Werte wie der Widerstand über
Bearbeiten…ändern.
Aufgabe 2.5.5 Beispiele der Berechnung von belasteten Spannungsteilern
Spannungsteiler, Vorwiderstand (Längswiderstand) und Nebenwiderstand
Übung zum Spannungsteiler
Aufgabe 2.5.6 Beispiel eines belasteten Spannungsteiler: Erklärung ohne Rechnung
2.6 Stern-Dreieck-Schaltung
Ziele
Nach dieser Lektion sollten Sie:
- dreieckige Maschen in eine Sternform (und umgekehrt) umwandeln können
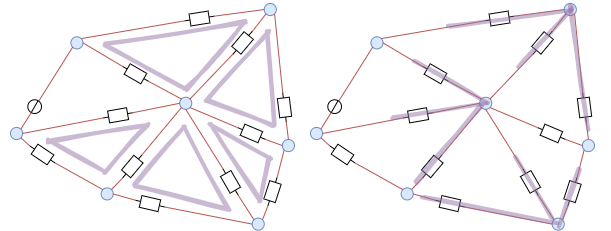
Zu Beginn des Kapitels wurde ein Beispiel eines Netzwerks gezeigt (Abbildung 1). Dabei kommt man aber mit dem Knoten- und Maschensatz nicht unmittelbar zur Lösung. Jedoch ist nach sichtbar, dass dort viele dreieckförmige Maschen bzw. sternförmige Knoten vorhanden sind (Abbildung 26). Auf diese soll nun tiefer eingegangen werden.
Dazu zunächst ein Resume aus den bisherigen Erkenntnissen. Über den Knoten- und Maschensatz wurde klar, dass sowohl aus einer Reihen-, als auch aus einer Parallelschaltung ein Ersatzwiderstand ermittelt werden kann. Betrachtet man den Ersatzwiderstand als eine Blackbox - d.h. der innere Ausbau ist unbekannt - so könnte dieser also durch beide Schaltungsarten interpretiert werden (Abbildung 27).
Wie hilft uns das nun im Falle einer dreieckförmigen Masche?
Auch in diesen Fall kann man eine Blackbox bereitstellen. Diese müsste sich aber immer gleich verhalten, wie die dreieckförmige Masche, also beliebige, angelegte Spannungen sollten gleiche Ströme erzeugen.
Anders gesagt: Die zwischen zwei Klemmen messbaren Widerständen müssen für beide Schaltungen identisch sein.
Dazu sollen nun die verschiedenen Widerstände zwischen den einzelnen Knoten $a$, $b$ und $c$ betrachtet werden, siehe Abbildung 28. Es soll herausgefunden werden wie aus einer Stern-Schaltung eine Dreieck-Schaltung entwickelt werden kann (und umgekehrt).
Abb. 28: Stern-Dreieck-Transformation
Berechung der Umformungsformeln: Sternschaltung in Dreiecksschaltung
Dreieckschaltung
Bei der Dreieckschaltung sind die 3 Widerstände $R_{ab}^1$, $R_{bc}^1$ und $R_{ca}^1$ in einer Masche verschalten.
Für die Widerstände zwischen den zwei Anschlüssen (z.B. $a$ und $b$) wird die dritte ($c$) als nicht angeschlossen betrachtet. Damit ergibt sich eine Parallelschaltung des direkten Dreieckswiderstands $R_{ab}^1$ mit der Reihenschaltung der anderen beiden Dreieckswiderstände $R_{ca}^1 + R_{bc}^1$:
$R_{ab} = R_{ab}^1 || (R_{ca}^1 + R_{bc}^1) $
$R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + (R_{ca}^1 + R_{bc}^1)}} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} $
Gleiches gilt für die anderen Anschlüssen. Damit ergibt sich:
\begin{align*} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \tag{2.6.1} \end{align*}
Sternschaltung
Die Widerstände zwischen den Anschlüssen müssen nun denen bei der Sternschaltung gleichen. Auch bei der Sternschaltung sind 3 Widerstände verschalten, diese aber in Sternform. Die Sternwiderstände sind also alle mit einem weiteren Knoten $0$ in der Mitte verbunden: $R_{a0}^1$, $R_{b0}^1$ und $R_{c0}^1$
Auch hier wird vorgegangen wie bei der Dreieckschaltung: der Widerstand zwischen zwei Anschlüssen (z.B. $a$ und $b$) wird ermittelt, der weitere Anschluss ($c$) wird als offen betrachtet. Der Widerstand des weiteren Anschlusses ($R_{c0}^1$) ist nur an einer Seite angeschlossen. Dadurch fließt durch diesen kein Strom - er ist damit nicht zu berücksichtigen. Es ergibt sich:
\begin{align*} R_{ab} = R_{a0}^1 + R_{b0}^1 \\ R_{bc} = R_{b0}^1 + R_{c0}^1 \\ R_{ca} = R_{c0}^1 + R_{a0}^1 \tag{2.6.2} \end{align*}
Aus den Gleichungen $(2.6.1)$ und $(2.6.2)$ erhält man:
\begin{align} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{a0}^1 + R_{b0}^1 \tag{2.6.3} \end{align} \begin{align} R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{b0}^1 + R_{c0}^1 \tag{2.6.4} \end{align} \begin{align} R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{c0}^1 + R_{a0}^1 \tag{2.6.5} \end{align}
Die Gleichungen $(2.6.3)$ bis $(2.6.5)$ lassen sich nun so geschickt zusammenfassen, dass auf einer Seite nur noch ein Widerstand steht.
Eine Variante ist die Formeln als ${{1}\over{2}} \cdot \left( (2.6.3) + (2.6.4) - (2.6.5) \right)$ bzw. ${{1}\over{2}} \cdot \left(R_{ab} + R_{bc} - R_{ca}\right)$ zu kombinieren. Damit ergibt sich $R_{b0}^1$
\begin{align*} {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} + {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} - {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( R_{a0}^1 + R_{b0}^1 + R_{b0}^1 + R_{c0}^1 - R_{c0}^1 - R_{a0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)} + {R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)} - {R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( 2 \cdot R_{b0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 R_{ca}^1 + R_{ab}^1 R_{bc}^1 + R_{bc}^1 R_{ab}^1 + R_{bc}^1 R_{ca}^1 - R_{ca}^1 R_{bc}^1 - R_{ca}^1 R_{ab}^1}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{1}\over{2}} \cdot \left( {{ 2 \cdot R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{ R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} &= R_{b0}^1 \\ \end{align*}
Auf ähnlichem Weg kann man nach $R_{a0}^1$ und $R_{c0}^1$, sowie mit etwas abgewandeltem Ansatz auch auf $R_{ab}^1$, $R_{bc}^1$ und $R_{ca}^1$ auflösen.
Stern-Dreieck-Transformation
Merke:
Soll von einer Dreieckschaltung in eine Sternschaltung umgewandelt werden, so sind die Sternwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{an Anschluss x} \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Produkt der} \\ \text{am Anschluss x liegenden} \\ \text{Dreieckwiderstände} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller} \\ \text{Dreieckwiderstände} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{a0}^1 &= {{ R_{ca}^1 \cdot R_{ab}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{b0}^1 &= {{ R_{ab}^1 \cdot R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{c0}^1 &= {{ R_{bc}^1 \cdot R_{ca}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \end{align*}
Soll von einer Sternschaltung in eine Dreieckschaltung umgewandelt werden, so sind die Dreieckwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Dreieckwiderstand} \\ \text{zwischen den} \\ \text{Anschlüssen x und y } \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller Produkte} \\ \text{zwischen zwei} \\ \text{unterschiedlichen Sternwiderständen} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{gegenüber von x und y} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{ab}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{c0}^1}} \\ R_{bc}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{a0}^1}} \\ R_{ca}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{b0}^1}} \end{align*}
Aufgabe 2.6.1 Anwendung der Dreieck-Stern-Umwandlung
Aufgabe 2.6.2 schwierigere Aufgabe mit Stern-Dreieck-Umwandlung
2.7 Gruppenschaltung von Widerständen
Ziele
Nach dieser Lektion sollten Sie:
- Schaltungen, welche nur aus Widerständen bestehen, vereinfachen können.
- die Spannungen und Ströme in Schaltungen mit einer Spannungsquelle und mehreren Widerständen berechnen können.
- symmetrische Schaltungen vereinfachen können.
In diesem Unterkapitel wird auf eine Methodik eingegangen, welche beim Umformen von Schaltungen helfen soll. In Unterkapitel 2.6 Stern-Dreieck-Schaltung wurde gegen Ende bereits ein Netzwerk so umgeformt, dass es keine dreieckigen Maschen mehr enthält. Nun soll dieses Vorgehen systematisiert werden. Ausgangspunkt sind Aufgaben, bei denen für ein Widerstandsnetzwerk der Gesamtwiderstand, Gesamtstrom oder die Gesamtspannung berechnet werden muss.
einfaches Beispiel
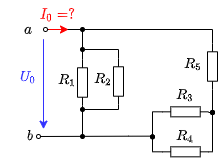
Ein Beispiel für eine solche Schaltung ist in Abbildung 29 gegeben. Hier ist $I_0$ gesucht. Dieser Strom kann über die (gegebene) Spannung $U_0$ und den Gesamtwiderstand zwischen den Klemmen $a$ und $b$ ermittelt werden. Gesucht ist also $R_{ab}$.
Wie bereits in den vorherigen Unterkapitel beschrieben, können hier auch Teilschaltung schrittweise in Ersatzwiderstände umgewandelt werden. Wichtig dabei ist, dass diese Teilschaltungen zur Umwandlung in Ersatzwiderstände immer nur zwei Anschlüsse (= zwei Knoten zur „Außenwelt“) haben dürfen.
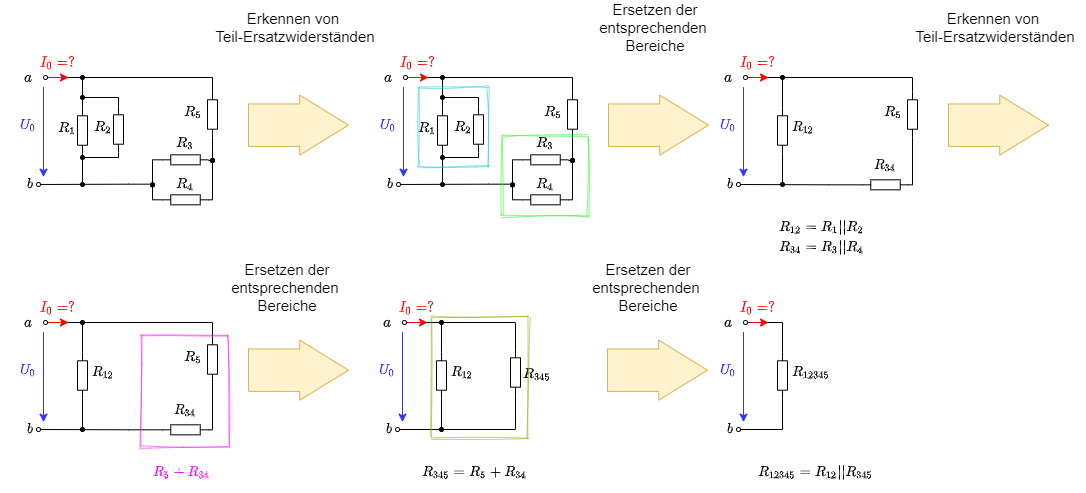
Abbildung 30 zeigt die schrittweise Umwandlung der Ersatzwiderstände an diesem Beispiel.
Als Ergebnis des Ersatzwiderstands erhält man:
\begin{align*} R_g = R_{12345} &= R_{12}||R_{345} = R_{12}||(R_3+R_{45}) = (R_1||R_2)||(R_3+R_4||R_5) \\ &= {{ {{R_1 \cdot R_2}\over{R_1 + R_2}} \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) }\over{ {{R_1 \cdot R_2}\over{R_1 + R_2}} +R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}} }} \quad \quad \quad \quad \quad \quad \bigg\rvert \cdot{{(R_1 + R_2) \cdot (R_4 + R_5)}\over{(R_1 + R_2) \cdot (R_4 + R_5)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) \cdot (R_4 + R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 \cdot (R_4 + R_5) + R_4 \cdot R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ \end{align*}
Beispiel mit Dreieck-Stern-Transformation
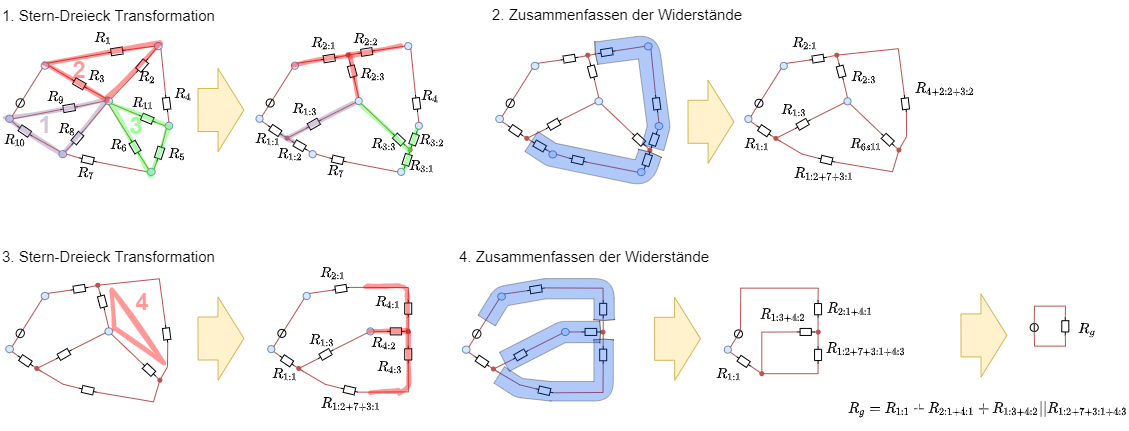
Mit der Dreieck-Stern-Transformation lässt sich nun auch das anfängliche Beispiel umwandeln. Bei komplizierteren Schaltungen ist die wiederholte Dreieck-Stern-Transformation mit anschließendem Zusammenfassen der Widerstände sinnvoll, solange bis die entstandene Schaltung leicht mit Knoten- und Maschensatz berechenbar wird (Abbildung 31). Hier wird auf eine Rechnung verzichtet - es empfiehlt sich hier mit Zwischenergebnissen für die transformierten Widerständen zu rechnen.
Beispiel mit Symmetrien in der Schaltung
Ein gewisser Sonderfall betrifft mögliche Symmetrien in Schaltungen. Falls dies vorhanden sind, kann eine weitere Vereinfachung vorgenommen werden.
Abbildung 32 zeigt links ein symmetrischen Aufbau eines Netzwerks aus jeweils gleichen Widerständen $R$. Zum Verständnisgewinn ist in der Mitte in der gleichen Schaltung zusätzlich Schalter und Testpunkte (TP) verbaut, welche die Spannung gegen Masse anzeigen.
Über die Schalter kann nachgeprüft werden, ob ein Strom fließt, falls die jeweiligen Knoten verbunden werden. In der Simulation ist zu sehen, dass dies nicht der Fall ist. Im symmetrischen Aufbau sind diese Knoten jeweils auf dem gleichen Potential.
Damit lässt sich die Schaltung auch in die Form bringen, wie sie in Abbildung 32 rechts zu sehen ist. Diese Schaltung ist wiederum leicht berechenbar:
\begin{align*} R_g = R || R + R || R || R || R + R || R || R || R + R || R = {{1}\over{2}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{2}}\cdot R = 1,5\cdot R \end{align*}
Aufgabe 2.7.1 Aufgabe zur Schaltungsvereinfachung I
Aufgabe 2.7.2 Aufgabe zur Schaltungsvereinfachung II + III
Aufgabe 2.7.3 Aufgabe zur Schaltungsvereinfachung IV
Aufgabe 2.7.4 Aufgabe zur Schaltungsvereinfachung IV
Aufgabe 2.7.5 Aufgabe zur Schaltungsvereinfachung V
Aufgabe 2.7.6 Aufgabe zur Schaltungsvereinfachung VI
Aufgabe 2.7.7 Vereinfachen von Schaltungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
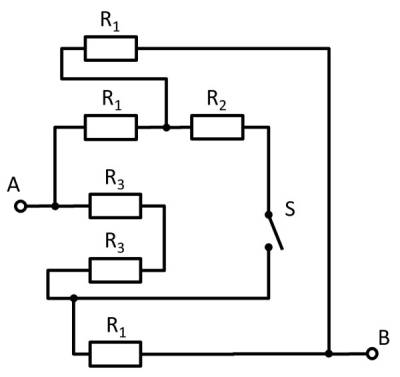
Gegeben ist die nebenstehende Schaltung mit
$R_1=10 \Omega$
$R_2=20 \Omega$
$R_3=5 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Der Schalter sollt dabei durch eine offene Leitung ersetzt werden.
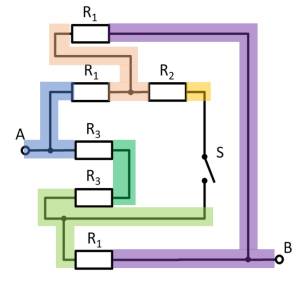
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
Es ergibt sich somit:
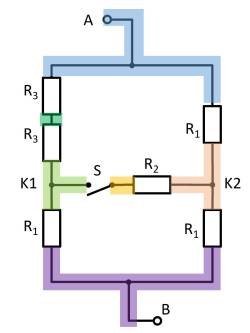
Damit lassen sich $R_3$ und $R_3$ zu $R_{33} = 2 \cdot R_3 = R_1$ zusammenfassen und es ergibt sich so ein linker und ein rechter Spannungsteiler.
Nun ist sichtbar, dass sich im linken und rechten Spannungsteiler das gleiche Potential am jeweiligen Abzweig, bzw. am Knoten K1 (grün) und K2 (pink).
Der Gesamtwiderstand lässt sich also berechnen als $R_{ges} = (2 \cdot R_1)||(2 \cdot R_1)$.
Durch die Symmetrie können aber auch die Knoten K1 und K2 kurzgeschlossen werden. Es gilt also auch $R_{ges} = 2 \cdot \left( R_1||R_1 \right)$.
2. Welcher Gesamtwiderstand ergibt sich, wenn Schalter $S$ geschlossen wird?
Der Widerstand bleibt also gleich.
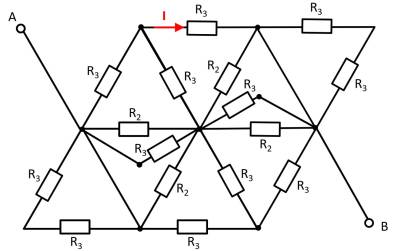
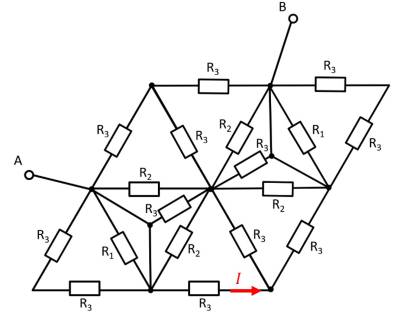
Aufgabe 2.7.8: Vereinfachen von Schaltungen II (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$R_2=10 \Omega$
$R_3=20 \Omega$
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Schalter (falls vorhanden) sollten dabei durch eine offene oder kurzgeschlossene Leitung ersetzt werden.
- Ergeben sich gleiche Potentiale an verschiedenen Knoten, die geschickt genutzt werden können?
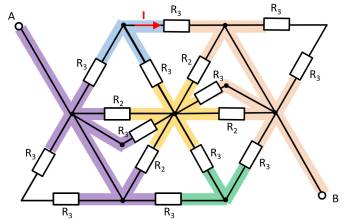
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
Es zeigt sich, dass die beiden Widerstände $R_3$ oben links und unten rechts jeweils kurzgeschlossen sind. Es ergibt sich somit:
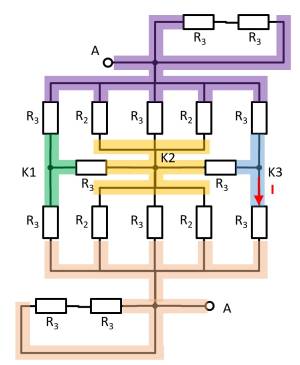
Hier hilft es das Potential der Knoten K1, K2 und K3 zu betrachten. Bei K2 müssen dazu die Widerstände $R_2 || R_3 || R_2$ oben und unten jeweils zusammengefasst werden. Es ergeben sich also die gleichen Widerstandswerte oben und unten. Auch bei den Knoten K1 und K2 ergeben sich jeweils die gleichen Widerstandwerte oben wie unten. Mit den jeweils gleichen Verhältnissen der Widerstände bei K1, K2 und K3 lässt sich folgern, dass über die Widerstände $R_3$ zwischen K1 und K2 bzw. K2 und K3 kein Strom fließt. Diese tragen also nicht zum Gesamtwiderstand bei. In einem solchen Fall kann zwischen den relevanten Knoten für die Rechnung ein Kurzschluss oder eine offene Leitung frei gewählt werden. Im folgenden wird eine offene Leitung gewählt. Zusätzlich können die parallelen Stränge noch umsortiert werden.
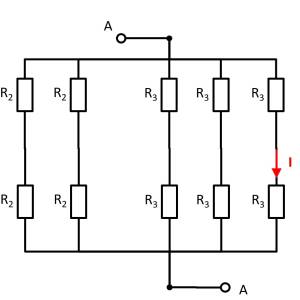
Damit ergibt sich:
\begin{align*} R_{ges} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) \quad && || \quad \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{ges} &= R_2 \quad && || \quad \frac{2}{3}\cdot R_3 \\ R_{ges} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} = \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Nun sei die Spannung von A nach B: $U_{AB}=U_0= 20 V$. Wie groß ist der Strom $I$?
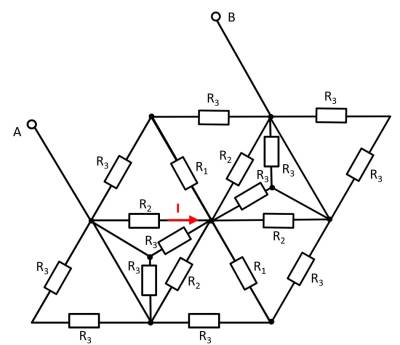
Aufgabe 2.7.9 - Variation: Vereinfachen von Schaltungen II (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
Gegeben ist die nebenstehende Schaltung mit
$R_1=10 \Omega$
$R_2=20 \Omega$
$R_3=5 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
2. Nun sei die Spannung von A nach B: $U_{AB}=U_0= 10 V$. Wie groß ist der Strom $I$?
Aufgabe 2.7.10 - Variation: Vereinfachen von Schaltungen III (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$R_2=20 \Omega$
$R_3=10 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
2. Nun sei die Spannung von A nach B: $U_{AB}=U_0= 30 V$. Wie groß ist der Strom $I$?
weitere Aufgaben
Weitere Aufgaben sind Online auf den Seiten von HErTZ zu finden (Auswahl links im Menu).