1 Boolean Algebra
1.1 Motivation: Digital Electronics in Daily Life
Learning Objectives
By the end of this section, you will be able to:
- know the Boolean functions, their notations, and truth tables.
- apply the Boolean rules of arithmetic.
- simplify Boolean expressions.
- know the following terms: (logic) gates, names of arithmetic rules.
1.1.1 Everything is one, except the zero...
Before we start to dive deeper into digital systems, it is a good idea to approach the topic with a first practical example. For this, we look at a USB cable and mentally cut the cable. We will see a total of four wires waiting for us. Two of them are called D+ and D-. These are the wires that are used for digital data transmission. With special tools - like an oscilloscope, we can measure the time course of the voltage between D+ and D-. This voltage shows two different levels and rises and falls in between. What we see are the logic states $0$ or $1$! 1)
Beyond data transmission, we can also encode other things with binary numbers: for example, we could look at
- the position of a lever - whether it is pointing up or down.
- or a switch that is open or closed.
- or a light that is on or off.
- even whether it is raining or not raining, whether a dog is barking or not barking, or other things - we can encode all of that in binary units.
In reality, the measured voltage on the USB cable would also show noise and only roughly depict the two states. When we ignore the noise and only assume that an upper level ($HIGH$ or $H$) encodes one state and the lower one ($LOW$ or $L$) the second state the diagram is also called the level diagram. In contrast to analog systems, a signal can only take one of the two valid states in digital systems. Similarly, boolean algebra only uses the states $TRUE$ and $FALSE$.
Note!
- The smallest binary message set is called a „bit“, which comes from the English term „binary digit“. A bit thus describes the logical state of a two-valued system. The binary characters can be written as, e.g.:
- $0$, $1$
- $FALSE$, $TRUE$
- $HIGH$, $LOW$
- In binary logic, every expression can only be true or false. If something is not true, it has to be false - and vice versa.
- Therefore, binary logic has some limitations for real-world applications: It may only rain softly, a light might be dimmed, and also the voltage (which represents the bit) might be in an in-between state. This situation has to be coped with beyond the binary logic. Beyond binary logic, there is often an invalid state in reality, which separates the logic states.
We will find out more of the details behind these states in the chapter Number Systems. In this chapter, we will start to think about, how these binary signals in connection with some algebra can generate a base for fundamental logic building blocks. These building blocks will be stacked together into larger boxes in the next chapters and are the basis for microcontrollers, microprocessors, and virtually all digital electronics from watches over automotive controllers to supercomputers.
 Abb. 2: Inner 'Life' of an Integrated Cicuit
Abb. 2: Inner 'Life' of an Integrated Cicuit
1.1.2 At the Heart of a Computer
 Abb. 3: A 'topless' microcontroller
Abb. 3: A 'topless' microcontroller
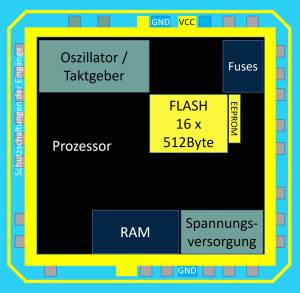
The core of a computer is the processor in which the instructions are executed. This central processing unit (CPU) is also used in microcontrollers, which can be found around us in almost every device: Mobile phones, cars, bank cards, and washing machines… Often there are even several microcontrollers installed in the devices.
In the microcontroller, in addition to the command-executing microprocessor (more precisely, the arithmetic-logic unit), other peripherals such as memory, clock generation, analog-to-digital converter, and much more are built in. This makes it a compact tool for many applications. If you look at the microcontroller under an optical microscope, you will see the following picture (Abbildung 3).
But now let's take a look at the structure of the processor. The processor shown in Abbildung 4 and Abbildung 5 were developed by two students in 1990 and consists of several tens of thousands of transistors. This chip paved the way to cheap, fast, and yet easily programmable controllers, from the fax machine to the hobby basement, and can be found on Arduino boards, among others. You will get to know and program the ATmega328 - a distant successor with several hundred thousand transistors - in higher semesters. The images depict various peripheral components: The processor, FLASH, EEPROM, and fuses will be shown in the following chapters. The voltage supply (German 'Spannungsversorung'), is needed to generate additional higher voltages based on the supplied external voltage.
The following clip shows a zoom into the smallest parts of the controller.
One question is still unclear: how can we connect the zeros and ones in such a way, that the processor can calculate something like $23 + 42$? For this, we need to have a look at binary logic.
1.2 Binary Logic
Learning Objectives
By the end of this section, you will be able to:
- know the Boolean functions, their notations, and truth tables.
- apply the Boolean rules of arithmetic.
- simplify Boolean expressions.
- understand the following terms: bit, the different (logic) gates, timing diagram, and truth table.
- understand the purpose of the Tri-State gate and the „Z“ state.
- understand the use of the „Don't care“ state.
1.2.1 First Steps into Logic
We have already learned about the 'bit', and its two-valued value. This can be connected to the ancient idea of binary logic. The Greek Philosopher Aristotle started to build up a system to conclude from statements like „at night, it is dark outside“ and „it is night“ to „it has to be dark outside“. It might seem a bit unrelated to controllers and computers, at the first sight. But in this scientific interpretation of logic, all logic statements are either true or false.
George Boole developed a more mathematical way of handline logic. Based on his work the fundamental logic was solidified into axioms. One axiom we have already seen: If something is true, it cannot be false and vice versa (the 'theorem of contradiction').
Other axioms help to combine statements. This is called 'reasoning' or 'deduction'.
- This was already used in some sentences before: If „at night, it is dark outside“ and „it is night“ is true, one can make the implication 'it has to be dark outside'.
But be aware, that this is not always reversible: It could also be a solar eclipse. - Another deduction is the equivalence: when '$A$' implies '$B$', and '$B$' implies '$A$' both statements are equivalent.
In the following, we will have a look at the basic logic combinations, which are needed for digital systems. These basic logic combinations of logic statements (or bits) are called logic operators and can be used similarly to the algebraic „plus“ or „minus“. The mathematical construct, which describes the system of these combinations is called boolean algebra. In digital systems, the logic operators can be represented as a circuit of transistors or switches. This can be black-boxed into logic gates.
These tools will get more familiar in the next subchapter.
A good introduction to binary logic
1.2.2 The logic Operator NOT
The first very simple circuit negates the input value. It is also called an inverter or negation (logic NOT, NOT gate). This logic operator always generates the output value $Y(0)=1$ from the digital input value $X=0$ and for $X=1$ correspondingly $Y(1)=0$. Abbildung 6 shows an example: The light is only on ($X=1$), when the input is off ($Y=0$) - this functionality is „hard-wired“.
When you think about the inputs and outputs in the shown picture above, you realize, that the input is a voltage, but the output is current. This is sometimes beneficial, but within digital systems commonly only voltages are used.
To control an (output) voltage with an (input) voltage two complement types of switches are combined similar to a voltage divider or a half-bridge (see Abbildung 7). One is normally open and the other one is normally closed. This can also be set up with complementary types of transistors. Thus, only one transistor (TRANSfer ResISTOR) becomes conductive at a time, the other one correspondingly high impedance.
With this setup, the logic voltages ($0~\rm V$, $5~\rm V$) are just switched complimentary via the switches. This technique is also called CMOS technique: Complementary MOSFET. In today's electronics, this technology is used throughout and has completely replaced older variants (e.g. TTL).
Comparing the circuits in Abbildung 6 and Abbildung 7, one could simply see, that double the number of switches have to be used and the lower one is a bit trickier to understand. With this in mind, for the following operators only the first type of circuit will be shown.
The circuit symbols of the NOT-gate are shown in Abbildung 8. Depending on the (software) tools and schematics one of the types is printed.
Besides the symbol other representation are also common (see also Abbildung 9):
- The truth table shows the input(s) $X$ on the left and the output(s) $Y$ on the right. There is a row for each distinct combination of inputs. This representation will get handy in the next chapters, to analyze more complex logic. Often instead they are also called look-up table or LUT.
- The timing diagram shows the sequential behavior. For this diagram, the input variables are stimulated with all possible state combinations. Also, this will become handy, especially in the chapter Sequential Logic.
- In math the inversion has also multiple representations e.g.
- $Y = /X$ (used e.g. for input with a keyboard)
- $Y = \overline{X}$ (often used when handwriting and math)
Y = !X(used in c language)
Note!
- Inputs are always denoted with $X$
- Outputs are always denoted with $Y$
- There are multiple ways for representing logic. The most common ones are:
electric circuits with switches (or transistors), logic gates, truth tables, timing diagrams, and mathematical representation. - When you use a representation: use it uniformly.
1.2.3 The logic Operator AND
The next circuit will generate a positive output only, if all inputs are true. This is called a logical conjunction (logic AND, AND gate). When one or more inputs are false the output is also false. Abbildung 10 shows an example: The light is only on ($Y=1$), when all inputs are on ($X0=1$, $X1=1$, …). This is commonly used for safety circuits, e.g. when the workspace of a robot has multiple doors and all have to be closed to start.
Again, the other representations are shown:
- The truth table and timing diagram are depicted in Abbildung 12.
- In math the AND operation has again multiple representations e.g.
- $Y = X0 * X1$ (used e.g. for input with a keyboard)
- $Y = X_0 \cdot X_1$ (often used when handwriting or in math)
Y = X0 & X1(used in c language bitwise)- $Y = X_0 \land X_1$ (used in logic)
For upcoming, more complex terms the algebraic notation ($Y = X_0 \cdot X_1$) usually leads to a better understanding.
1.2.4 The logic Operator NAND
The NOT gate is often used in front of or after other gates. When used after AND gates, this creates a 'NOT AND' or in short 'NAND' (logic NAND, NAND gate). This circuit will only generate a negative output, if all inputs are true. When one or more inputs are false the output is true. Abbildung 13 shows an example: The light is only off ($Y=0$), when all inputs are high ($X0=1$, $X1=1$, …). In the simulation one has to look in detail: the used switches are normally closed (closed when the input is low). Therefore the switches are only open when the input is high.
The circuit symbols are shown in Abbildung 14. To shorten the circuit, the NOT is often 'shrank' only to a small circle after the gate.
Again, the other representations are shown:
- The truth table and timing diagram are depicted in Abbildung 15.
- In math the NAND operation has again multiple representations e.g.
- $Y = /(X0 * X1)$ (used e.g. for input with a keyboard)
- $Y = /(X_0 \cdot X_1)$ or $Y = \overline{X_0 \cdot X_1}$ (often used when handwriting or in math)
Y = !(X0 & X1)(used in c language bitwise)- $Y = /(X_0 \land X_1)$ or $Y = \overline{X_0 \land X_1}$ (used in logic)
1.2.5 The logic Operator OR
We already had a look at the AND gate. So what about OR? Of course, there is also this kind of operation. This is called a logical disjunction (logic OR, OR gate). When there is one or more inputs true the output is also true. Abbildung 16 shows an example: The light is only off ($Y=0$), when all inputs are off ($X0=0$, $X1=0$, …). Doesn't it - at first glimpse - seem similar to the NAND circuit? The main difference is that normally open switches are used. Only, when both switches are open the light is off.
The circuit symbols are shown in Abbildung 17. The DIN symbol is derived from the fact, that one or more inputs have to be true to get a true output.
Again, the other representations are shown:
- The truth table and timing diagram are depicted in Abbildung 18.
- In math the OR operation has again multiple representations e.g.
- $Y = X0 + X1$ (used e.g. for input with a keyboard or in handwriting)
Y = X0 | X1(used in c language bitwise)- $Y = X_0 \lor X_1$ (used in logic, the $\lor$ stands for the Latin vel, which means or)
For upcoming, more complex terms the algebraic notation ($Y = X_0 + X_1$) usually leads to a better understanding. Also here: we will see the connection to math in the next chapters.
1.2.6 The logic Operator XOR
Beside the OR there is also an „either … or …, but, not both“. This is called exclusive or, in short XOR (logic XOR, XOR gate). Only when one input is true the output is true. Abbildung 16 shows an example: When none or when all inputs are on, the light is only off. The circuit looks a bit more complicated with two series branches in parallel and the use of both normally closed and normally open switches. On the other hand, one can already think, that one of the branches looks similar to the setup for the AND gate, and the parallel setup is similar to the NAND gate. Could it be possible to convert the gates into each other? We will see that next…
The circuit symbols are shown in Abbildung 20. Both symbols have similarities with the OR symbols.
Again, the other representations are shown:
- The truth table and timing diagram are depicted in Abbildung 21.
- In math the XOR operation has again multiple representations e.g.
- $Y = X0 \# X1$ (used e.g. for input with a keyboard or in handwriting)
Y = X0 ^ X1(used in c language bitwise)- $Y = X_0 ⊕ X_1$ (used in logic)
Exercise 1.2.1. NOR and XNOR
- Think about a circuit (with multiple switches and one lamp) to implement NOR and XNOR.
- What is the relation between the circuits of NOR and AND? And how about XOR and XNOR?
- What would the gate representation and the other representations look like?
1.2.7 The Tri-State Gate
The tri-state gate is not a boolean gate, however, it is still often used in logic circuits such as microcontrollers. The essence of the tri-state gate is - in short - to be able to output 'nothing'. Nothing means: neither high nor low.
One possible output of the tri-state gate - besides high and low - is 'high ohmic', which is often referred to as $Z$. In this case, the gate output is not controlled by the tri-state gate but floats. The output can instead be controlled by another external source. The main use of this gate is to disconnect one logic circuit from another one.
Abbildung 16 shows the function of a tri-state gate: When the $EN$able input is set to high this gate becomes transparent and the output $Y$ equals the input $Y$. When $EN$ is set to low, the output is not pinned to the input anymore. In the simulation above with $EN = 0$ the output voltage is clamped by the voltage behind the resistor (here $3V$). Since this voltage could be any value this output cannot be called low or high, but is called the (undefined) state $Z$.
The circuit symbol is shown in Abbildung 23. Usually, the triangle symbol is used, the DIN / EN symbol is much less common and therefore here ignored. Since the Tri-State gate is not a logical gate it does not have any mathematical representation.
In the Abbildung 24 the truth table is shown. In this case, $EN=0$ the input $X$ does not matter.
The situation 'the input x does not matter' is usually simplified by the use of a don't care term.
The 'don't care' is written down as a x or a -.
Example of an Application for a Tri-State Gate
Let's imagine, we want to connect two microcontrollers $A$ and $B$ to enable communication, i.e. transmitting and receiving data on both sides.One possibility would be to use two wires:
- One wire for data sent from $A$ to $B$
- One wire for data sent from $B$ to $A$
This is shown in Abbildung 25. You can change the inputs $X0$ and $X1$ by clicking on the L and H nearby these labels.
The big advantage of this configuration is, that both connected microcontrollers can send data whenever they want. The biggest disadvantage is, that one needs two wires.
Once we think of only using one wire, it becomes more complicated: a single wire can only be driven by one digital input - only one can transmit data at any given time.
Therefore, we have to switch on both sides from receive to transmit, e.g. by a Single Pole Double Throw switch. This can be seen in Abbildung 26 for the two situations „$A$ sends data to $B$“ and „$B$ sends data to $A$“.
Again, you can change the inputs $X0$ and $X1$ by clicking on the L and H nearby these labels.
The problem is, that at one time the output becomes an input, but boolean gates an algebra result every time in boolean outputs.
We still could try to solve it with gates, as seen in Abbildung 27: Each microcontroller has an enable signal (EN0, EN1). Both outputs from the microcontrollers have to be combined with another gate in such a way, that the result shows the enabled signal.
The problem here: We are back to a two-wire system. So, we need to „split up“ the OR gate somehow..
For this we can use the Tri-State gate: This enables us to switch output to high ohmic. This means this output does not provide any current anymore, so this output is not driven anymore.
1.3 Timing Diagram - A Deep Dive
Learning Objectives
By the end of this section, you will be able to:
- understand in which possible way the tri-state output is shown in timing diagrams
- know how the situation 'either
0or1' is shown in timing diagrams
Since the timing diagram is of importance not only for the upcoming courses like Electronics (in the 3rd semester) I recommend watching the following video sequence.
24 minutes intro into applications of the timing diagram in real data sheets (a cutout from 5:08 to 28:52 from a full video of EEVblog)
1.4 Convertibility of Gates
Learning Objectives
By the end of this section, you will be able to:
- convert simple gates into each other
- convert interconnections from a few logic gates to truth tables and vice versa.
- build-up other gates from NAND and NOR gates.
Some of the circuits in the previous chapter looked suspiciously similar. We will now have a deeper look into this and try to convert some gates into each other. In this subchapter, we will focus on combining NAND gates to build other gates. As we will see, based on the NAND and NOR gates any other gate and any other logic can be created.
1.4.1 NAND in NOT
The conversion from NAND to NOT is relatively simple: When both inputs to NAND are the same (either '1' or '0') the output will be the negation of the input. This can also be seen in the truth table of the NAND gate: when the inputs as the same only the first and last rows, have to be considered and leading to an inverting behavior.
A different approach to get a NOT is to set the second input to '1'. Here, the NOT can be 'deactivated' of with the second input. This can be tested in the Abbildung 29 by clicking on the input 'H' of the NAND gate on the right below.
1.4.2 NAND in AND
With the knowledge from 'NAND to NOT' the NAND can be converted to AND: a negated NAND leads to an AND. It is roughly similar to 'not a no-go' and is logically a 'go'. Therefore, the NOT had to be set behind the NAND.
1.4.3 NAND in OR
When each input of a NAND gate is inverted the result acts like an OR gate. To understand this, one can again look at the truth table of the NAND and the OR gate and try to investigate what happens when the inputs of the NAND are negated.
1.5 Rules for boolean Algebra
Learning Objectives
By the end of this section, you will be able to:
- know and use the arithmetic rules in boolean algebra.
We have seen, that (at least) some of the gates can be represented using others. To approach this more systematically, we will now have a look at the arithmetic rules of boolean algebra. These rules can be used to either build a logic circuit out of the basis gates shown in chapter 1.2. On the other hand, we are also able to simplify the logic circuits by these rules.
1.5.1 The Set of Rules
The following table shows the main rules which help us to generate and optimize logic expressions and circuits.
It is possible to click on „math representation“ and „algebraic representation“ to switch both.
Have a look at the algebraic representation. These are probably much simpler to remember!
Be also aware, that the logical expressions sometimes are written as $X0$, $X1$, … and sometimes with other letters, like $a$, $b$, …
math representation
| Nr | Math Term / Formula | Description |
|---|---|---|
| 1 | Closure | The operators $\land$ and $\lor$ map elements from $B=\{a,b,...,n\}$ to $B$. |
| $B \land B \rightarrow B $ | ||
| $B \lor B \rightarrow B $ | ||
| 2 | Duality | If $A$ is a statement of boolean algebra, so is $A^*$. $A^*$ is obtained by exchanging $\land$ with $\lor$ and vice versa. |
| 3 | Neutral Element | There exist a neutral element to the operators $\land$ and $\lor$. Applying the operator to a and the neutral element results in $a$. |
| $a \land 1 = a $ | ||
| $a \lor 0 = a $ | ||
| 4 | Complementary Element | There exist a complementary element to the operators $\land$ and $\lor$. The negation of $a$ is for both operators the complementary element. |
| $a \land \bar{a} = 0 $ | ||
| $a \lor \bar{a} = 1 $ | ||
| 5 | Idempotence | Applying the operators $\land$ and $\lor$ to a similar input a results in $a$. |
| $a \land a = a $ | ||
| $a \lor a = a $ | ||
| 6 | Commutative Law | Inputs $a$ and $b$ are interchangable. |
| $a \land b = b \land a $ | ||
| $a \lor b = b \lor a $ | ||
| 7 | Associative Law | For the same operator bracketing can be moved. associative means „to unite“ or „to connect“ |
| $a \land (b \land c) = (a \land b) \land c $ | ||
| $a \lor (b \lor c) = (a \lor b) \lor c $ | ||
| 8 | Distributive Law | The bracketing is similer to mathematical multiplication: $a \cdot (b + c) = (a \cdot b) + ( a \cdot c) $. However this is true for both boolean operators! |
| $a \land (b \lor c) = (a \land b) \lor (a \land c)$ | ||
| $a \lor (b \land c) = (a \lor b) \land (a \lor c)$ | ||
| 9 | Law of Absorption | In bracketed formulas similar expressions can „absorb“ each other. This law can be derived from the laws (8), (5), (7) |
| $a \land (a \lor b) = a$ $a \land (\bar{a} \lor b) = a \land b $ |
||
| $a \lor (a \land b) = a$ $a \lor (\bar{a} \land b) = a \lor b $ |
||
| 10 | DeMorgan's Rule | $\land$ can be written as $\lor$, BUT one has to negate the inputs and outputs |
| $\overline{a\land b} = \overline{\overline{\bar{a}\lor \bar{b}}} = \bar{a}\lor \bar{b} $ $ \bar{a}\lor \bar{b}= \overline{\bar{\bar{a}}\land \bar{\bar{b}}} = \overline{a\land b} $ |
||
| $\overline{a\lor b} = \overline{\overline{\bar{a}\land \bar{b}}} = \bar{a}\land \bar{b} $ $ \bar{a}\land \bar{b}= \overline{\bar{\bar{a}}\lor \bar{\bar{b}}} = \overline{a\lor b} $ |
algebraic representation
| Nr | Math Term / Formula | Description |
|---|---|---|
| 1 | Closure | The operators $\cdot$ and $+$ map elements from $B=\{a,b,...,n\}$ to $B$. |
| $B \cdot B \rightarrow B $ | ||
| $B + B \rightarrow B $ | ||
| 2 | Duality | If $A$ is a statement of boolean algebra, so is $A^*$. $A^*$ is obtained by exchanging $\cdot$ with $+$ and vice versa. |
| 3 | Neutral Element | There exist a neutral element to the operators $\cdot$ and $+$. Applying the operator to a and the neutral element results in $a$. |
| $a \cdot 1 = a $ | ||
| $a + 0 = a $ | ||
| 4 | Complementary Element | There exist a complementary element to the operators $\cdot$ and $+$. The negation of $a$ is for both operators the complementary element. |
| $a \cdot \bar{a} = 0 $ | ||
| $a + \bar{a} = 1 $ | ||
| 5 | Idempotence | Applying the operators $\cdot$ and $+$ to a similar input a results in $a$. |
| $a \cdot a = a $ | ||
| $a + a = a $ | ||
| 6 | Commutative Law | Inputs $a$ and $b$ are interchangable. |
| $a \cdot b = b \cdot a $ | ||
| $a + b = b + a $ | ||
| 7 | Associative Law | For the same operator bracketing can be moved. associative means „to unite“ or „to connect“ |
| $a \cdot (b \cdot c) = (a \cdot b) \cdot c $ | ||
| $a + (b + c) = (a + b) + c $ | ||
| 8 | Distributive Law | The bracketing is similear like for multiplication: $a \cdot (b + c) = (a \cdot b) + ( a \cdot c) $. However this is true for both boolean operators! |
| $a \cdot (b + c) = (a \cdot b) + (a \cdot c)$ | ||
| $a + (b \cdot c) = (a + b) \cdot (a + c)$ | ||
| 9 | Law of Absorption | In bracketed formulas similar expressions can „absorb“ each other. This law can be derived from the laws (8), (5), (7) |
| $a \cdot (a + b) = a$ $a \cdot (\bar{a} + b) = a \cdot b $ |
||
| $a + (a \cdot b) = a$ $a + (\bar{a} \cdot b) = a + b $ |
||
| 10 | DeMorgan's Rule | $\cdot$ can be written as $+$, BUT one has to negate the inputs and outputs |
| $\overline{a\cdot b} = \overline{\overline{\bar{a}+ \bar{b}}} = \bar{a}+ \bar{b} $ $ \bar{a}+ \bar{b}= \overline{\bar{\bar{a}}\cdot \bar{\bar{b}}} = \overline{a\cdot b} $ |
||
| $\overline{a+ b} = \overline{\overline{\bar{a}\cdot \bar{b}}} = \bar{a}\cdot \bar{b} $ $ \bar{a}\cdot \bar{b}= \overline{\bar{\bar{a}}+ \bar{\bar{b}}} = \overline{a+ b} $ |
The last 3 laws are probably kind of unintuitive. Therefore, these are shown in other representations. in the following
1.5.2 Dive into Distributive Law
The distributive law can be shown as a simple example of daily life.
When one says
"I'm happy with fries AND (a water OR a coke)"
he will be happy with
(fries AND water) OR (fries AND a coke)
Be aware, that the is no exclusiveness here. The person would also be happy with fries AND water AND a coke!
The gate representation is shown in Abbildung 32. At first glimpse, the output $Y$ of the upper circuit and the lower circuit look similar (they are indeed the same).
Also, the truth tables for the first gate ($Y'$, $Y''$, $Y'''$) and a larger truth table for all results are given.
But the conversion of the upper one to the lower one is not intuitive here. That is why the multiple representations and remembering the rules for boolean algebra are very important. Translating from one representation into another one helps to use other tools to simplify systems!
1.5.3 Dive into the Law of Absorption
We will also try to transfer the law of absorption to an example of daily life.
When one says
"I'm happy with fries OR (fries AND a coke)"
he will be happy with
fries...
No matter whether there is coke with it.
The absorption of the inverse ($a + (\bar{a} \cdot b) = a + b $) is also possible:
When one says
"I'm happy with fries OR (no fries AND a coke)"
he will be happy with
fries OR a coke
When he only gets fries the first part is true. When he only gets coke, the second part is true. When he gets both, he of course gets fries and therefore the first part is true…
The gate representation is shown in Abbildung 33. When ignoring the blinking High and Low of the lines, also here the similarity of the upper and lower circuits may be not intuitive.
1.5.4 Dive into DeMorgan's Rule
At last, let's have a look at DeMorgan's rule. The following instance shows it in daily life.
When one says
"I don't like fries AND I don't like coke"
he will be unhappy when he gets either fries, or coke, or (fries and coke).
The gate representation is shown in Abbildung 34. All four circuits show the same behavior.
On the left, the NOT gate is explicitly shown. On the right, the NOT gates are shrunk down to the circles either on the input or on the output.
The important thing about DeMorgan's rules is: any expression stays the same, when
- all parts of the expression are inverted plus
- any AND is substituted with OR plus
- any OR is substituted with AND
Important is, that also most upper expressions have to be inverted.
1.5.5 Example of a logic Simplification
1.6 Examples of Gate Circuits
1.6.1 Logic Gates with multiple Inputs
Based on the associative law, when purely AND gates or purely OR gates are stacked the inputs are interchangeable.
Therefore, this stacking can be substituted with a gate symbol with multiple inputs. The two AND gates shown in Abbildung 35 can be substituted with a single one.
The essence of the AND gate is: An AND gate - no matter how many inputs it has - will only output high when all inputs are high.
Exercise 1.6.1. Other gates with multiple inputs
- What is the essence of an OR gate? what will the truth table of an OR gate with 3 inputs look like?
- What is the essence of an XOR gate? what will the truth table of an XOR gate with 3 inputs look like? (keep in mind, that this question might have multiple answers for XOR)
1.6.2 Switchable Inverter
Sometimes it is important to switch between inverting and not inverting an output. This can be done with the XOR gate. When the $EN$ in Abbildung 36 is active, the input $X$ will be inversed.
One application for a switchable inverter would be a monochrome display, where every pixel can be set by one bit. When the display (or a small part like the cursor symbol) has to be inverted it would be great to do so with a simple gate. This can be seen in this more complex example, where the display smiley can be inverted via the XOR gate during data transmission. The other logic component in this example will be explained in the following (sub)chapters.
Another usage is the inversion of binary numbers in the arithmetic logic unit of the processor.
1.6.3 Data Valve
To deactivate a data flow a simple AND gate can be used. This is also useful for channelizing data in multiple directions.
In the upper part of Abbildung 37 a single data-valve is shown. Only when $EN=1$, then the value of the data input $X$ will set as the output $Y$.
The lower part of Abbildung 37 shows the combination of two data valves. In this circuit depending on $EN$ the output of the data input $X$ will either be $Y0$ or $Y1$. This is also visible in the truth table. The truth table can be shortened which is also shown.
1.6.4 Multiplexer and Demultiplexer
In the linked 'display example' in 1.6.2 there was a Multiplexer (MUX) and a Demultiplexer (DEMUX) visible.
A multiplexer is an electronic switcher, which has several data inputs $D0$, $D1$ … and one data output $Y$. Additionally to the data input, there are also state inputs $S0$, $S1$, … . The state inputs address which of the data input is routed to the data output. An example is given in Abbildung 38. When $S0 = 0$ and $S1 = 0$ the zeroth data input $D0$ is the output, for $S0 = 1$ and $S0 = 0$ the first data input $D1$, for $S0 = 0$ and $S0 = 1$ the second. The 'inner life' of the multiplexer will be shown in chapter 3.
A demultiplexer is the counterpart to the multiplexer: It has one data input $D$ and several data outputs $Y0$, $Y1$, … . Again there are also state inputs $S0$, $S1$ … . Here, the state inputs address to which data output the single data input is routed. Also, this is shown in Abbildung 38.
With the background given in subchapter 1.6.3, the demultiplexer can be derived. In the example, in subchapter 1.6.3 an input was forwarded to 2 outputs. We will now have a look at a demultiplexer with 4 outputs. For this instead of an AND gate with two inputs an AND gate with three inputs is used. The topmost input is the data input $D$ for all gates. The other two inputs address which of the AND gate will route the data input. When one has a detailed look at the addressing inputs, one can see at any time that only one AND gate has both lower inputs high.
related Links
- Solver for Boolean functions: The solver specifies with which axioms Boolean equations can be simplified.
- Wolfram Alpha shows the different representations for boolean statements
- A nice overview of core ideas for calculating with electricity has been compiled by Gymnasium Kirchenfeld (CH, in German)
- Explanation of CMOS in the English Wikipedia
- Wiki page on integrated circuits
- Silicon Zoo: Here you can see the practical implementation of logic gates in silicon.
Applications
- Etherium: With this cryptocurrency, calculations on the blockchain are possible. Here, the basic logical functions are the most convenient - so a program should be feasible with as few boolean operators as possible
- Example in C for using of boolean algebra: by clicking on the Fork this button, the code can be changed.
Exercises
Exercise 1.6.2. truth tables
Exercise 1.6.3. timing diagram
Exercise 1.6.4. NAND-based gates
Realize the logic functions of NOT, AND, OR, NOR, XOR, and XNOR exclusively with NAND gates.
An inverter can be realized with a NAND gate when both inputs are connected to the same input.
When the input is $1$ the output will be $0$ and vice versa.
AND
With the realization of the NOT gate an AND gate is also simple: just put the NOT after a NAND.
OR
With the realization of the NOT gate an AND gate is also simple: just put the NOT after a NAND.
NOR
Again the NOR gate can be derived from the NOT gate and OR gate.
XOR
The XOR gate is a bit more complex. One path to a solution is the following:
- The XOR-gate only outputs a $0$ in the two cases $(X0=0, X1=0)$, $(X0=1, X1=1)$.
- Therefore, as a first idea, it would be great to have gates detecting $X0=0\; and\; X1=0$ such as $X0=1\; and\; X1=1$.
- The ladder one is $X0\cdot X1$, which is only $1$ for both inputs as $1$.
- For detecting $X0=0\; and\; X1=0$ one can use $\overline{X0+X1}$, which is only $1$ for both inputs are $0$.
- These two gates have to be combined in such a way that, only for $(X0=0, X1=0)$, $(X0=1, X1=1)$ the final output is $1$.
In other words: only when the output of the AND- and the NOR-gates is $0$, the final output has to be $1$. \\For this, a NOR gate can be used. - All of the mentioned gates can be built based on NAND gates. This is shown in Abbildung 46.
The shown circuit can even be simplified:
- Two Not-gates in series can be skipped since $\overline{\overline{X}}=X$.
With this knowledge, the XOR-gate needs 6 NAND gates. - An alternative setup for the XOR-gate can be built by one NAND-, one OR-, and one AND-gate. This circuitry needs also 6 NAND gates. \\The circuitry is not shown.
- The circuity with the least NAND gates is shown in Abbildung 47
Exercise 1.6.5. NOR-based gates
Realize the logic functions of NOT, OR, AND, NAND, XOR, and XNOR exclusively with NOR gates.
Exercise 1.6.6. simplification of logic expressions
Simplify the following expressions with boolean algebra. Write down the rule for each step!
- $Y = (/X0*/X1*/X2) $$+ (X0*X1*/X2) $$+ (/X0*/X1*X2) $$+ (X0*X1*X2)$
- $Y = (X0*X1*X2*X3) $$+ (X0*X1*X2*/X3) $$ + (X0*X1*/X2*/X3) $$+ (/X0*X1*X2*X3)$
- $Y = (X0*X1*X2*X3) $$+(/X0*X1*X2*X3) $$+ (/X0*X1*/X2*X3)$
- $Y = (/X0*X1*/X2*/X3) $$+ (/X0*X1*X2*X3) $$+ (X0*/X1*/X2*X3) $$+ (/X0*/X1*/X2*/X3)$
- $Y = (/X0*/X1*/X2*/X3) $$+ (/X0*X1*/X2*/X3) $$+ (/X0*/X1*/X2*X3) $$+ (/X0*X1*/X2*X3)$
Additionally, the brackets can be ignored in the case of products - similar to the convention in math for $(a \cdot b) + (c \cdot d) = ab + cd$
$Y = \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\;\color{red}{\overline{X_2}}$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{red}{\overline{X_2}}$$ + \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\;\color{salmon}{ {X_2}}$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}$
With the commutative law switching term 2 and term 3 is possible:
$Y = \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\;\color{red}{\overline{X_2}} $$ + \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\;\color{salmon}{ {X_2}}$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{red}{\overline{X_2}} $$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}
$
Based on the distributive law the parts $\color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}$ and $\color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}$ can be placed outside the brackets:
$Y = \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\;(\color{red}{\overline{X_2}} + \color{salmon}{ {X_2}})$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;(\color{red}{\overline{X_2}} + \color{salmon}{ {X_2}})$
The rule of the complementary element tells us that $a +\overline{a} = 1$ and based on the neutral element $a\cdot 1 = a$:
$Y = \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}\cdot 1$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\cdot 1$
÷
$Y = \color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}}$$ + \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}
$
At this point, there is no other law available. But when we look onto the last formula $Y$ is only $1$ when either $\color{blue}{\overline{X_0}}\;\color{green}{\overline{X_1}} = 1$ or $\color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}} = 1$.
Therefore, $Y$ is only $1$ in two cases:
- $\color{cornflowerblue}{X_0 }=0$ and $\;\color{yellowgreen}{ {X_1}} = 0$ or
- $\color{cornflowerblue}{X_0 }=1$ and $\;\color{yellowgreen}{ {X_1}} = 1$
This is the definition of the $XNOR$. So the final step would be:
$Y = \overline{\color{cornflowerblue}{X_0} \text{#} \color{yellowgreen}{X_1} }$
Additionally, the brackets can be ignored in the case of products - similar to the convention in math for $(a \cdot b) + (c \cdot d) = ab + cd$ \begin{align*} Y &= \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{red}{\overline{X_2}}\;\color{brown}{\overline{X_3}}\\ \end{align*}
With the idempotence the term 2 can be doubled: \begin{align*} Y &= \color{cornflowerblue}{X_0 }\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{red}{\overline{X_2}}\;\color{brown}{\overline{X_3}}\\ \end{align*}
The commutative law enables to rearrange within the terms: \begin{align*} Y &= \color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}}\;\color{cornflowerblue}{X_0 } + \color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}}\;\color{blue}{\overline{X_0}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;\color{salmon}{ {X_2}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;\color{red}{\overline{X_2}}\\ \end{align*}
Based on the distributive law the parts $\color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_2}}$ and $\color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_2}}$ to place outside the brackets:
\begin{align*} Y &= \color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}}\;(\color{cornflowerblue}{X_0 } + \color{blue}{\overline{X_0}}) + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;(\color{salmon}{ {X_2}} + \color{red}{\overline{X_2}})\\ \end{align*}
The rule of the complementary element tells us that $a +\overline{a} = 1$ and based on the neutral element $a\cdot 1 = a$:
\begin{align*} Y &= \color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}}\cdot 1 + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\cdot 1\\ \\ Y &= \color{yellowgreen}{ {X_1}}\;\color{salmon}{ {X_2}}\;\color{brown}{\overline{X_3}} + \color{blue}{\overline{X_0}}\;\color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\\ \end{align*}
Again, the commutative law can be used: \begin{align*} Y = \color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;\color{salmon}{ {X_2}} + \color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;\color{blue}{\overline{X_0}}\\ \end{align*}
And the distributive law: \begin{align*} Y = \color{yellowgreen}{ {X_1}}\;\color{brown}{\overline{X_3}}\;(\color{salmon}{ {X_2}} + \color{blue}{\overline{X_0}})\\ \end{align*}
Exercise 1.6.7. only using NAND
Rewrite the following expressions using only NAND. Check the result for equality using truth tables.
- $Y = X0 + X1*/X2$
- $Y = /(/X0*X1)$
- $Y = X0*X1 + /X2$
- $Y = /X0*/X1$
- $Y = /(/(X0+X1) + X0*X1)$
- $Y = /(/X0+X1+/X2) + /(X0+/X1+X2)$
Generally, the first step would be to see which of the parts show already a NAND configuration. In the following, these are marked in $\color{magenta}{magenta}$.
In this case, there are no terms with NAND available.
One of the next steps is to do substitutions with the DeMorgans rule: $\overline{a+b}=\overline{a}\cdot\overline{b}$.
This can be used on the outer negation:
\begin{align*} Y = \overline{\overline{X0+X1}} \cdot \color{magenta}{\overline{X0 \cdot X1}} \end{align*}
This can be done again on $\overline{X0+X1}$:
\begin{align*} Y = \color{magenta}{\overline{\color{black}{\overline{X0}}\cdot \color{black}{\overline{X1}}}} \cdot \color{magenta}{\overline{X0 \cdot X1}} \end{align*}
The last step is the substitution of the inverted parts: $\overline{X}=\color{magenta}{\overline{X\cdot X}}$
\begin{align*} Y = \color{magenta}{\overline{\overline{X0 \cdot X0}\cdot \overline{X1 \cdot X1}}} \cdot \color{magenta}{\overline{X0 \cdot X1}} \end{align*}
Exercise 1.6.8. step-by-step example for logic simplification using boolean rules
Hints for the clip:
- The ladder logic is not necessary for our course.
- Example 1 is quite exhausting including a recap of the boolean rules $\rightarrow$ you can skip this example
- Example 2 starts at 17:17
- Example 3 starts at 21:00
- Example 4 starts at 28:27
- Examples 5-8 start at 32:33
Exercise 1.6.9. XOR in Cryptography
In the following EXCEL file, an example of symmetric encryption can be found: xor_in_cryptography.xlsx
- Try to understand XOR_cipher with this example.
- Which advantages and disadvantages does symmetric encryption have?
References
- Abbildung ##: David Carron@Wikimedia,public domain