4 Realization of Combinatorial Logic
4.1 Preparation
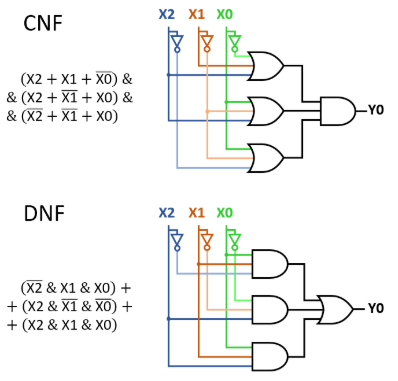
In the last chapter, we investigated the Therm-o-Safety example. From this, it was possible to create the logic formula via sum-of-products of product-of-sums (see Abbildung 1).
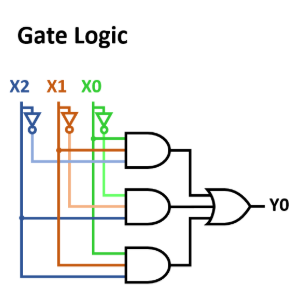
It is simple to derive the gate logic from the formula (Abbildung 2). For each of the three (min)terms, an AND-gate combines the needed inputs. As shown in the image, the inverted inputs are usually drawn parallel to the inputs.
The main question is now: which generalization of the shown logic can be found?
4.1.1 History of the Logic Families
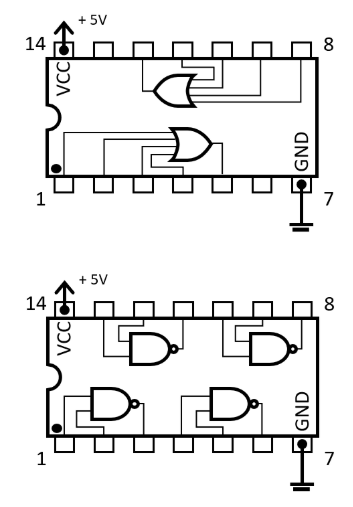
A huge variety of integrated circuits (ICs) were used historically. Abbildung 3 shows two separate integrated circuits: There can be single or multiple gates in an IC with two or more inputs. The most used IC series was the 74xx ICs, where the xx are numbers that define the internal logic.
The logic families which were first developed were based on bipolar transistors. To use these as a closed switch a constant current is needed. This results in relatively high power losses. Depending on the combination of these transistors these logic families were called „transistor-transistor logic“ (TTL) or „emitter-coupled logic“ (ECL). The name TTL survived as a designation for the needed voltage levels $0V$ and $5V$. The $5V$ can still be found as supply voltage in some logic circuits.
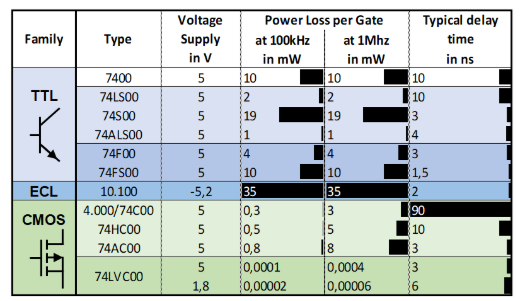
Modern controller logic is based on CMOS. Abbildung 4 shows that this type of logic only dissipates a fraction of the energy loss (and therefore heat) compared to the older logic families. This started the logic circuit development, which led to mobile phones, computers, and all the other present digital controllers.
The 74xx series is nowadays mostly from historical interest. Nearly all of the applications can now be done directly with microcontrollers. In rare cases, they are still used as „glue logic“ between two logic ICs, e.g. for adjusting the logic voltage level.
4.1.2 Logic Stages
From the Abbildung 2 we know what the logic for the sum-of-products looks like. in Abbildung 5 also the gate logic for the product-of-sums is shown. Both consist of two logic stages:
- For sum-of-products the first logic stage is set up with OR-gates, the second stage is the AND-gate,
- For product-of-sums, it is just the other way around: first logic stage AND-gates, second stage OR-gate.
Generally, the two-stage setup allows the implementation of any possible logic based on a truth table.
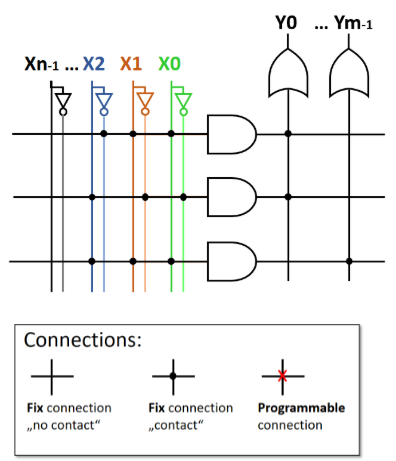
Often a simplification of the circuit representation is used. There the multiple input and output lines are reduced to one single line, representing a bus (= multiple parallel lines). Only the inputs where the crossing of the lines is marked with a black dot are used as input for the stages. These connections are fixed. Often also programmable connections are used, which are usually set during production. The logic stages can be seen in Abbildung 6.
4.2 Programmable Logic Device
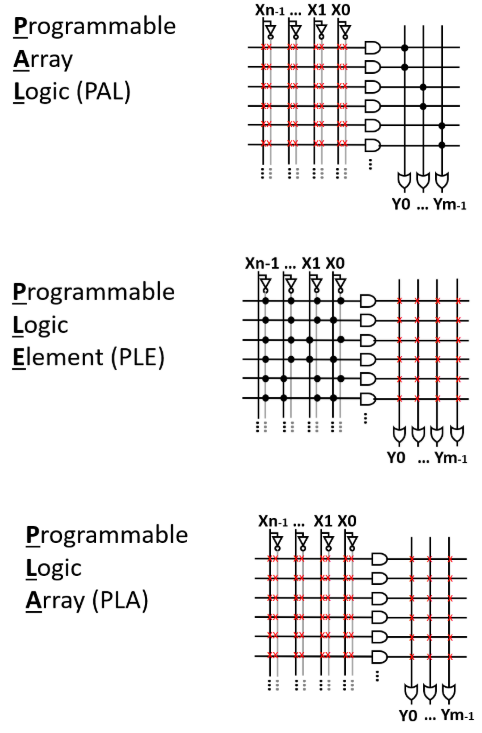
When there are programmable connections, the IC is called a programmable logic device (PLD). Depending on the position of the programmable connections, these PLDs are separated into (see Abbildung 7):
- Programmable Array Logic (PAL): the first stage is programmable, the second stage is fixed
- Programmable Logic Element (PLE): the first stage is fixed, the second stage is programmable
- Programmable Logic Array (PLA): both stages are programmable
4.2.1 Programmable Logic Elements
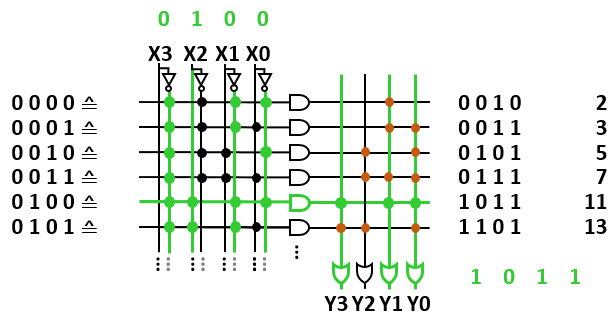
PLEs have fixed AND array logic in stage 1. This is often used in memory chips.
The AND array logic for memory chips represents a list of increasing digital values (see the left stage in Abbildung 8).
In the picture, the first 6 prime numbers are stored in a 4-bit addressed 4-bit memory.
The input value 0100 activates only one AND-gate, which enables one column of the OR array logic to be output.
In Abbildung 9 the simulation shows a PLE. In the top left corner, the address is shown in decimal. The logic enables only the address 0 up to 8 to have an output. The address increases and therefore step by step the information - given by the right-side array - is read. In the bottom right corner, the memory of the address is shown in decimal. By clicking on the switches on the right side, in the second stage, one can also reprogram the stored information.
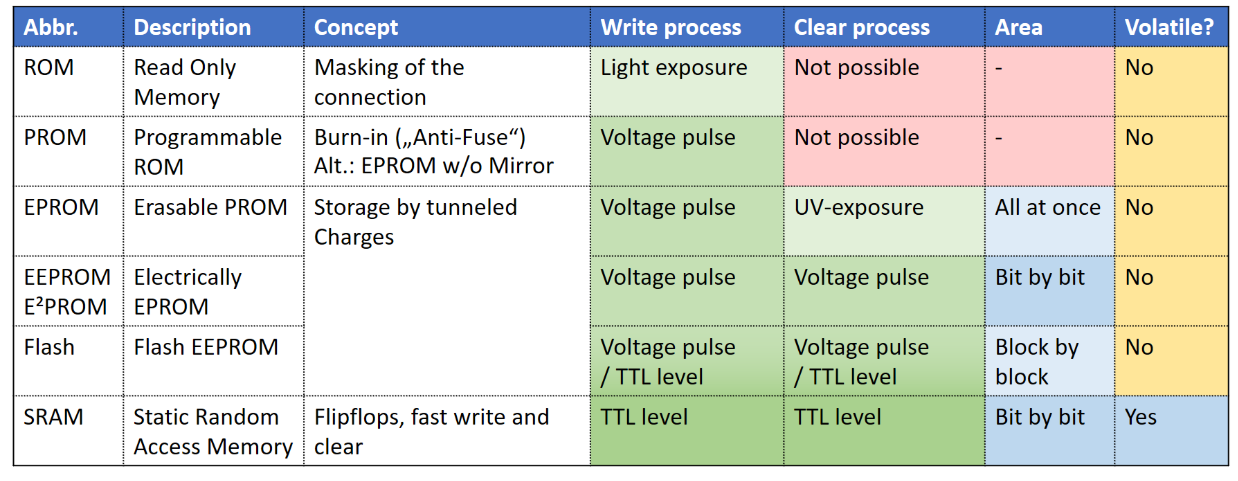
There are different types of memory available. The Abbildung 10 shows an overview separated by the different physical concepts of writing and clearing the information.
A good practical example for an application is key cards or canteen cards (like your mensa card). There a small Operating system is stored in a ROM. They also use a one-time programmable (OTP) PROM to secure the internal cryptographic secret. In a Flash ROM, the user can write additional reprogrammable data.
4.2.2 Programmable Logic Arrays and Programmable Logic Elements
PLA was often used as glue logic but is nowadays rarely in use. Abbildung 11 shows the principal setup. Based on PLAs - and especially on PLEs - more complex logic devices are developed.
Nowadays High Capacity Programmable Logic Devices are in use:
- These are either Complex Programmable Logic Devices (CPLD), which have multiple sum-of-products or products-of-sum stages, with small storages in between.
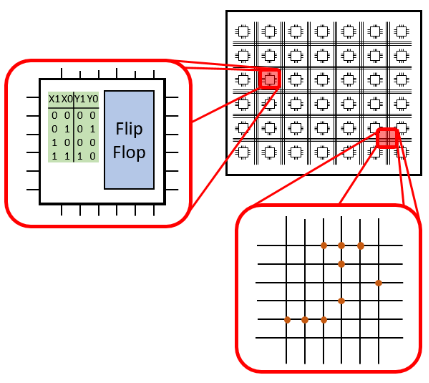
- There are also Field-Programmable Gate Arrays (FPGA). These have a huge number (>100'000) of simple functional blocks. One functional block contains the logic gate circuit and storage elements. Between the blocks are broad binary busses. The logic circuits, storage elements, and bus allocation can be changed by reconfiguration. In Abbildung 12 the logic gate circuit is represented by a truth table. The storage element called flipflop will be investigated in the next chapter.
FPGAs can be used to test new microcontrollers and microchips. For this, the FPGA is configured in such a way, that it resembles the new chip.
A deeper explanation of the FPGA can be found here: