Aufgabe 3.1.3: Last an linearer Quelle (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
Gegeben ist eine lineare Stromquelle, welche eine ohmsche Last $R_L=10\Omega$ versorgt. Es ergibt sich ein Strom an der Last von $I_L=2A$. Der Kurzschlussstrom ist $5 A$.
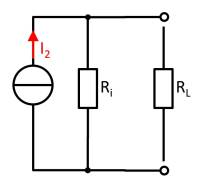
1. Zeichnen Sie das Ersatzschaltbild des Aufbaus.
- Wie Sieht eine lineare Stromquelle aus?
- Wie wird die Last verschalten?
2. Wie groß die der Innenleitwert der Quelle?
- Im Kurzschlussfall fließt der Kurzschlussstrom nur durch $R_L$
- Für eine Vereinfachung der Rechnung bietet es sich an die lineare Stromquelle in eine lineare Spannungsquelle umzuwandeln.
Die Umwandlung der lineare Stromquelle in eine lineare Spannungsquelle ergibt eine Leerlaufspannung $U_{LL}=R_i \cdot I_{KS}$.
Die Umwandlung wandelt auch die Schaltung von einer Parallelschaltung in eine Reihenschaltung.
Die Spannung $U_{LL}$ liegt also am Spannungsteiler aus $R_i$ und $R_L$: $U_{LL} = U_i + U_L$
Mit dem Lastwiderstand $R_L$ ergibt sich ein Strom von $I_L$ durch die Reihenschaltung.
Mit den gegebenen $R_L$ und $I_L$ lässt sich die Spannung $U_L$ an der Last berechnen.
Die restliche Spannung $U_i$ liegt am Innenwiderstand $R_i$ an, durch den auch der Strom $I_L$ fließt. Somit ergibt sich für den Leitwert $G_i$:
Die Umwandlung wandelt auch die Schaltung von einer Parallelschaltung in eine Reihenschaltung.
Die Spannung $U_{LL}$ liegt also am Spannungsteiler aus $R_i$ und $R_L$: $U_{LL} = U_i + U_L$
Mit dem Lastwiderstand $R_L$ ergibt sich ein Strom von $I_L$ durch die Reihenschaltung.
Mit den gegebenen $R_L$ und $I_L$ lässt sich die Spannung $U_L$ an der Last berechnen.
Die restliche Spannung $U_i$ liegt am Innenwiderstand $R_i$ an, durch den auch der Strom $I_L$ fließt. Somit ergibt sich für den Leitwert $G_i$:
\begin{align*} U_{LL} &= U_i + U_L \\ R_i \cdot I_{KS} &= R_i \cdot I_L + R_L \cdot I_L \\ R_i \cdot I_{KS} - R_i \cdot I_L &= R_L \cdot I_L \\ R_i \cdot (I_{KS} - I_L) &= R_L \cdot I_L \\ R_i &= R_L \cdot \frac{I_L}{I_{KS} - I_L} \\ G_i &= \frac{I_{KS} - I_L}{R_L \cdot I_L} \\ \end{align*}
\begin{align*}
G_i &= \frac{5A - 2A}{10 \Omega \cdot 2A} = 0,15 S \\
\end{align*}
3. Welche Leistung nimmt die Last auf?
\begin{align*}
P = R_L \cdot I_L^2 = 10 \Omega \cdot (2A)^2 = 40 W \\
\end{align*}