Dies ist eine alte Version des Dokuments!

6. Filterschaltungen II - Filter höherer Ordnung

6.1 Bandpassfilter

Abb. 1: Beispiel: WLAN-Kanäle
elektronische_schaltungstechnik:wlan_kanaele.png

Bei der Analyse unterschiedlicher Signale ist nur ein Teil des gesamten Frequenzspektrums gewünscht. In Abbildung 1 sind als Beispiel die Kanäle des WLAN Standards 802.11 dargestellt; Diese werden abwechselnd zur Datenübertragung genutzt. Ein weiteres Beispiel ergibt sich bei Schwingungsspektren eines Motors in einer Maschine, welche nicht nur die (zur Diagnose verwendbaren) Schwingungen enthält, sondern auch Störungen durch andere Maschinenteile. Andere Beispiele ist die kabelgebundene Datenübertragung oder die Bänder der Gehirnwellen.

Zur Separierung der gewünschten Frequenzen kann ein Filter genutzt werden, welcher nur ein vorgegebenes Band zwischen zwei Frequenzen (Frequenzband) durchlässt. Dies ist mit einem Bandpassfilter möglich.

Abb. 2: Toleranzschema für ein Bandpassfilter
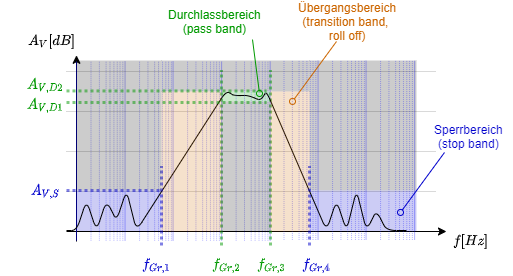
elektronische_schaltungstechnik:toleranzschema_bandpassfilter.png

Bereiche im Frequenzgang

Den Bereich zwischen den zwei Frequenzen nennt man Durchlassbereich, oder Bandbreite. Außerhalb des Durchlassbereichs fällt die Verstärkung ab. Ein reelles Filter kann nicht unendlich stark abschwächen. Auch gibt es verschiedene ideale Filtern, bei denen außerhalb des Durchlassbereichs nicht Verstärkung nicht gegen Null strebt, sondern nur ein Schwelle unterschreitet. Häufig wird der der abfallende Bereich Übergangsbereich genannt und der der Bereich unterhalb der Schwelle Sperrbereich. Die Schwelle selbst nennt man Sperrdämpfung. In Abbildung 2 sind die Bereiche eingezeichnet. Die Begriffe sind aber nicht eindeutig definiert; in verschiedenen Lehrbüchern wird bereits der Übergangsbereich als Sperrbereich bezeichnet.

Abb. 3: Blockschaltbild Bandpass
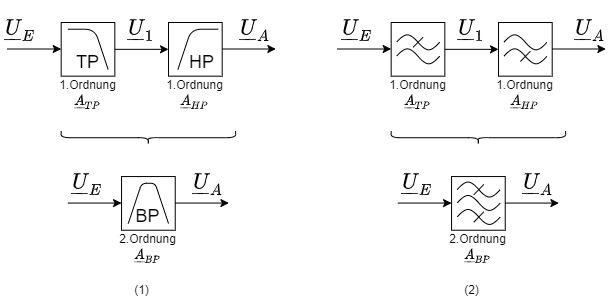
elektronische_schaltungstechnik:blockschaltbild_bandpass.png

Zusammensetzen des Bandpass Filter

Dieses Filter lässt sich über durch grundlegenden Tief- und Hochpassfilter zusammensetzen. Wird zunächst der Signal durch einen Tiefpass und anschließend durch einen Hochpass gefiltert, so entsteht das gewünschte Filter. Die Reihenfolge der Filter kann vertauscht werden. Abbildung 3 zeigt dies im Blockschaltbild - dabei ist in (1) ein häufig genutzte und in (2) mit den nach EN 60617 zu verwendenden Schaltzeichen. Damit ergibt sich die Übertragungsfunktion $\underline{A}_{BP}$ des Bandpasses einfach aus der Übertragungsfunktion der Tief- und Hochpassfilter $\underline{A}_{TP}$ und $\underline{A}_{HP}$, da das Signal nacheinander durch die Filterstufen läuft:

$$\underline{A}_{BP}= {{\underline{U}_A}\over{\underline{U}_E}} = {{\underline{U}_A}\over{\underline{U}_1}} \cdot {{\underline{U}_1}\over{\underline{U}_E}} = \underline{A}_{TP} \cdot \underline{A}_{HP}$$

Abb. 4: Amplitudengang Bandpass
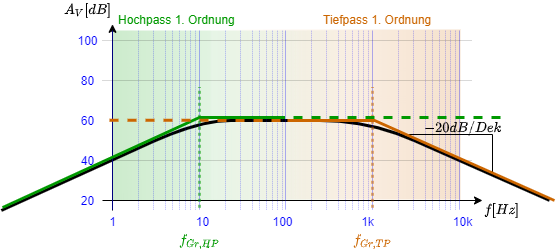
elektronische_schaltungstechnik:amplitudengang_bandpass.png

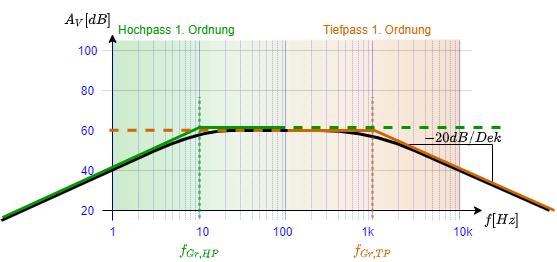
Amplitudengang des Bandpass Filter

In Abbildung 4 ist der Amplitudengang des Bandpassfilter zu sehen. Da im Amplitudengang die Übertragungsfunktion in $dB$ ($\underline{A}^{dB}$) dargestellt wird, ergibt sich aus der Multiplikation der Übertragungsfunktion der Tief- und Hochpassfilter $\underline{A}_{TP}$ und $\underline{A}_{HP}$ eine Addition von $\underline{A}_{TP}^{dB}$ und $\underline{A}_{HP}^{dB}$. Im Amplitudengang ist zu sehen, dass es zweimal eine Änderung um $20 dB/Dek$ ergibt: einmal bei $f_{Gr,HP}$ und einmal bei $f_{Gr,TP}$. Das Filter hat also eine Ordnung von 2.

Wichtig dabei: Die Grenzfrequenz des Tiefpassfiter $f_{Gr,TP}$ muss größer sein, als die Grenzfrequenz des Hochpassfilter $f_{Gr,HP}$ (siehe Abbildung 4).

Wie sieht aber nun der Frequenzgang aus? Dies soll im Folgenden hergeleitet werden.

Abb. 5: Schaltung des Bandpassfilter auf Basis des invertierenden Verstärkers
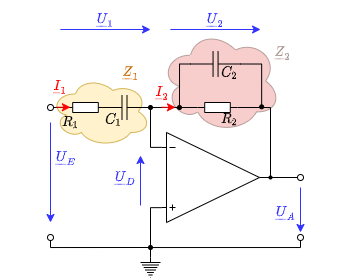
elektronische_schaltungstechnik:schaltung_bandpassfilter_invertierender_verstaerker.png

Bandpass auf Basis des invertierenden Verstärkers

Realisation

Aus Kapitel 5 sind die Schaltungen von Hochpass- und Tiefpass-Filter bekannt. Daraus lässt sich die in Abbildung 5 dargestellte Schaltung ableiten. Diese soll etwas näher betrachtet werden.

Die Extremalwertbetrachtung ergibt:

  • für $ \omega \rightarrow 0 $:
    Der Betrag der Impedanz der Kapazitäten wird groß
    und damit ist $|\underline{X}_{C_1}| \gg R_1$ , sowie $|\underline{X}_{C_2}| \gg R_2$
    Es überwiegt also $\underline{X}_{C_1}$ bei $\underline{Z}_1$ und $\underline{R}_2$ bei $\underline{Z}_2$.
    $\rightarrow$ Bei tiefen Frequenzen ergibt sich ein Umkehr-Differentiator.
  • für $ \omega \rightarrow \infty $:
    Der Betrag der Impedanz der Kapazitäten wird klein
    und damit ist $|\underline{X}_{C_1}| \ll R_1$ , sowie $|\underline{X}_{C_2}| \ll R_2$
    Es überwiegt also $\underline{R}_1$ bei $\underline{Z}_1$ und $\underline{X}_{C_2}$ bei $\underline{Z}_2$.
    $\rightarrow$ Bei hohen Frequenzen ergibt sich ein Umkehr-Integrator.


komplexwertige Betrachtung der Übertragungsfunktion

Die Übertragungsfunktion soll wieder aus einem komplexwertigen, invertierenden Verstärker hergeleitet werden:

$\underline{A}_V = {{\underline{U}_A}\over{\underline{U}_E}} = - {{\underline{Z}_2}\over{\underline{Z}_1}} = - {\underline{Z}_2}\cdot {1\over{\underline{Z}_1}} = - \Large{{{R_2\cdot {1\over{j\omega C_2}}}\over{{R_2 + {1\over{j\omega C_2}}}}}}\cdot{1 \over{{R_1 + {1\over{j\omega C_1}}}}}= - \Large{{{R_2}\over{{j\omega C_2 R_2 + 1}}}}\cdot{j\omega C_1 \over{{j\omega C_1 R_1 + 1}}} \Bigg| {{\cdot R_1}\over{\cdot R_1}}$

$\boxed{\underline{A}_V = - \color{blue}{R_2 \over R_1 } \cdot \large\color{teal}{1 \over {1+ j\omega \cdot C_2 R_2}} \cdot \large\color{brown}{{j\omega \cdot C_1 R_1} \over {1+ j\omega \cdot C_1 R_1}}}$

Durch die geschickte Umformung ergibt sich ein interessantes Ergebnis aus folgenden Teilen:

  1. $- \color{blue}{R_2 \over R_1 }$: Dies entspricht dem invertierenden Verstärker
  2. $\large\color{teal}{1 \over {1+ j\omega \cdot C_2 R_2}}$: Dies entspricht dem Tiefpass 1. Ordnung
  3. $\large\color{brown}{{j\omega \cdot C_1 R_1} \over {1+ j\omega \cdot C_1 R_1}}$: Dies entspricht dem Hochpass 1. Ordnung


Damit ergibt sich über die Extremalwertbetrachtung als Funktion:

  • für $ \omega \rightarrow 0 $:
    $\underline{A}_V = - \Large{R_2 \over R_1 } \cdot \Large\color{teal}{1 \over {1+ \color{black}{\underbrace{\color{teal}{j\omega \cdot C_2 R_2}}_{\rightarrow 0}}}} \cdot \Large\color{brown}{{j\omega \cdot C_1 R_1} \over {1+ \color{black}{\underbrace{\color{brown}{j\omega \cdot C_1 R_1}}_{\rightarrow 0}}}} \rightarrow - {R_2 \over R_1 } \cdot \color{teal}{ 1 \over 1} \cdot \Large\color{brown}{{j\omega \cdot C_1 R_1} \over 1} \rightarrow - \color{brown}{\normalsize{j\omega \cdot C_1 \color{black}{R_2}}}$
    Die Gleichung entspricht der eines Umkehr-Differentiators

  • für $ \omega \rightarrow \infty $:
    $\underline{A}_V = - \Large{R_2 \over R_1 } \cdot \Large\color{teal}{1 \over {1+ j\omega \cdot C_2 R_2}} \cdot \Large\color{brown}{{j\omega \cdot C_1 R_1} \over \color{brown}{1+ {j\omega \cdot C_1 R_1}}} \rightarrow - {R_2 \over R_1 } \cdot \color{teal}{ 1 \over {j\omega \cdot C_2 R_2}} \cdot \Large\color{brown}{1 \over 1} \rightarrow - \color{teal}{1 \over {j\omega \cdot C_2 \color{black}{R_1}}}$
    Die Gleichung entspricht der eines Umkehr-Integrators


Ermittlung von Betrag und Phase aus der komplexwertigen Betrachtung

Für den Betrag $|\underline{A}_V|$ der Übertragungsfunktion kann folgender Tipp genutzt werden: $|a\cdot b\cdot c| = |a| \cdot |b| \cdot |c| $.
Damit ergibt sich für den Betrag $|\underline{A}_V|$:
$|\underline{A}_V| = {R_2 \over R_1 } \cdot \large{1 \over \sqrt{1+ \omega^2 C_2^2 R_2^2}} \cdot \large{{\omega \cdot C_1 R_1} \over \sqrt{1+ \omega^2 C_1^2 R_1^2}}$

Für die Phase $\varphi$ muss wieder konjungiert komplex erweitert werden.
Dies erzeugt zwar zunächst eine unhandliche Gleichung - aus dieser kann aber eine realwertige Konstante abgetrennt werden.

$\underline{A}_V = - \color{blue}\large{R_2 \over R_1 } $ $\cdot \large\color{teal }{ 1 \over \color{lightgray}{\boxed{\color{teal }{\small{1+ j\omega \cdot C_2 R_2}}}}}$ $\cdot \large\color{teal }{{1- j\omega \cdot C_2 R_2} \over \color{lightgray}{\boxed{\color{teal }{\small{1- j\omega \cdot C_2 R_2}}}}}$ $\cdot \large\color{brown}{{ j\omega \cdot C_1 R_1} \over \color{ pink }{\boxed{\color{brown}{\small{1+ j\omega \cdot C_1 R_1}}}}}$ $\cdot \large\color{brown}{{1- j\omega \cdot C_1 R_1} \over \color{ pink }{\boxed{\color{brown}{\small{1- j\omega \cdot C_1 R_1}}}}}$

$\underline{A}_V = \quad \quad \quad \mathcal{C} \quad \quad \quad \quad$ $ \cdot \color{teal }{(1- j\omega \cdot C_2 R_2)}$ $\ \cdot \ \color{brown}{ j\omega \cdot C_1 R_1 }$ $\ \cdot \ \color{brown}{(1- j\omega \cdot C_1 R_1)}$

$\underline{A}_V = \quad \quad \quad \mathcal{C} \quad \quad \quad \quad$ $ \cdot (j + \omega R_2 C_2 + \omega R_1 C_1 - j \omega R_1 C_1 \omega R_2 C_2)$

Aus dieser Gleichung lassen sich einfach die Anteile für Realteil $\Re(\underline{A}_V)$ und Imaginärteil $\Im(\underline{A}_V)$ ablesen.
Damit ergibt sich für die Phase $\varphi$ :

$\varphi = arctan \left( \frac{\Im(\underline{A}_V)}{\Re(\underline{A}_V)} \right) = arctan \left( \frac{1 - \omega R_1 C_1 \omega R_2 C_2}{\omega R_2 C_2 + \omega R_1 C_1} \right)$

und mit den Grenzfrequenzen $\color{teal}{\omega_{Gr, TP} = {1 \over {R_2 C_2}}}$ und $\color{brown}{\omega_{Gr, HP} = {1 \over {R_1 C_1}}}$

$\varphi = arctan \left( \Large\frac{\color{teal}{\omega_{Gr, TP}} \color{brown}{\omega_{Gr, HP}} - \omega^2 }{\omega (\color{teal}{\omega_{Gr, TP}}+\color{brown}{\omega_{Gr, HP}})} \right)$


Die Formal für für die Phase $\varphi$ sagt Die Extremalwertbetrachtung kann nun für einige markante Frequenzen geführt werden:

  • für $ \omega \rightarrow 0 $:
    $\varphi(0) = arctan \left( \frac{\mathcal{C}_1 - \omega^2}{\omega \mathcal{C}_2} \right) \rightarrow arctan \left( \frac{\mathcal{C}_1 - "0"}{"0"} \right) = arctan \left( "+\infty" \right)$

  • für $ \omega \rightarrow \infty $:
    $\varphi(\infty) = arctan \left( \frac{\mathcal{C}_1 - \omega^2}{\omega \mathcal{C}_2} \right) \rightarrow arctan \left( \frac{\mathcal{C}_1 - "\infty"^2}{"\infty"} \right) = arctan \left( "-\infty" \right)$

  • für eine (Kreis)Frequenz $\omega= \omega_0$ für die das Argument der $arctan$-Funktion Null wird:
    \frac{\color{teal}{\omega_{Gr, TP}} \color{brown}{\omega_{Gr, HP}} - \omega^2 }{\omega (\color{teal}{\omega_{Gr, TP}}+\color{brown}{\omega_{Gr, HP}})} = 0 \rightarrow \omega_0^2 = \color{teal}{\omega_{Gr, TP}} \color{brown}{\omega_{Gr, HP}} \rightarrow \omega_0 = \sqrt{1 \over \color{teal}{\omega_{Gr, TP}} \color{brown}{\omega_{Gr, HP}}}$: \\ $\varphi(\omega_0) = arctan \left( 0 \right)$

  • für die Grenzfrequenz des Hochpassfilter $\color{brown}{\omega=\omega_{Gr, HP} = {1 \over {R_1 C_1}}}$: Hierfür kann bei hinreichend großem Durchlassbereich $\color{brown}\omega_{Gr, HP} \ll \color{teal}\omega_{Gr, TP}$ angenommen werden. Damit ergibt sich:
  • häufig ist der Durchlassbereich Durchlass, dass $\omega_{Gr, HP}

Abb. 8: Bodediagramm Bandpass
elektronische_schaltungstechnik:bodediagramm_bandpass.png

6.2 Bandsperre

Elektrotechnik 2 und Elektrotechnik Labor haben bereits Einblicke in Schwingkreise gegeben. In diesen Schaltungen ergeben sich bei bestimmte Frequenzen Schwingungen, die Energien aus dem System aufnehmen können

Von der Seite www.geogebra.org/m/zhvkeaa8, Autor: Tim Fischer.

Hausarbeiten

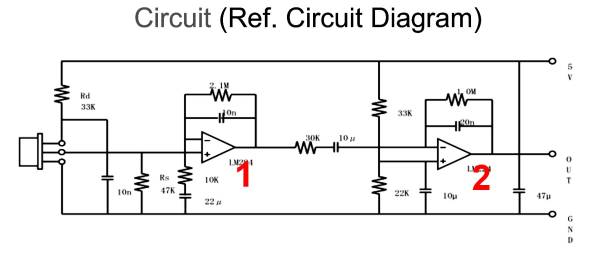
Beispiel: Auswertung eines Infrarot-Sensors:

  • Vom Hersteller fehlen die Knoten in der Schaltung --> korrekte Schaltung ist zu zeichnen
  • welchen Grundschaltungen entspricht OPV 1 und 2? Welchen Filtenn entsprechen beide?

murata_beispiel_opv_schaltung.jpg

Referenzen

Referenzen zu den genutzten Medien
Element Lizenz Link
Abbildung ##: Überlagerung von sinusförmigen Schwingungen Public Domain https://en.wikipedia.org/wiki/File:Fourier_transform_time_and_frequency_domains.gif
Abbildung 8: Überlagerung von sinusförmigen Schwingungen CC-BY SA 3.0 https://en.wikipedia.org/wiki/File:Fourier_series_square_wave_circles_animation.gif
Abbildung 6: Überlagerung von sinusförmigen Schwingungen CC-BY SA 4.0 https://commons.wikimedia.org/wiki/File:Example_of_Fourier_Convergence.gif

<--