Aufgabe 2.7.7 Vereinfachen von Schaltungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
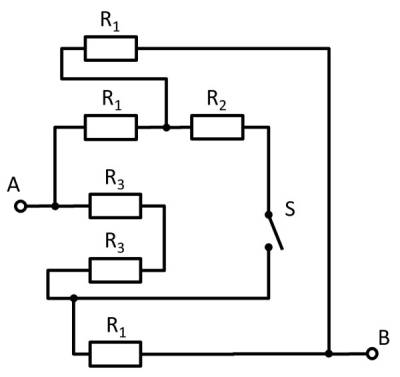
Gegeben ist die nebenstehende Schaltung mit
$R_1=10 \Omega$
$R_2=20 \Omega$
$R_3=5 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
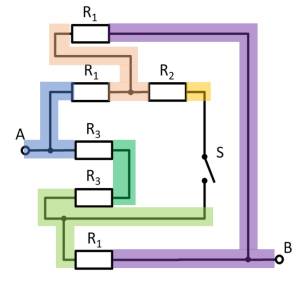
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Der Schalter sollt dabei durch eine offene Leitung ersetzt werden.
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
Es ergibt sich somit:
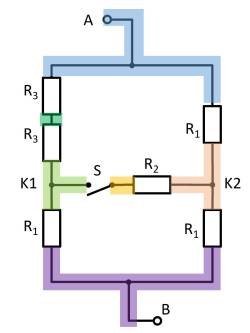
Damit lassen sich $R_3$ und $R_3$ zu $R_{33} = 2 \cdot R_3 = R_1$ zusammenfassen und es ergibt sich so ein linker und ein rechter Spannungsteiler.
Nun ist sichtbar, dass sich im linken und rechten Spannungsteiler das gleiche Potential am jeweiligen Abzweig, bzw. am Knoten K1 (grün) und K2 (pink).
Der Gesamtwiderstand lässt sich also berechnen als $R_{ges} = (2 \cdot R_1)||(2 \cdot R_1)$.
Durch die Symmetrie können aber auch die Knoten K1 und K2 kurzgeschlossen werden. Es gilt also auch $R_{ges} = 2 \cdot \left( R_1||R_1 \right)$.
2. Welcher Gesamtwiderstand ergibt sich, wenn Schalter $S$ geschlossen wird?
Der Widerstand bleibt also gleich.