Im Herzen eines Computers
Einführung
 Fig. 1: Ein Microcontroller oben ohne
Fig. 1: Ein Microcontroller oben ohne
Der Kern eines Computer ist der Prozessor in dem die Befehle ausgeführt werden. Diese Zentrale Prozessoreinheit (CPU) wird auch in Microcontrollern genutzt, die um uns herum in fast jedem Gerät zu finden sind: Mobiltelefone, PKWs, Bankkarten, Waschmaschinen… Häufig sind in den Geräten sogar mehrere Microcontroller verbaut.
Im Microcontroller ist neben dem befehlsausführenden Microprozessor (genauer der arithmetisch-logischen Einheit) auch weitere Peripherie wie Speicher, Taktgeneration, Analog-Digital-Wandler und vieles mehr verbaut. Dies macht ihn zum kompakten Werkzeug für viele Anwendungen. Betrachtet man den Microcontroller unter dem optischen Mikroskop, so ergibt sich nebenstehendes Bild (figure 1). Darin sind die verschiedenen Peripheriekomponenten zu sehen.
 Fig. 2: Microcontroller unter dem Mikroskop
Fig. 2: Microcontroller unter dem Mikroskop
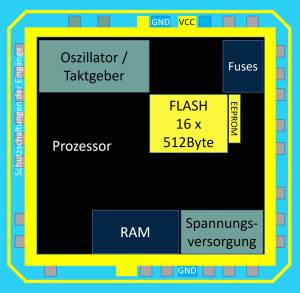 Fig. 3: Microcontroller schematisch
Fig. 3: Microcontroller schematisch
Wir wollen uns aber nun den Aufbau des Prozessors ansehen. Der in figure 2 und figure 3 dargestellte Chip wurde 1990 von zwei Studenten entwickelt und besteht aus mehreren Zehntausend Transistoren. Dieser Chip hat den Weg zu günstigen, schnellen und dennoch leicht programmierbaren Controllern, vom Faxgerät bis in den Hobbykeller, geebnet und ist u.a. auf den Arduinoboards zu finden. Den ATmega328 - einen entfernten Nachfolger mit mehreren hunderttausend Transistoren - werden Sie in höheren Semestern kennen und programmieren lernen.
Im Folgenden soll nun betrachtet werden, wie eine einfache Rechnung wie $y=a+b$ im Rechner abläuft.
zwei Transistor(typ)en reichen
Ok, nun wissen wir zumindest, dass er Chip besteht aus vielen Transistoren besteht. Aber wie funktionieren diese und wie kann man daraus so etwas komplexes wie einen Prozessor aufbauen? Die genaue Funktion ist Inhalt eines Kurses im 2. und 3. Semester. Für die digitale Anwendung ist es ausreichend ein einfaches Bild eines bestimmten Transistortyps - dem MOSFET - im Kopf zu haben. Dieser hat die drei Anschlüsse:
- Source (“Quelle”), der Zulauf der Ladungsträger
- Drain (“Senke”), der Ablauf der Ladungsträger
- Gate (“Tor”), dem Türsteher, der den Durchgang zwischen Source und Drain regelt: Liegt am Anschluss Gate die richtige Spannung1), so werden die Anschlüsse Source und Drain kurzgeschlossen, dass heißt ein Strom kann fließen und der Spannungsabfall dazwischen wird klein.
Vom MOSFET sind bei den folgenden digitalen Schaltungen zwei Typen wichtig:
- einer, der bei niedrigen Spannungen ($0V$, logisch $0$, Low, $L$ oder Falsch) am Gate nichtleitend ist (n-Kanal MOSFET) und
- einen, der bei hohen Spannungen ($5V$, logisch $1$, High, $H$ oder Wahr) am Gate nichtleitend ist (p-Kanal MOSFET).
Im Bild rechts (figure 4) sehen Sie die beiden Varianten in Aktion, wenn die Spannung am Gate gerade die digitalen Spannungswerte annimmt (vgl. Video 1 zu Zahlensysteme).
Interessant ist nun, dass diese zwei Arten von Transistoren ausreichen, um alle Varianten an logischen Funktionen aufzubauen. Logische Funktionen kombinieren einen oder mehrere Eingänge ($X_1, ... X_n$) in der Art, dass jede Art von Eingabe eindeutig zu einer Ausgabe ($Y_1, ... Y_n$) führt. In Schaltungen entsprechen sogenannte Gatter den logischen Funktionen. Dabei muss es sich nicht nur um so einfache Funktionen wie ein AND-Gatter handeln (logisches UND, Konjunktion, “nur wenn beide Eingänge wahr sind, wird der Ausgang wahr.”). Es können so auch mathematische Operationen abgebildet werden. Dazu müsstne Gatter geschickt miteinander kombiniert werden. In einer Übung zu Binärer Logik wird gezeigt, dass sich alle Gatter durch NAND- oder NOR-Gatter aufbauen lassen. Wenn wir also herausfinden könnten, wie man ein NAND oder NOR Gatter aus Transistoren aufbauen könnten, so könnte man daraus wiederum alle Gatter bis hin zur Addition aufbauen.
Gatter logisch?
Bevor das NAND-Gatter betrachtet wird, soll zunächst eine sehr einfache Schaltung aufgebaut werden, welche aus dem digitalen Eingangswert $X=0$ den Ausgangswert $Y(0)=1$ erzeugt und für $X=1$ entsprechend $Y(1)=0$. Diese Schaltung negiert also stets den Eingangswert und wird Inverter genannt. Zu diesem Zweck werden die beiden Transistortypen miteinander ähnlich eines Spannungsteilers oder einer Halbbrücke kombiniert. Damit wird immer nur ein Transistor leitfähig, der andere entsprechend hochohmig.
In figure 5 ist auch die entsprechende Schaltung mit Schließer- und Öffnerschalter gezeichnet. Wichtig für die kommende Betrachtung ist, dass die über die Schalter die logischen Spannungen ($0V$, $5V$) gerade komplementär geschalten werden. Aus diesem Grund wird diese Technik auch CMOS-Technik genannt: Complementary MOSFET. In der heutigen Elektronik ist diese Technik durchgängig in Verwendung und hat ältere Varianten (z.B. TTL) vollständig abgelöst.
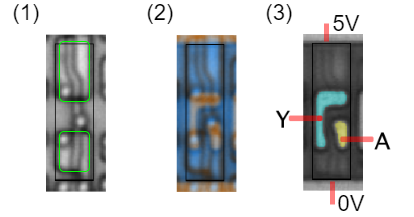
Aus diesem Beispiel ist zu sehen, wie in Mobiltelefonen, Fahrzeugsteuer- und Fernsehgeräten aus einer logischen $1$ eine $0$ werden kann. Die figure 6 zeigt die Realisierung dieses Gatters in Silizium:
- Bild (1) zeigt die Aufnahme eines Rasterelektronenmikroskop, welche mehrere Schichten gleichzeitig darstellt. Die drei kreisförmigen Elemente sind elektrische Durchlässe (“Vias”) durch mehrere Schichten. In grün sind die beiden Strukturen der MOSFETs zu sehen, welche als “Ventil” den Anschluss nach oben ($5V$) oder unten ($0V$) öffnen können.
- Bild (2) ist ein Falschfarbenbild. In beige ist die obere, leitfähige Schicht zu sehen und in blau der nicht leitfähige Bereich der oberen Schicht.
- In Bild (3) wurden die verschiedenen Signale hervorgehoben.
Der Ausgang $A$ wird über ein Via mit dem rechten Anschluss abgeführt.
nicht-UND, oder?
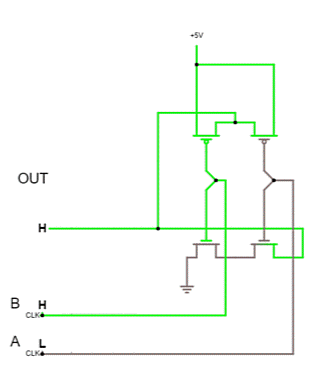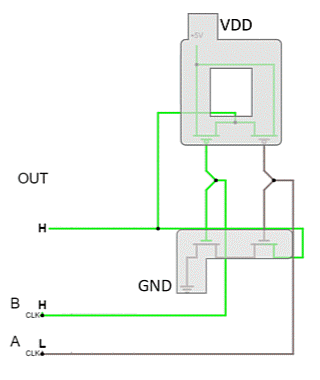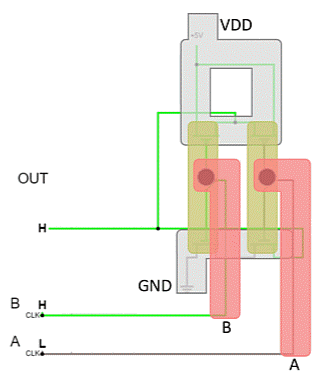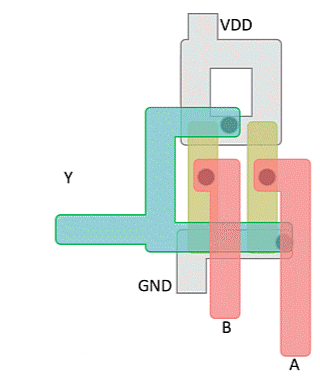
Wie funktioniert nun das NAND-Gatter, auf dem jegliche Logik aufgebaut werden kann? Das Konzept hinter diesem Gatter ist, dass der Ausgang nur logisch falsch ($Y=0$) ausgibt, wenn beide Eingänge auf logisch wahr ($A=1$ und $B=1$) steht. Das Gatter ist in figure 7 oben dargestellt. Dies muss über die beiden angesprochenen Transistortypen umgesetzt werden. Diese Struktur muss also so aufgebaut sein, dass:
- nur wenn beide Eingänge gleichzeig Transistoren mit $A=1$ und $B=1$ schalten, sollen $0V$ anliegen,
- wenn einer der Eingänge $A$ oder $B$, oder beide gleich 0 sind, soll $5V$ anliegen.
Ersteres ist über eine Hintereinanderschaltung der Transistoren an $0V$ möglich. Diese müssen bei einer Gatespannung von $5V$ (Eingang auf logisch $1$) die Source und Drain Anschlüsse kurzschließen, es sind also n-Kanal MOSFETs notwendig.
Letzteres benötigt eine Parallelschaltung von Transistoren gegen $5V$. Diese müssen mit einer Gatespannung von $0V$ Source und Drain kurzschließen. Hier werden p-Kanal MOSFETs genutzt (figure 7 unten).
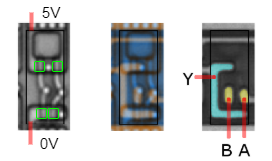
Die Umsetzung in Silizium (figure 8) erscheint auf den ersten Blick wieder etwas undurchsichtig. Auch in diesem Abbildung sind wieder drei Bilder zu sehen. Im ersten Bild sind die Transistoren wieder grün markiert und auch die Vias sind wieder über weiße Kreise zu erkennen. Betrachtet man die Darstellung genauer, fällt auf, dass der Via an $5V$ über den linken oder rechten MOSFET zu erreichen ist. Der Via an $0V$ ist aber nur zu erreichen, wenn beide unteren MOSFETs kurzschließen. Der Aufbau stimmt also mit der bisher ermittelten Schaltung überein. Die figure 9 und figure 10 sollen dies nochmals verdeutlichen.
eine einfache Rechnung
Wie können nun die NAND-Gatter so verschaltet werden, dass das Rechenwerk Operationen wie $y=a+b$ durchführen kann? Dazu wird die Operation zunächst nur für binäre Werte betrachtet. Um die binäre Größen von dezimalen Größen zu unterscheiden wird diesen ein $0b$ vorangestellt. Folgende Kombinationen sind also möglich:
- $0 + 0 = 0$ bzw. $0b0 + 0b0 = 0b00$
- $0 + 1 = 1$ bzw. $0b0 + 0b1 = 0b01$
- $1 + 0 = 1$ bzw. $0b1 + 0b0 = 0b01$
- $1 + 1 = 2$ bzw. $0b1 + 0b1 = 0b10$
Es ist zu sehen, dass nur wenn beide Eingänge gerade $1$ sind die zweite Stelle des Bitwertes gesetzt ist. Dies entspricht gerade einem AND. Da aber alles aus NAND-Gattern aufgebaut werden soll, muss eine geschickte Zusammenschaltung dieser Gatter gefunden werden. Hierzu wird einem NAND-Gatter ein Inverter-Gatter nachgeschalten. Das Inverter-Gatter wiederum erhält man über ein NAND-Gatter, wenn beide Eingänge verbunden werden. In figure 11 ist diese Schaltung unten durch die beiden unteren NAND-Gatter dargestellt.
Auch für die erste Stelle des Bitwertes lässt sich eine Schaltung finden. Wie kann man auf diese Schaltungen kommen? Dies wird im Kapitel Schaltnetze erklärt.
Werden viele Eingänge oder Ausgänge zusammengefasst, können größere Zahlenwerte umgesetzt werden. Das heißt, die Rechnung $3+3$ bzw. im binären $0b\color{green}1\color{violet}{1} + 0b\color{blue}{1}\color{red}{1}$ wird auf mehrere Einzelrechnungen heruntergebrochen. Dies ähnelt der händischen Addition durch Untereinanderschreiben der Zahlenwerte und schrittweiser Rechnung. In diesem Beispiel müsste zunächst $0b\color{violet}{1} + 0b\color{red}{1}$ berechnet werden, was $0b\boldsymbol{1}0$ ergibt. Im nächsten Schritt $0b\color{green}1 + 0b\color{blue}{1}$ muss zusätzlich noch der Überlauf aus der vorherigen Rechnung $0b\boldsymbol{1}$ berücksichtigt werden. So können prinzipiell beliebig lange Zahlen miteinander verknüpft werden.
Um die Zahlen handhabbarer für Mensch und Maschine zu gestalten wurde eine sinnvolle Gruppierung eingerichtet: 8 binäre Zahlenwerte werden zu einem Byte zusammengefasst. Dieses kann für Menschen lesbar als Dezimalwert $0...255$ oder Hexadezimalwert $0x00 ... 0xFF$ in Programmen dargestellt werden. Im Microprozessor werden diese Zahlenwerte stets als Binärwert gehandhabt.
Nano-Lego
weiterführende Links
- Eine schöne Übersicht der Kernideen zum Rechnen mit Strom ist vom Gymnasium Kirchenfeld (CH) zusammengestellt worden
- diverse Mikroskopaufnahmen auf SiliconZoo.org
- Erklärung zu CMOS in der englischen Wikipedia
- Wikiseite zu Integrierte Schaltkreise
Bildreferenzen
figure 1: TravisGoodspeed@Flickr CC BY 2.0
figure 2: ZeptoBars@Wikimedia,CC BY 3.0
figure 6, figure ##: SiliconZoo.org, Lizenz unbekannt
figure 9: David Carron@Wikimedia,public domain