Dies ist eine alte Version des Dokuments!

5. Storage Elements

In the previous chapter we have had a look onto memory devices, which store data even when no voltage is applied. This is great for longterm storage, like measurement data, pictures or music. The clock frequency of the storage element are often much lower than the internal frequency of the processor / controller. By this, the processor has to wait for the stored information due to high access time.

Therefore an controller-internal memory is advantageous. These are often called cache. Distinct storage elements have special properties, e.g. the written data changes the logic level of a pin ('foot') of the IC directly. We will now focus onto these controller-internal, fast memory, which consist of logic gates.

The name flipflop stems from the fact, that the smallest logic circuit for storing data has to store binary values. Therefore, it has to show one of two stable states, and can flip into the other one by an external interaction.

5.1 Evolution of a Flipflop

Flipflop as a Blackbox

In order to understand the wanted storage element, we will first look onto these element based on the IPO model (input–process–output).

The process of the storage element is to store two different states. This property can be implemented via two inverting gates which are interconnected in a feedback loop. The simple setup would be with NOT gates as shown in Abbildung 1.

Of course this simple elements misses inputs and outputs! Therefore we have to look into these now.

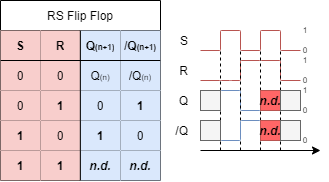
The input of this element needs at least two inputs. Often the following two are used:

• Set input: once this input is high, a $1$ is stored. This input is marked as $S$.
• Reset input: once this input is low, a $0$ is stored. This input is marked as $R$.

For the output also often two pins are shown. The pin $Q$ outputs the stored data directly. The pin $/Q$ outputs the inverted value.

Based on this simple requirements we can create the truth table.

• When $S=0$ and $R=0$, nothing changes and the outputs stay the same: $Q(n+1)=Q(n)$, $/Q(n+1)=/Q(n)$
• When $S=1$ and $R=0$, the stored information will be set: $Q(n+1)=1$, $/Q(n+1)=0$
• When $S=0$ and $R=1$, the stored information will be reset: $Q(n+1)=0$, $/Q(n+1)=1$
• When $S=1$ and $R=1$, it is unclear what to do.

In Abbildung 2 the last input ($S=1$, $R=1$) reaches a not defined state. This state have to be investigated more later.

RS flip flop - Open the Blackbox

First, the storage device have get some inputs in order to change the stored stage. For This, a „switchable“ NOT-gate is needed. Looking back to the chapter Boolean Algebra - Convertibility of Gates, this can be achieved by NAND gates or NOR gates.
In Abbildung 3 a first approach is shown.

But how are the inputs $X_0$ and $X_1$ related to $S$ and $R$, as well as the outputs $Q$ and $/Q$ to $Y_0$ and $Y_1$?
In this introduction, only flip flops based on NOR gates are discussed - but flip flops are can also be build up with NAND gates. In Abbildung 4 such a NOR flip flop is shown. Compared to Abbildung 3 the outputs had to be rearranged in order to have the pins sorted as shown in the logic symbol (see Abbildung 5)

So let's analyze how this setup works! Therefore, the circuit in Abbildung 4 has to be analyzed:

1. Initially, $Q=0$ and the both inputs are $0$. This is due to the facts, that:
   1. The upper NOR gate has also two $0$s as an input a outputs consequently $/Q=1$.
   2. This $1$ is also an input to the lower NOR gate.
   3. This respectively generates $Q=0$. This situation is stable.
2. When setting $S=1$ multiple things will happen successively:
   1. At first, the upper NOR gate has a $1$ on the input, which results into a $0$ at the output, and on $/Q$.
   2. With $/Q=0$ also both inputs of the lower NOR gate are $0$.
   3. Therefore, the lower gate generates $Q=1$.
3. The stored data is also stable:
   1. This means $Q=1$, even when going back to the initial state $S=0$ and $R=0$.
   2. The upper NOR gate still has one input set to $1$ and consequently still generates a $0$.
4. The only way to clear $Q$ (i.e. to set $Q=0$) is by setting $R=1$
   1. This this input the lower NOR gate has a $1$ as an input and outputs $Q=0$.
   2. By $Q=0$ the inputs of the upper NOR gate also both get $0$.
   3. This results in $/Q=1$

The only problem (or better inconsistency) appears, when setting both inputs to $1$:

• By this, both NOR gates generates $0$s
• This on the one hand creates $Q=1$ and $/Q=1$, which is not consistent.

This will get even more problematic:

• Both gates show typically not the exact same behaviour in respect to setting their outputs on a sub-microsecond scale to the voltage comparable with the logic $1$ or $0$.
• Therefore, once one will set the flip flop back to the initial state $S=0$ and $R=0$ both NOR gates compete to set their output to $1$. The faster one will win.
• This results in an arbitrary behavior.

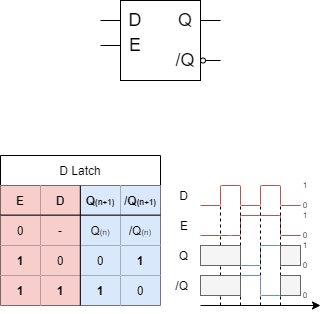
D-Latch - Solving the Inconsistencies

In order to solve this undefined behavior one simple solution is to have the reset input $R$ be always the negation of $S$. The input name is now changed to $D$, which refers to the stored data.

This single input solution is shown in Abbildung 6. The upper ciruit in Abbildung 6 shows a common problem: when the ciruict is not prepared correctly, the output could show an intermediate inconsistent situation. This can be seen for the switch from $D=0$ to $D=1$. For a short time the outputs are $Q=/Q=0$. A solution is to use a buffer (symbol „▷“). A buffer delays the signal for a similar timespan like a NOT-gate, but without negating the signal (shown in Abbildung 6 below).

However, this circuit rises a „small problem“: now the state can be changed, but set and reset is based on one single input. Therefore, it is not a storage device, but more a kind of a delay: when the input data changes, the output changes after a constant short timespan, too.
In order to solve this next problem, another input $E$ for enable is introduced (see Abbildung 7). Only for $E=1$ changes in the stored states are possible: For $E=1$ the circuit gets transparent. Once $E=0$, no changes in the state can be done.
The given circuitry is also called D-Latch with the symbol shown in Abbildung 8.

Generally, the term latch is used, when there is a transparent time span. Otherwise the circuit is called flip flop.

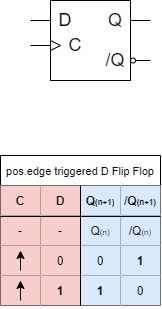
Edge-Triggered D Flip Flop - One at a time

In digital systems the data processing is done clocked (i.e. once in a cycle). In the sub-chapter before, the input $C$ was introduced. Once this input changes to $C=0$, the data could be used in the next logic stage.
Digital systems often need to be power efficient, in order to save energy and avoid overheating. A disadvantage of the D-latch is, that in the transparent phase, the signal can change often until it gets stored at the end of the phase. For every transistion, a small additional current flow is needed. Therefore, the D-latch is not as power efficient, and would also pass on the transistions to the next logic stages.

In order to change the full transparency into a single change per cycle, a circuit based on two D-latches in series can be used. In Abbildung 9 the two latches can be seen in the upper part. The first latch is enabled with the negated clock input $C$. Therefore, the first latch is only transparent for $C=0$. The second latch gets the double negated clock input, which means, it is only transparent for $C=1$. The output is changed (and $D$ is stored only for the switch from $C=0$ to $C=1$. By this, the state of $D$ is only stored, when switching $C$. When the switch from $C=0$ to $C=1$ is used, then this point in time is called positive edge.

The lower part in Abbildung 9 and Abbildung 10 shows the symbol of the D flip flop.

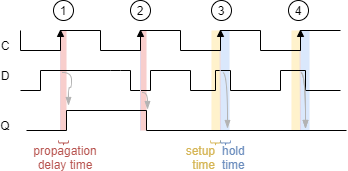
There are some important timing issues of all the flip flops and latches, which will discussed here.

1. Between the time of the triggering edge on $C$ and a resulting change in $Q$ the propagation delay time can be seen. This delay reflects the time for the flip flop to „process“ the data.

Examples

further Links

• https://www.electronics-tutorials.ws/sequential/seq_1.html
• https://www.electronics-tutorials.ws/counter/count_1.html