Inhaltsverzeichnis
Block 04 — Kirchhoff’s laws
4.0 Intro
4.0.1 Learning Objectives
- Identify nodes, branches, and (essential) loops in DC circuits and draw consistent reference arrows for $U$ and $I$ (passive/active sign conventions).
- State and apply Kirchhoff’s Current Law (KCL) at an arbitrary node and Kirchhoff’s Voltage Law (KVL) around a loop.
- Translate between verbal circuit descriptions and node/loop equations; check signs and units; solve for unknown currents/voltages in small networks.
- Use KCL/KVL as the foundation for upcoming techniques (series/parallel, dividers, bridges, source equivalents).
4.0.2 Preparation at Home
As always:
- Please read through the following chapter.
- Also here, there are some clips for more clarification under 'Embedded resources' (check the text above/below, sometimes only part of the clip is interesting).
For checking your understanding please do the following exercises:
- 2.3.3 (1)
- 2.4.3
4.0.3 90-minute Plan
- Warm-up (10 min): What is a “node”? what is a “mesh”? quick sketch-and-label drill.
- Core concepts (40 min): reference arrows & sign conventions → KCL at a node → KVL in a loop → dimensional check.
- Worked examples (20 min): one KCL node solve; one KVL loop solve with a source and two resistors.
- Guided practice (15–20 min): short tasks (incl. sims/drawings below).
- Wrap-up (5 min): checklist, common pitfalls, outlook to Block 05 (series/parallel, dividers, bridge).
4.1 Core Content
4.1.1 Nodes, Branches, and Loops
Electrical circuits typically have the structure of networks. Networks consist of two elementary structural elements:
- Branches (German: Zweige): Connections between two nodes.
- Node (German: Knoten): Connection „point“ of several branches.
Please note in the case of electrical circuits, we will use the following definition:
- Branches contain at least one component.
- Nodes connect more than two branches. Since the wire in a circuit diagram is an ideal conductor, all connected wires to a node are at the same voltage level. Therefore the node in the circuit diagram can also be spatially extended by the wires.
Sometimes there is a differentiation between „simple nodes“ (only connecting 2 branches) and „principal nodes“ (connecting more than 2 branches). We will in the following often only mark the connection of more than two branches with a node.
Branches in electrical networks are also called two-terminal networks. Their behavior is described by current-voltage characteristics and explained in more detail in block06.
In addition, another term is to be explained:
A loop begins and ends at the same node and runs over at least one further node.
Since a voltmeter can also be present as a component between two nodes, it is also possible to close a loop by a drawn voltage arrow (cf. $U_1$ in Abbildung 2).
Please keep in mind, that usually the entire behavior of networked circuits almost always changes when a change occurs in one branch or at one node. This is in contrast to other cause-effect relationships, but comparable to changes in other larger networks, e.g. a traffic jam in the road network, due to which other roads experience a higher load. For electrical engineering, this means that in the case of changing circuits, the focus is often on determining the interrelationships (formulas, current-voltage characteristics) and not on a single numerical value.
4.1.2 Reshaping Circuits
With the knowledge of nodes, branches, and meshes, circuits can be simplified. Circuits can be reshaped arbitrarily as long as all branches remain at the same nodes after reshaping The Abbildung 3 shows how such a transformation is possible.
For practical tasks, repeated trial and error can be useful. It is important to check afterward that the same components are connected to each node as before the transformation.
4.1.3 Kirchhoff’s Current Law (KCL)
In any node, the algebraic sum of currents is zero. All reference arrows are drawn either into or out of the node. \begin{align*} \boxed{\sum_{\nu=1}^{n} I_\nu = 0} \quad \end{align*}
Interpretation: the sum of currents flowing into a node equals the sum flowing out of that node → no net charge accumulation in steady DC.
Sign rule used here. If you write currents with reference arrows toward the node as positive, and away from the node as negative, KCL is $\sum I_x=0$. (Any one consistent choice is fine.)
Example / micro-exercise
At node $N$, suppose $I_1=2.00~{\rm A}$ and $I_2=0.50~{\rm A}$ flow into the node, and $I_3$ flows out of the node. With “into” positive: \begin{align*} I_1 + I_2 - I_3 = 0 \Rightarrow I_3 = 2.50~{\rm A}. \end{align*}
Units check: $[I]={\rm A}$ on every term, so the sum is consistent.
4.1.4 Parallel circuit of resistors
From Kirchhoff's current law, the total resistance for resistors connected in parallel can be derived (Abbildung 5):
Since the same voltage $U_{\rm ab}$ is dropped across all resistors, using Kirchhoff's current law:
$\large{{U_{\rm ab}}\over{R_1}}+ {{U_{\rm ab}}\over{R_2}}+ ... + {{U_{\rm ab}}\over{R_n}}= {{U_{\rm ab}}\over{R_{\rm eq}}}$
$\rightarrow \large{{{1}\over{R_1}}+ {{1}\over{R_2}}+ ... + {{1}\over{R_n}}= {{1}\over{R_{\rm eq}}} = \sum_{x=1}^{n} {{1}\over{R_x}}}$
Thus, for resistors connected in parallel, the equivalent conductance $G_{\rm eq}$ (German: Ersatzleitwert) is the sum of the individual conductances: $G_{\rm eq} = \sum_{x=1}^{n} {G_x}$
In general: the equivalent resistance of a parallel circuit is always smaller than the smallest resistance.
Especially for two parallel resistors $R_1$ and $R_2$ applies:
\begin{align*} \boxed{R_{\rm eq}= R_1 || R_2 = \large{{R_1 \cdot R_2}\over{R_1 + R_2}} } \end{align*}
4.1.5 Current divider
The current divider rule shows in which way an incoming current on a node will be divided into two outgoing branches.
The rule states that the currents $I_1, ... I_n$ on parallel resistors $R_1, ... R_n$ behave just like their conductances $G_1, ... G_n$ through which the current flows.
\begin{align*} \large{{I_1}\over{I_{\rm res}}} = {{G_1}\over{G_{\rm res}}} \large{{I_1}\over{I_2}} = {{G_1}\over{G_2}} \end{align*}
The rule also be derived from Kirchhoff's current law:
- The voltage drop $U$ on parallel resistors $R_1, ... R_n$ is the same.
- When $U_1 = U_2 = ... = U$, then the following equation is also true: $R_1 \cdot I_1 = R_2 \cdot I_2 = ... = R_{\rm eq} \cdot I_{\rm res}$.
- Therefore, we get with the conductance: ${{I_1} \over {G_1}} = {{I_2} \over {G_2}}= ... = {{I_{\rm eq}} \over {G_{\rm res}}}$
4.1.6 Kirchhoff’s Voltage Law (KVL)
Around any closed loop, the algebraic sum of voltages is zero: \begin{align*} \boxed{\sum_{\nu=1}^{n} U_\nu = 0} \quad \end{align*}
Equivalently: the sum of rises equals the sum of drops along the chosen loop direction. The result does not depend on the specific path between two nodes.
Sign rule used here. Choose a loop direction (often clockwise). A voltage arrow aligned with the loop direction is added; opposed to it is subtracted. (Source polarities must respect the active/passive conventions fixed earlier.)
Example / micro-exercise
Series loop with source $U_{\rm s}=12.0~{\rm V}$, resistors $R_1=3.0~\Omega$, $R_2=5.0~\Omega$. With passive sign convention across both resistors and loop direction from the $+$ of the source: \begin{align*} -U_{\rm s} + U_{R_1} + U_{R_2} = 0, \quad U_{R_k} = R_k I. \end{align*}
Thus
$I = \frac{U_{\rm s}}{R_1+R_2} = \frac{12.0~{\rm V}}{8.0~\Omega}=1.50~{\rm A}$
$U_{R_1}=4.50~{\rm V}$, $U_{R_2}=7.50~{\rm V}$
$-12.0~{\rm V}+4.50~{\rm V}+7.50~{\rm V}=0$. (Check: volts add algebraically to $0$.)
Series circuit of resistors
Using Kirchhoff's voltage law, the total resistance of a series circuit (in German: Reihenschaltung, see Abbildung 7) can be easily determined:
\begin{align*} U_1 + U_2 + ... + U_n = U_{\rm res} R_1 \cdot I_1 + R_2 \cdot I_2 + ... + R_n \cdot I_n = R_{\rm eq} \cdot I \end{align*}
Since in a series circuit, the current through all resistors must be the same - i.e. $I_1 = I_2 = ... = I$ - it follows that:
\begin{align*} R_1 + R_2 + ... + R_n = R_{\rm eq} = \sum_{x=1}^{n} R_x \end{align*}
In general: The equivalent resistance of a series circuit is always greater than the greatest resistance.
4.1.7 From laws to tools (preview)
KCL and KVL immediately yield:
- Series: same current through all series elements $\Rightarrow$ voltages add, $R_{\rm eq}=R_1+R_2+\dots$.
- Parallel: same voltage across all parallel elements $\Rightarrow$ currents add, $G_{\rm eq}=G_1+G_2+\dots$.
- Dividers and bridge behavior follow from the same laws. (We will formalize these in Block05.)
For orientation, the short slides you cross-check with present the same sequence: KCL/KVL → resistive networks → (later) real sources and two-port models.
4.2 Common pitfalls
- Mixed conventions: do not swap passive/active mid-solution. Fix reference arrows once, then stick to them.
- Sign slips: in KVL, mark loop direction on the drawing; in KCL, decide “in is $+$” (or “out is $+$”) and keep it for *all* terms.
- Units: always write ${\rm A}$ for currents and ${\rm V}$ for voltages in interim and final results.
4.3 Exercises
Exercise 2.3.1 Branches and Nodes
For the markings in the circuits in Abbildung 8 indicate whether it is a branch, a node, or neither.
Exercise 2.3.2 Branches and Nodes (with explanation)
Exercise 2.3.3 Reshaping circuits
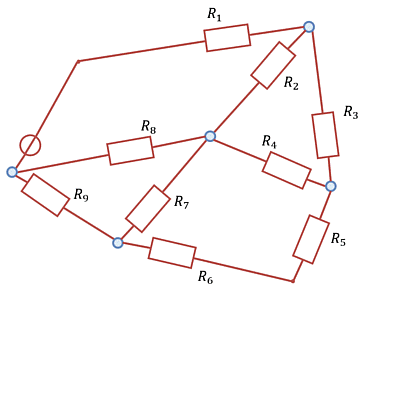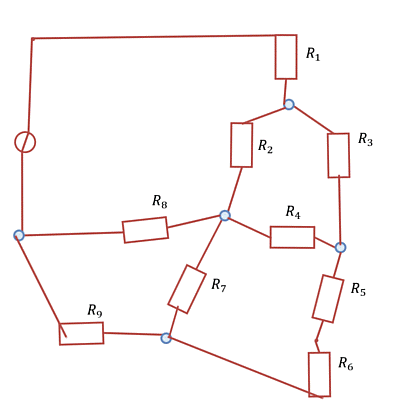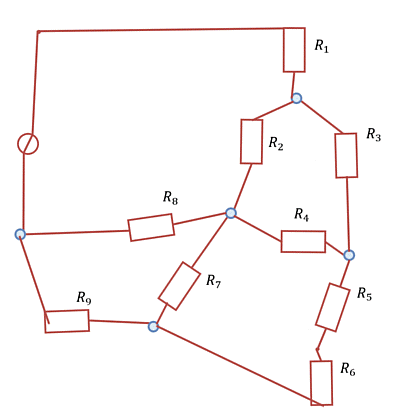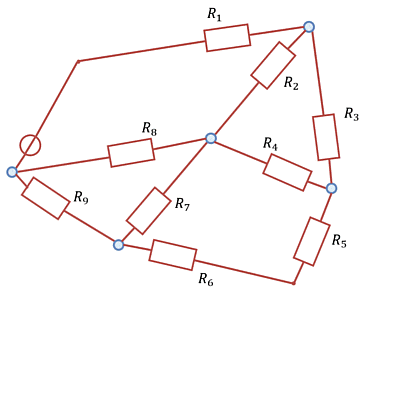
Reshape the circuits in Abbildung 9.
Exercise 2.4.1 Current divider
In the simulation in Abbildung 10 a current divider can be seen. The resistances are just inversely proportional to the currents flowing through it.
- What currents would you expect in each branch if the input voltage were lowered from $5~\rm V$ to $3.3V~\rm $? After thinking about your result, you can adjust the
Voltage(bottom right of the simulation) accordingly by moving the slider. - Think about what would happen if you flipped the switch before you flipped the switch.
After you flip the switch, how can you explain the current in the branch?
Exercise 2.4.2 two resistors
Two resistors of $18~\Omega$ and $2~\Omega$ are connected in parallel. The total current of the resistors is $3~\rm A$.
Calculate the total resistance and how the currents are split to the branches.
Exercise 4.3 KVL in a loop (source + two resistors)
Sketch a loop with $U_{\rm s}=5.00~{\rm V}$, $R_1=1.00~{\rm k\Omega}$, $R_2=1.00~{\rm k\Omega}$. Draw passive arrows across both resistors and choose clockwise loop direction.
Write KVL, solve $I$, then compute $U_{R_1}$ and $U_{R_2}$. Confirm that algebraic sum equals $0~{\rm V}$.
*Expected:* $I=2.50~{\rm mA}$, $U_{R_1}=2.50~{\rm V}$, $U_{R_2}=2.50~{\rm V}$.
Exercise 2.4.3 Three Resistors
Three equal resistors of $20~k\Omega$ each are given.
Which values are realizable by the arbitrary interconnection of one to three resistors?
Embedded resources
Explanation of the different network structures
(Graphs and trees are only needed in later chapters)
Reshaping circuits
Derivation of the current divider with examples
Summary
- KCL: sum of signed currents at any node is $0$ (charge does not pile up in steady DC).
- KVL: sum of signed voltages around any loop is $0$ (potential differences are path-independent).
- Conventions matter: fix passive/active sign conventions once, then *stay consistent*.
- Next: apply KCL/KVL to build series/parallel laws, dividers, and bridges (Block 05); then model real sources and two-port equivalents.