Inhaltsverzeichnis
3 Basic circuits of operational amplifiers I
- Operational amplifier basic circuits provide a nice introduction.
- Operational Amplifiers (Johan Huijsing) [viewable via the university network]
- On Youtube the following videos are recommended: What is an operational amplifier?, Inverting operation amplifier circuit, Non-inverting operation amplifier circuit.
Introductory example
Acoustic amplifiers, such as those found in mobile phones, laptops, or hi-fi systems, often exhibit an unpleasant characteristic when heavily amplified: the previously undistorted signal is no longer passed on as usual, but clatters. It is distorted in such a way that it no longer sounds pleasant.
For this purpose, you will find an acoustic example with pictures in Abbildung 1 and Abbildung 2 respectively. The bottom of each image shows the time course of the voltage output to a loudspeaker (x-axis: time, y-axis: frequency). The upper picture has three dimensions: It shows in color intensity which frequencies are used at which time. The frequencies in grey areas are not used. If a frequency is shown in red at one point in time, it has a relatively large amplitude.
It can be seen that the distorted signal has large amplitudes in the time course of the voltage as well as a wide distribution of frequencies (= a broad spectrum). The high frequencies in particular can promote wear of the diaphragm in loudspeakers.
The signal distortion is due to the design of the amplifier, which can only output the maximum possible voltage and otherwise clipping. The structure of an acoustic amplifier is similar to that of a feedback operational amplifier, as seen in the simulation.
Acoustic amplifiers are usually constructed like operational amplifiers, which will be considered in this chapter.
Objectives for basic circuits of operational amplifiers
After this lesson you should:
- Have learned the basic equation of operational amplifiers and the golden rules.
- Know how the basic circuits (inverting and non-inverting amplifiers) are constructed, what their voltage gain is, and how their input and output resistances behave.
- Be able to calculate the voltage gain of simple amplifier circuits.
- Understand the concept of virtual ground.
3.0 Introduction
Historical outline
To understand the origin of the operational amplifier, a brief outline of microprocessor history will be presented here. The first microprocessor was commercially distributed in 1971 by INTEL as Intel 4004, which could only represent a 4-bit number space with one word and had a clock frequency of 500 kHz. This was already extended after half a year as 8008 on an 8-Bit word so that calculations could be accomplished substantially faster. From this second generation, the 8086 was developed in 1978, which had been the basis of many PCs and other electronic components with a 16-bit word for a very long time. In 1985 this processor was extended from 80386 to a 32-Bit Word. From this time also the perhaps well-known question originates whether software should be installed as x86 or x64 code. Processors with 64-bit Word have been available since 1999, but they have not yet penetrated all niches.
With this historical outline in mind, the question arises as to how Apollo 11 was able to control both the first lunar mission and the lunar module, and how the orbit could be calculated so accurately that this would not pose a risk. Development of the Apollo Guidance Computer was started in 1961, 10 years before the first commercial microprocessor. This processor, with about 1MHz frequency and 16-bit word width, could provide performance as early as 1966 that was not commercially available until 15 years later. Nevertheless, these computers could not solve the differential equation systems necessary for trajectory planning in a reasonable amount of time. This was only possible by combining the well-known digital processor and the analog computers that had been in use since the 1920s. Analog computers are only slightly reminiscent of the classical image of the computer. Although they also consist of a network of components, they do not have any software. Rather, various properties of electronic components are used for computation (e.g., the exponential behavior of the Shockley equation of the diode). For the Apollo missions, the EAI 380 hybrid computer was used. This and similar hybrid computers continued to be used into the 1990s to solve systems of differential equations for aerospace, construction, and (under a slightly different guise) as synthesizers in the music industry. The interested reader is referred to the video Analog computers, which explains why they are superior to even the most modern computers.
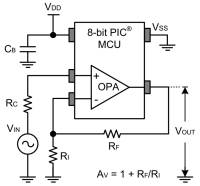 Abb. 4: Operational Amplifier Module (OPA) in a PIC microcontroller manufactured by Microchip (c) Microchip
Abb. 4: Operational Amplifier Module (OPA) in a PIC microcontroller manufactured by Microchip (c) Microchip
The core component of analog computers is the operational amplifier. With this, it is possible to build and combine adders, subtractors, multipliers, exponentials, integrators, and differentiators. The „calculation“ happens almost instantaneously after setting the desired input voltages.
The operational amplifier has outlasted this time and nowadays offers a starting point for a wide variety of signal conditioning, such as active filters, amplifier stages, input/output resistance matching, and various (integrated) control loops. Several microcontrollers have op-amps built right in and can be configured by suitable code. In Abbildung 4 a PIC microprocessor is shown, which contains an integrated operational amplifier.
3.1 Circuit symbols and basic circuitry
This chapter deals with operational amplifiers or in general with measuring amplifiers. One application for this is the measurement of voltages, currents, and resistances. These must be determined very precisely in some applications, for example for accurate temperature measurement. In this case, amplification of the measurement signals is useful and necessary.
This amplification is done by measuring amplifiers. Measuring amplifiers have to fulfill some characteristics:
- Measurement amplifiers should not have any feedback effect on the measured variable. An operational amplifier should have the highest possible input resistance. This prevents the voltage to be amplified from collapsing.
- Measuring amplifiers should have a high sensitivity. An operational amplifier should have a large differential gain $A_\rm D$.
- Measuring amplifiers should show a defined transmission behavior, i.e. the output signal should be clearly related to the input signal. An operational amplifier concretely should show a linear relationship.
- Measuring amplifiers should show good dynamic behavior. The output signal of an operational amplifier should follow the input signal without any time delay.
- Measurement amplifiers should produce an „impressed output signal“. This means that the components at the amplifier output cannot change the output signal. An operational amplifier, specifically, should be able to maintain the desired output signal with the necessary current to do so. Since the current $I_\rm O$ can become very large (by electronic standards), this means that an operational amplifier must have a low output resistance $R_{\rm O} =\frac{U_{\rm O}}{I_{\rm O}}$.
In general, a measurement amplifier is constructed as in Abbildung 5. This has already been described in chapter Amplifier Basics. In the following, only operational amplifiers will be considered. An operational amplifier is a measurement amplifier, which is often used in electrical engineering.
The circuit symbol of the amplifier is an isosceles triangle, at the apex of which the output signal originates and at the base of which the input signal enters. In Abbildung 6 you can see different circuit symbols:
- Circuit symbol (1): In block diagrams (not to be confused with circuit diagrams, see chapter 1) this circuit symbol is used for general amplifiers. The input signal enters an input and exits through an input. This symbol will not be found again until Chapter 5.
- Circuit symbol (2): According to DIN EN 60617, this circuit diagram is to be used for operational amplifiers. It indicates with the infinity sign the ideally infinitely high amplification. in the following this symbol is not used, because it is not used in all international circuits and tools.
- Circuit symbol (3): The circuit symbol (3) is the most commonly used symbol for an operational amplifier. On the left is the inverting input with voltage $U_{\rm m}$ (minus) and the non-inverting input with $U_{\rm p}$ (plus). The output with voltage $U_{\rm O}$ is shown on the right.
- Circuit symbol (4): The circuit symbol (4) is additionally drawn with the supply voltages $U_{\rm sp}$ (supply plus) and $U_{\rm sm}$ (supply minus). Power is provided from the supply for the output voltage of the operational amplifier.
- Circuit symbols (5) and (6): these symbols show no operational amplifier. These symbols show the NOT gate and the tri-state gate. Both of these components have already been discussed in fundamentals of digital engineering. Unfortunately, the representation of these digital components in various circuits is not unlike the operational amplifier. An example of this is the transceivers1) SP3481 or SP3485. If digital input values are considered, assuming that the circuit symbol does not represent an operational amplifier.
Notice: opamp input
The inputs of the operational amplifier are designated as inverting input $U_\rm m$ and non-inverting input $U_\rm p$.
The voltage $U_{\rm D} = U_{\rm p} - U_{\rm m}$ is called the differential voltage (see Abbildung 7).
3.2 Basic Equation / Golden Rules
The operational amplifier is a voltage amplifier. Thus it follows from the chapter idealized amplifier basic types that for the ideal case, the input resistance must be infinite and the output resistance $R_{\rm O}=0$.
The Abbildung 8 shows an ideal voltage amplifier. This is characterized by the following properties:
- input resistance: The input side is drawn in the figure. The resistance given here is the differential resistance $R_{\rm D}$ where the differential voltage $U_{\rm D}$ drops. Therefore $R_{\rm D} \rightarrow \infty$ is valid. Thus, the input currents $I_\rm p \rightarrow 0$ and $I_\rm m \rightarrow 0$.
- Output resistance, Basic equation: On the output side, $R_\rm O=0$ gives that $U_{\rm O} = A_{\rm D}\cdot U_\rm D$. This is the basic equation of the amplifier circuit. Ideally, the op-amp amplifies linearly, as indicated in the equation. Specifically, for a differential voltage of $0 ~\rm V$, the output voltage is $0 ~\rm V$.
- Voltage Gain: From the chapter feedback it is known that $A_\rm D$ must be very large. Ideally, the following applies: $A_ \rm D \rightarrow \infty$
Remember: basic equation and golden rules
- The output voltage depends on the differential voltage via the differential gain: $U_{\rm O} = A_{\rm D} \cdot U_\rm D$ This is the basic equation of the amplifier circuit.
- The golden rules of the ideal amplifier are:
- The differential gain goes to infinity: $A_\rm D \rightarrow \infty$
- The input resistance goes to infinity: $R_\rm D \rightarrow \infty$
- The output resistance is 0: $R_\rm O = 0$
These rules have different limits in the real amplifier:
- $\boldsymbol{U_{\rm O} = A_{\rm D} \cdot U_{\rm D}}$:
- The output voltage can only follow the input voltage as far as the power supply allows. In real operational amplifiers, only so-called rail-to-rail operational amplifiers can exploit the range down to a few $100 ~\rm mV$ to $U_\rm S$. Other operational amplifiers have an output limit, which is $1 ... 2 ~\rm V$ below the supply voltage.
- If the supply voltages are not symmetrical ($U_{\rm sm} \neq -U_{\rm sp}$), then the characteristic also shifts.
- The ideal operational amplifier produces the same output voltage $U_{\rm O}=A_{\rm D} \cdot U_{\rm D}$ as long as $U_{\rm D} = U_{\rm p} - U_{\rm m}$ is the same. For the real operational amplifier with fixed $A_{\rm D}$, output voltage $U_{\rm O1}$ for $U_{\rm D1}=5 ~\rm V - 4.9 ~V$ is different from $U_{\rm O2}$ for $U_{\rm D1}=0.1 ~\rm V - 0 ~V$.
- $\boldsymbol{A_\rm D}$: The differential gain is usually between $A_\rm D = 20'000 ... 400'000$.
- $\boldsymbol{R_\rm D}$: For real operational amplifiers, the input resistance $R_\rm I > 1 M\Omega$ and the input current $|I_\rm p|$ or $|I_ \rm m|$ is less than $1 ~\rm µA$.
- $\boldsymbol{R_\rm O}$: In real operational amplifiers, the output resistance $R_\rm O$ is usually a few $\Omega$ and limited by a maximum current (in the range of a few tens of $\rm mA$ to a few $\rm A$)
The op-amp in the simulation replicates a real op-amp in some respects: The voltage gain is $A_\rm D = 100'000$. The transfer characteristic $U_{\rm O}(U_\rm D)$ shows proportional behavior only when the output value is smaller in magnitude than the supply voltage $|U_{\rm sp}|=|U_{\rm sm}|=15 ~\rm V$ (not shown). The modulation limits and the voltage gain can be changed in the simulation via „Edit component“ (double click).
Power supply of the operational amplifier
For the voltage supply of the operational amplifier, a distinction is made between unipolar and bipolar:
With the bipolar voltage supply, the same voltage levels but with different signs are applied to both supply terminals in terms of magnitude (Abbildung 9 (1)). This allows the output voltage $U_{\rm O}$ of the amplifier to point in either direction (Abbildung 9 (2)). The power supply must be designed in such a way that it can provide both voltages. A differential voltage of $U_{\rm D}=0$ also results in an output voltage of $U_{\rm O}=0$.
With the unipolar power supply, the negative supply terminal is connected to the ground (Abbildung 9 (3)). As a result, the output voltage $U_{\rm O}$ of the amplifier can only take on non-negative values (Abbildung 9 (4)). In this case, the supply can be provided by a single voltage source (e.g., a battery). With a differential voltage of $U_\rm D=0$, the output voltage is $U_{\rm O}=\frac{1}{2}\cdot U_{\rm sp}$.
3.3 Voltage follower
In the chapter feedback it was described that an amplifier with high open-loop gain can be „tamed“ by feeding back a part of the output signal with a negative sign. In the simplest case, the output signal could be fed directly to the negative input of the operational amplifier. The input signal $U_\rm I$ of the entire circuit is applied to the positive input. In Abbildung 10 this circuit is shown.
Using this circuit, the procedure for solving amplifier circuits is now to be illustrated.
- The aim is always to create a relation between output voltage $U_\rm O$ and input voltage $U_ \rm I$. Thus, the goal here is the voltage gain $A_{\rm V}=\frac{U_{\rm O}}{U_\rm I}$.
- Before calculating, it should be checked how many equations describe the system and thus have to be set up. This can be determined by the number of variables. This is done by counting through the currents and voltages of the circuit. In this case, there are 3 currents and 3 voltages. So the number of equations needed is 6.
- Now equations are set up that can be used. These are:
- Basic equation: (1) $U_{\rm O} = U_{\rm D} \cdot A_\rm D$
- Golden rules: $R_\rm D \rightarrow \infty$ so that (2+3) $I_{\rm p} = I_{\rm m} = 0$, $A_{\rm D} \rightarrow \infty$, $R_\rm O = 0$
- Consideration of the existing loops: in this example, there is only one loop (4) $-U_{\rm I} + U_{\rm D} + U_{\rm O} = 0$. Caution: loops can not enter the amplifier through input and exit through the output! Also to be noted is the direction of $U_{\rm D}$.
- Consideration of the existing nodes: in this example, there is only one node (5) $I_{\rm o} = I_m$.
- There appears to be a missing equation. However, this is not correct, because there is still an equation hidden in the objective: (0) $A_{\rm V}=\frac{U_{\rm O}}{U_\rm I}$
- Now, to solve the equations, the equations must be cleverly inserted into each other in such a way that there are no dependencies on the variables left at the end.
The calculation is done here once in detail (clicking on the arrow to the right „►“ leads to the next step, alternative representation):
So the voltage gain is $A_\rm V = 1$. This would also have been seen in chapter feedback. There it was derived that for $A_\rm D \rightarrow \infty$ the voltage gain just results from $k$: $A_{\rm V}=\frac{1}{k}$. Since the entire output voltage is fed back here, $k=1$ and thus also $A_\rm V=1$.
The output voltage $U_\rm O$ is therefore equal to the input voltage $U_\rm I$. This is where the name „voltage follower“ comes from. Now one could assume, that this amplifier is of little help because also a direct connection would deliver $U_{\rm O}=U_{\rm I}$. But the important thing here is: because of the operational amplifier, there is no feedback from U_O to U_I. This means that a resistor on the output side will not load the input side. In the simulation, the „Resistance“ slider (on the right) can be used to change the load resistance. This changes the current flow, but not the voltage.
This behavior can also be explained in another way: The input signal usually comes from a voltage source, which can only produce low currents. That means the input signals are high impedance ($\text{high impedance}=\frac{\text{voltage}}{\text{low current}}$). However, a load of arbitrary impedance can be applied to the output. That is, to keep the output signal constant, a large current must be provided depending on the load. As the output resistance of the amplifier approaches 0, the signal is low impedance ($\text{low impedance}=\frac{\text{voltage}}{\text{(likely) large current}}$). This is where the second name of the circuit „impedance converter“ comes from.
Remember: steps to the goal
To solve tasks, the following procedure helps:
- Where to? Clarification of the goal (here: always the relation between output and input signal)
- What to? Clarification of what is needed (here: always equations. The number of needed equations can be determined by the number of variables)
- With what? Clarification of what is already available (here: known equations: voltage amplification equation, basic equation, golden rules, loop/node theorem, relationships of voltages and currents of components).
- Go. Work out the solution (here: inserting the equations) It helps to rearrange the equation so that $1/A_\rm D$ appears without a prefactor. It is valid: $1/A_{\rm D} \xrightarrow{A_{\rm D} \rightarrow \infty} 0$
3.4 Non-inverting amplifier
So far, the entire output voltage has been negative-feedback. Now only a part of the voltage is to be fed back. To do this, the output voltage can be reduced using a voltage divider $R_1+R_2$. The circuit for this can be seen in Abbildung 11.
By considering the feedback, the result can be quickly derived here as well: only $\frac{R_2}{R_1+R_2}\cdot U_{\rm O}$ is fed back from the output voltage $U_{\rm O}$. So the feedback factor is $k=\frac{R_2}{R_1+R_2}$ and thus the voltage gain becomes $A_{\rm V}=\frac{R_1+R_2}{R_2}$.
This „trick“ via $A_{\rm V}=\frac{1}{k}$ is no longer possible for some of the following circuits. Accordingly, a possible solution via network analysis is to be derived here as well.
Exercise 3.4.1 non-inverting amplifier
For the non-inverting amplifier, derive the voltage gain. Use the procedure that was used for the voltage follower..
| Step | Description | Implementation |
|---|---|---|
| 1 | What is wanted? | $A_{\rm V} = \frac{U_{\rm O}}{U_{\rm I}}=?$ |
| 2 | Counting the variables $\rightarrow$ Number of equations needed | 5 voltages + 5 currents $\rightarrow$ Number of equations needed: 10 |
| 3 | Setting up the equations | (1) Basic equation: $U_{\rm O} = A_{\rm D} \cdot U_{\rm D}$
Golden rules: $R_\rm D \rightarrow \infty$ so that (2+3) $I_\rm p \rightarrow 0$ and $I_\rm m \rightarrow 0$ $R_{\rm O} = 0$ $A_\rm D \rightarrow \infty$ (see ) (4) Loop I: $-U_{\rm I} + U_{\rm D} + U_2 = 0$
(5) Loop II: $-U_2 -U_1 + U_{\rm O} = 0$ (6) Node I: $I_{\rm o} = I_1$ (7) Node II / voltage divider: $I_1 - I_2 - I_\rm m = 0$
(8) Resistor $R_1= \frac{U_1}{I_1}$ (9) Resistor $R_2= \frac{U_2}{I_2}$ |
The calculation is done here again in detail (clicking the right arrow „►“ leads to the next step, alternative representation):
So the voltage gain of the non-inverting amplifier is $A_{\rm V}=\frac{R_1+R_2}{R_2}$ or $A_{\rm V}=1+\frac{R_1}{R_2}$. Thus, the numerical value $A_{\rm V}$ can only become larger than 1. This is shown again in the simulation. In real circuits, the resistors $R_1$ and $R_2$ will be in the range between a few $100 ~\Omega$ and a few $\rm M\Omega$. If the sum of the resistors is too small, the operational amplifier will be heavily loaded. However, the output current must not exceed the maximum current. If the sum of the resistors is too large, the current $I_1 = I_2$ can come into the range of the current $I_\rm m$, which is present in the real operational amplifier.
The input and output resistance of the entire circuit should also be considered here. Both resistors are marked here with a superscript 0 to distinguish them from the input and output resistance of the operational amplifier. The input resistance $R_{\rm I}^0$ is given by $R_{\rm I}^0=\frac{U_\rm I}{I_\rm I}$ with $I_{\rm I}=I_\rm p$. Thus, for the ideal operational amplifier, it is also true that the input resistance $R_{\rm I}^0=\frac{U_\rm I}{I_\rm p} \rightarrow \infty$ becomes when $I_\rm p \rightarrow 0$.
In the real case it is important in how far the total input resistance depends on the input resistance of the operational amplifier $R_{\rm I}^0(R_\rm D)$. This can be derived as follows: (clicking on the right arrow „►“ leads to the next step, alternative representation):
So it can be assumed simplistically, that the input resistance of the whole circuit is many times higher than the input resistance of the operational amplifier. The output resistance $R_\rm O^0$ of the whole circuit with real operational amplifiers shall only be sketched: In this case, the output resistance $R_\rm O$ of the operational amplifier is in parallel with $R_1 + R_2$. Thus the output resistance $R_\rm O^0$ will be somewhat smaller than $R_\rm O$.
Notice: non-inverting amplifier
For the non-inverting amplifier, the following holds:
- The input voltage $U_\rm I$ is at the non-inverting input of the operational amplifier.
- The feedback is done by a voltage divider $R_1 + R_2$
- The voltage gain is $A_{\rm V}=\frac{R_1+R_2}{R_2}$ or $A_{\rm V}=1+\frac{R_1}{R_2}$ and is always greater than 1.
- Both input and output resistances of the overall circuit are smaller than those for the (real) operational amplifier used.
3.5 Inverting Amplifier
The circuit of the inverting amplifier can be derived from that of the non-inverting amplifier (see Abbildung 13). To do this, first consider the noninverting amplifier as a system with 3 connections (or as a quadripole): $U_\rm I$, $\rm GND$, and $U_\rm O$. These terminals can be rearranged - while keeping the output terminal $U_\rm O$.
Thus the voltage divider $R_1 + R_2$ is no longer between $U_\rm O$ and $\rm GND$, but between $U_\rm O$ and $U_\rm O$, see Abbildung 12. In this circuit, the resistor $R_2$ is also called the negative feedback resistor.
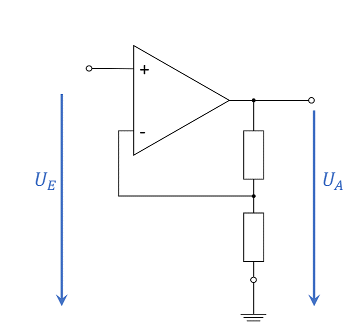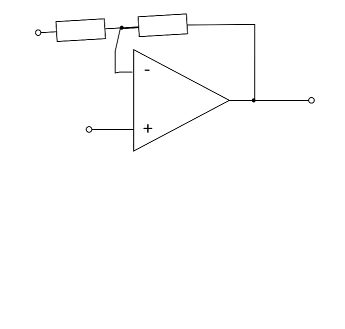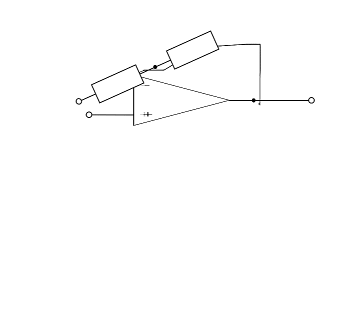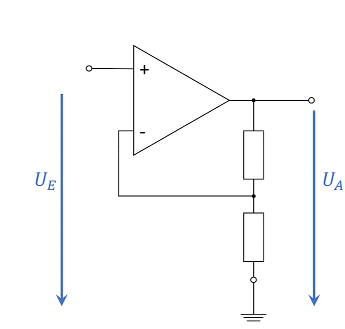 Abb. 13: Converting non-inverting amplifier to inverting amplifier. U_E is the input voltage (Eingangsspannung), U_A is the output voltage (Ausgangspannung).
Abb. 13: Converting non-inverting amplifier to inverting amplifier. U_E is the input voltage (Eingangsspannung), U_A is the output voltage (Ausgangspannung).
Before the voltage gain is determined, the node $\rm K1$ in Abbildung 12 is to be considered first. This is just larger than the ground potential by the voltage $U_\rm D$; thus, it lies on the potential difference $U_\rm D$. For a feedback amplifier with finite voltage supply, $U_\rm O$ can only be finite, and thus $U_{\rm D}= U_{\rm O} / A_{\rm D} \rightarrow 0$ (cf. basic_equation of the operational amplifier), since $A_D \rightarrow \infty$ holds. Thus it can be seen that the node $\rm K1$ is always at ground potential in the ideal operational amplifier. This property is called virtual ground because there is no direct short to ground. The op-amp regulates its output voltage $U_\rm O$ in such a way that the voltage divider sets a potential of $0~\rm V$ at node $\rm K1$. This can also be seen in the simulation by the voltage curve at $\rm K1$.
The following diagram shows again the interactive simulation.
$R_{\rm 1}$ and $R_{\rm 2}$ can be manipulated by the sliders. Hit Run / STOP to run
Notice: virtual ground
For the ideal feedback amplifier, $U_\rm D \rightarrow 0$ holds. This means that the same voltage is always present at both inputs. if one of the two voltages is fixed, for example by connecting ground potential or even by a fixed voltage source, this property is called virtual ground.
For the determination of the voltage gain, the consideration of the feedback $A_{\rm V}=\frac{1}{k}$ seems to be of little use at first. Instead, however, the determination via network analysis is possible. Abbildung 12 shows a possible variant to choose the loops for this purpose. However, network analysis is not to be done here, but is given in Exercise 3.5.1 below.
Instead, two other ways of derivation will be shown here to bring further approaches closer. For the first derivation, the voltage divider $\boldsymbol{R_1 + R_2}$ is considered. For the unloaded voltage divider, the general rule is:
\begin{align*} U_2 = U_{12} \cdot \frac{R_2}{R_1 + R_2} \end{align*}
This equation is now to be adapted for concrete use. First Abbildung 12, the voltages of the voltage divider can be read as given in Abbildung 14. From this, using the general voltage divider formula:
\begin{align*} U_2 = ( U_I - U_O ) \cdot \frac{R_2}{R_1 + R_2} \end{align*}
With the virtual mass at node $\rm K1$ in Abbildung 14, it holds that $U_2$ points away from the (virtual) mass and thus $U_2 = U_\rm O$. Similarly, $U_{\rm I} = U_1$ holds. Thus it follows:
\begin{align*} - U_{\rm O} = ( U_{\rm I} - U_{\rm O} ) \cdot \frac{R_2}{R_1 + R_2} \end{align*}
And from that:
\begin{align*} - U_O &= U_I \cdot \frac{R_2}{R_1 + R_2} - U_O \cdot \frac{R_2}{R_1 + R_2} \\ - U_O + U_O \cdot \frac{R_2}{R_1 + R_2} &= U_I \cdot \frac{R_2}{R_1 + R_2} \\ U_O \cdot (\frac{R_2}{R_1 + R_2}-1) &= U_I \cdot \frac{R_2}{R_1 + R_2} \\ \frac{U_O}{U_I} &= \frac{\frac{R_2}{R_1 + R_2}}{\frac{R_2}{R_1 + R_2}-1} \\ \frac{U_O}{U_I} &= \frac{R_2}{R_2 - (R_1 + R_2)} = \frac{R_2}{-R_1} \\ \\ \boxed{ A_V = - \frac{R_2}{R_1}} \end{align*}
For the second derivation, the current flow through the resistors $R_1$ and $R_2$ of the unloaded voltage divider is to be considered. These two currents $I_1$ and $I_2$ are just equal. Thus:
\begin{align*} I_\boxed{}=\frac{U_\boxed{}}{R_\boxed{}}=const. \quad \text{with} \: \boxed{}=\{1,2\} \end{align*}
respectively
\begin{align*} \frac{U_1}{R_1}=\frac{U_2}{R_2} \end{align*}
This can also be converted into a „seesaw“ or mechanical analog via like triangles. In the mechanical analog, the potentials are given by height. As in the electrical case with the ground potential, a height reference plane must be chosen in the mechanical picture. The electric currents correspond to forces (i.e., a momentum flux) - but the consideration of forces is not necessary here. 2).
Now, if a certain height (voltage $U_\rm I$) is set, a certain height on the right side (voltage $U_\rm O$) is obtained via the force arm (resistor $R_1$) and load arm (resistor $R_2$). This is shown in Abbildung 15 above. In the figure, all points marked in red () can be manipulated. Accordingly, the input voltage $U_{\rm I} = U_{\rm in}$ is adjustable and automatically results in a voltage $U_{\rm O}=U_{\rm out}$. In the circuit (figure below), the resistors $R_1$ and $R_2$ can be changed.
The input resistance of the entire circuit $R_{\rm I}^0=\frac{U_{\rm I}}{I_{\rm I}}$ is easily obtained by considering the input side: since $\rm K1$ is at $0 ~\rm V$, $U_1 = U_\rm I$. The complete current flowing into the input passes through resistor $R_1$. So it is then true that the input resistance is $R_{\rm I} = R_1$. At the output resistance of the whole circuit $R_{\rm O}^0$, there is again a parallel connection between the output resistance of the operational amplifier $R_\rm O$ and the resistor $R_2$. So the output resistance will be slightly smaller than the output resistance of the operational amplifier $R_\rm O$.
Notice: Inverting Amplifier
In the case of the inverting amplifier:
- The input voltage $U_\rm I$ is at the inverting input of the operational amplifier.
- The feedback is done by a voltage divider of $R_1$ and $R_2$.
- The voltage gain is $A_{\rm V}= - \frac{R_2}{R_2}$ and is always less than or greater than 0. However, the magnitude of the voltage gain can be greater than or less than 1.
- The input resistance of the whole circuit is defined by $R_1$ and is usually smaller than the input resistance of the used (real) operational amplifier.
The output resistance is smaller than that of the used (real) operational amplifier.
Exercises
Exercise 3.3.1 Analysis of the impedance converter circuit with different operational amplifiers
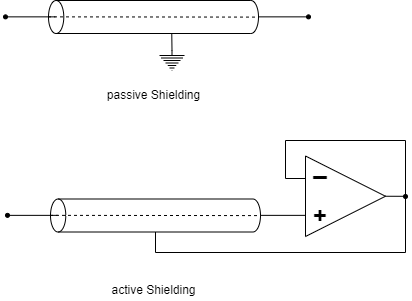
Imagine that you work in the company „HHN Mechatronics & Robotics“, which is a cheap mobile EKG – So you want to build a measuring device for the electrocardiogram or the cardiac voltage curve - for athletes and those in need. The measurement signal has only a few millivolts and microamps. In order to protect the signal from electromagnetic radiation on the way from the glued-on electrode to the evaluation electronics, a electromagnetic shielding placed around the line (see Abbildung 16, above). However, since this creates a parasitic capacitor, a colleague suggested active shielding. The shielding is always kept at the measuring voltage that is applied to the line via a voltage follower (see Abbildung 16, under). The parasitic capacitor is never charged due to this structure, since the same voltage prevails on both sides - there is no falsification of the signal. It is important for the application that the voltage follower reacts quickly.
You are supervised with the design of this voltage follower and should use the available operational amplifiers $\rm LM318$, $\rm uA741$, and $\rm uA776$ analyze in the voltage follower circuit.
Write a short report (problem description, circuit in TINA TI, results, discussion) and use TINA TI for the solution.
- Recreate the circuit described above for a realistic operational amplifier in Tina. Use a voltage generator as a source unit step with the amplitude $U_\rm A = 1.0 ~\rm V$.
- Simulate over
Analysis»Transient…the time course for the specified operational amplifiers.
Determine the time that elapses until the initial value of $0.1 ~\rm V$ for the first time $0.9 ~\rm V$ achieved ($10~\rm %$ to $90 ~\rm %$ of the amplitude, too. It is called rise time). - Describe the passage of time in each case. Are there any other differences besides the rise time?
- Based on the information provided, which of the three op amps would you choose for the problem?
In-depth information (not relevant to the exercise):
- Detailed description of a EMG/EKG Vorverstärkerschaltung
Exercise 3.3.2 Additional task to 3.3.1
In this exercise, the same question should be assumed as in exercise 3.3.1. This time, however, the influence of the impedance converter on the sensor signal is to be analyzed. The signal curve of the ECG voltage must be simulated by the voltage source. To do this, select Piecewise linear (3rd from the right) as the voltage source and use the curve below.
In addition, the influence on the current (= output resistor of the sensor) must be taken into account. To do this, insert a resistor with $20 ~\rm M\Omega$ directly in front of the non-inverting inputs.
- Now simulate the time course for $0 ~\rm s$ to $2 ~\rm s$ with „Use initial conditions“.
- What is the only difference in the output signals? (note y-axis)
- For a more realistic operational amplifier, 3 additional current sources and an additional voltage source must be taken into account in the equivalent circuit diagram (see Abbildung 17). In Tina, the values of these current sources can be viewed in the specifications of the simulated operational amplifier (double click on the OPV in
Circuit»Type…»Model Parameters). The analysis of the entire circuit (including the equivalent circuit diagram) is not to be considered here. It is assumed that the „input bias current“ of the operational amplifier is the decisive value.
Compare the values of the different operational amplifiers. - To simplify matters, think about the additional input voltage that results from the current of a single bias current source at the sensor resistor.
Excersie 3.3.3 Use of amplifiers in microcontrollers
In the Application Notes MTP3132 from the manufacturer Microchip, a block diagram is given on the 2nd page, which explains the use of the operational amplifier module of various PIC controllers.
- The logic input signal „$\rm UG$“ is shown in the block diagram. What happens in the logic circuit when it takes the value TRUE?
- Which operational amplifier circuit does this set?
- For what purpose is this adjusted op amp circuit used?
- The microcontroller PIC16F527 uses the explained op amp: in the microcontroller are 2 op amps $\rm OP1$ and $\rm OP2$. at which pin of the microcontroller can these be found?
Exercise 3.4.2 Input resistor of feedback systems
In chapter 3.4.2 the output resistance of the non-inverting amplifier was calculated. Determine the ratio between the input resistance in the same way $R_{\rm i,cl}$ a closed-loop amplifier circuit and the open-loop input resistance $R_{\rm i,ol}$.
Exercise 3.5.1 inverting amplifier
1. Derive the voltage gain $A_{\rm V}= {{U_{\rm O}}\over{U_{\rm I}}}$ for the inverting amplifier.
Use the procedure that was used for the non-inverting amplifier.
- What is looking for?
- Number of variables?
- Number of necessary equations?
- Establishing the known equations
- Derivation of the voltage gain
Take into account that for the differential gain $A_\rm D$ of the ideal OPV applies: $A_\rm D \rightarrow \infty$. And the following also applies: $1/A_\rm D \rightarrow 0$
But the following doesn't always apply: ${{C}\over{U_x \cdot A_\rm D}} \rightarrow 0$, for an unknown constant $C$ and a voltage $U_x$!
2. Which type of amplifier circuit (inverting or non-inverting amplifier) has the lower input resistance? Why?
Exercise 3.5.2. Variations of the non-inverting amplifier
Below you will find circuits with an ideal operational amplifier, which are similar to the non-inverting amplifier and whose voltage gain $A_V$ must be determined.
Assumptions
- $R_1 = R_3 = R_4 = R$
- $R_2 = 2 \cdot R$
- $U_\rm I$ comes from a low-resistance source
- $U_\rm O$ is due to a high-resistance consumer
Exercises
- Enter the voltage gain $A_\rm V$ for each circuit. A detailed calculation as before is not necessary.
- For Figure 7, indicate how the voltage gain can be determined.
- Generalize with the following justifications:
- How has a short circuit of the two OPV inputs must be taken into account?
- How do resistances have to be considered in the following cases:
- with one terminal (so „one connector“) directly and exclusively on an OPV input,
- with both terminals each directly connected to an OPV input.
- In which circuits do resistors $R_3$ and $R_4$ represent an unloaded voltage divider?
To approach the problems, you should try to use the knowledge from the inverting amplifier. It can be useful to simulate the circuits via Falstad-Circuit or Tina TI. In the first two circuits, tips can be seen under the illustration as support.
Important: As always in your studies, you should try to generalize the knowledge gained from the task.
Tipps
- How big is the current flow into the inverting and non-inverting input of an ideal operational amplifier? So what voltage drop would there be across a resistor whose one connection only leads to one input of the operational amplifier ($R_3$)?
- The operational amplifier always tries to output as much current at the output that the required minimum voltage $U_\rm D$ results between the inverting and non-inverting input. How high can $U_\rm D$ be assumed? Can this voltage also be built up via a resistor ($R_4$)?
- Can different resistors (e.g. because they are between the same nodes) be combined?
Abb. 1
Abb. 2
Abb. 3
Abb. 4
Abb. 5
Abb. 6
Abb. 7
Abb. 8
Abb. 9
Exercise 3.5.3. R-2R conductor
Abbildung 1
You work in the company „HHN Mechatronics & Robotics“, which is supposed to build a battery model for a customer. This model is intended to replicate a real battery. For this purpose, a voltage is to be output which is specified by a software model of the battery. A digital-to-analog converter (DAC) is therefore required.
You have found the DAC7741 for this. On page 12 of the datasheet you can see an image of the internal structure - this is similar to the illustration on the right. For an error analysis, you now want to understand this structure in more detail.
In the drawing on the right, the current switch position stands for 000b, so all switches $\rm SW1 … SW3$ are switched to ground. It is advisable to recreate the circuit in the Falstad-Circuit for a better understanding. In this case, it is advisable to measure the individual node voltages $\rm K1 … K3$ as well.
.
- $\rm SW_3$ = 1, $\rm SW_2$ = 0 and $\rm SW_1$ = 0 should now apply initially - that is, only switch $\rm SW_3$ is switched to $U_{\rm logic}$.
- To do this, draw the equivalent circuit diagram without a switch.
- Simplify this equivalent circuit using an equivalent resistor.
- The result is a resistance that lies between the inverting and non-inverting input. The operational amplifier always tries to feed so much current into the resistor network surrounding it that a small differential voltage $U_\rm D$ results. This is also possible with a (not too small) resistance between the inverting and non-inverting input.
So what is the gain?
- $\rm SW_3$ = 0, $\rm SW_2$ = 1 und $\rm SW_1$ = 0 should now apply initially - that is, only switch $\rm SW_3$ is switched to $U_{\rm logic}$.
- Here, too, draw the equivalent circuit diagram without a switch.
- Simplify this equivalent circuit using equivalent resistors.
- The statement about the above-mentioned resistance between the inverting and non-inverting input also applies here. You should also be aware of the voltage of node $\rm K_3$.
Now draw an equivalent circuit diagram of the left, taking the voltage at the node $\rm K_3$ of the ideal amplifier. - Now determine the voltage at node $\rm K_2$.
- This voltage at node $\rm K_2$ is the output voltage of an inverting amplifier, which starts from node $\rm K_2$ to the right. Now calculate the gain of the resulting network.
- The concept should be understood by now. Now specify which input / which switch specifies the LSB.
Exercise 3.5.4. Conversion of a unipolar signal into a bipolar signal
You work in the company „HHN Mechatronics & Robotics“ and are supposed to generate a bipolar signal ($-10 ~\rm V ... + 10 ~\rm V$) from a unipolar signal of a digital-to-analog converter ($0 ... 5 ~\rm V$) in a project. A colleague recommended the circuit shown on the right.
- First, analyze what change is made by pressing the switch $S$. How does the output signal change?
- Try to determine mathematically the relationship of $U_\rm O$ and $U_\rm I$ as $U_{\rm O}(U_{\rm I})$ by superposition.
- The circuit still has the problem that for a positive positive half-wave the output is still negative. Which additional circuit must be provided so that this problem can be solved?
Exercise 3.5.5. Linear Voltage Regulator
In order to get a constant (lower) voltage from a higher voltage input or a source with a broader spread of the voltage (e.g. a battery) often linear regulators are used. One example could be to get $5 ~\rm V$ from the car battery voltage (between $11 ~\rm V...14 ~\rm V$) for a microcontroller in a control unit e.g. the brake control unit. Linear regulator here means that a transistor as a variable resistor is used to drop the unwanted voltage.
Below, two types of such linear regulators are shown
- The first simulation shows a simple series regulator with a FET. „Series“ here marks the fact that the transistor is in series to the load resistor $R_\rm L$. The Zener diode $D$ has a current limiting series resistors $R_\rm D$ ahead. By the voltage divider of $R_\rm D$ and $D$, a relatively constant voltage will be created.
- The second simulation shows a more sophisticated circuit. Here, there is feedback from the output of the transistor back to the transistor controlling voltage. This feedback is given by $R1$, $R2$, and the operational amplifier.
Tasks
- In both simulations there are two sliders on the right-hand side:
- Input Voltage, which changes the ingoing voltage between $5~\rm V...20~\rm V$
- Load Resistance, which changes the load on the output between $10~\Omega...1~\rm k\Omega$
Play with these sliders and look for the differences! What are these? - The lower simulation with the operational amplifier is also called „Low DropOout“ (LDO). The dropout is the minimum voltage difference on the transistor. How can the terminology low dropoff can be explained?
- To which primitive OpAmp circuit does the LDO circuit ($R_1$, $R_2$ and OpAmp) look similar to?
How can the controlling of the transistor input voltage $U_{\rm GS}$ be explained? - Given a load resistor of $R_\rm L=1~\rm k\Omega$, an input voltage $U_\rm I=20~\rm V$, and an output voltage $U_\rm O=5~\rm V$, what is the dissipated power on the load and on the transistor?
Learning Questions
- Explain the difference between the unipolar and bipolar power supply of an OPV.
- Draw a sketch for bipolar and one for unipolar power supply.
- What are the advantages and disadvantages of unipolar and bipolar supply in OPV?
- What is the meaning of „virtual ground“? Under what circumstances is it found in opamp circuits?
- What are the golden rules in negative feedback amplifier circuits?
- What is the basic equation in negative feedback amplifier circuits?
- What are impedance transformers used for?
- How does the input voltage relate to the output voltage in an impedance converter and why?
- What does „voltage follower“ mean in the context of operational amplifiers and what are the characteristics of the voltage follower?
- References to the media used
-
Element License Link Abbildung 4: Image with internal operational amplifier (c) Microchip http://ww1.microchip.com/downloads/en/appnotes/90003132a.pdf