5 DC Circuit Transients (on RC elements)
- Capacitor in ICs --> MOSFET
- Charge/discharge FET capacitor.
Here we will shortly introduce the basic idea behind a capacitor. A more detailed analysis will follow in electrical engineering II.
A capacitor consists of two insulated conductors (electrodes) separated by an insulator (cf. figure 1).
The electrodes serve as “charge carrier storage”. This is done in the following manner:
- An external source draws charge carriers from one of the electrodes and carries them to the other electrode.
- If the external source is a voltage source with the voltage $U$, a stationary state is reached after a certain time.
In this state there is a fixed number of $+Q$ on the positive electrode and $-Q$ on the negative electrode. - These charges form an electric field in the space between the electrodes. This field stores the supplied energy.
As larger the voltage $U$, more charges $Q$ are stored on the electrode. This relationship is directly proportional to the proportionality constant $C$:
\begin{align*} C = {{Q}\over{U}} \quad \text{with:} \quad [C]=1 ~{\rm {As}\over{V}}= 1 ~{\rm F} = 1 ~\rm Farad \end{align*}
But it is not always directly recognizable that a structure contains a capacitor.
So the following examples are also capacitors:
- open switch: If there is a voltage between the two metal parts, charges can also accumulate there.
Since the distances are usually large and the air is used as the dielectric, the capacitance of the capacitor formed in this way is very small. - Overhead line: An overhead line also represents a capacitor against the ground potential of the earth. The charging and discharging by the alternating current leads to the fact that polarizable molecules can align themselves. For example, the water drops near the line are rolled through the field and hum with $100~\rm Hz$ and many times that (harmonics). Peak discharge results in a high-frequency crackle.
- Conductor trace: A trace on a PCB can also be a capacitor against a nearby ground plane. This can be a problem for digital signals (see the charge and discharge curves below).
- Human body: The human body can likewise pick up charge. The charge thus absorbed forms a capacitor with respect to other objects. This can be charged up to some $kV$. This is a particular problem in electrical laboratories, as the mere touching of components can destroy them.
- Membrane of nerve cells: Nerve cells also result in a capacitor due to the lipid bilayer (membrane of the nerve cell) and the two cellular fluids with different electrolytes (ions). The nerve cells are surrounded by a thick layer (myelin layer) for faster transmission. This lowers the capacitance and thus increases the successive charging of successive parts of the nerve cell. In diseases such as Creutzfeldt-Jakob or multiple sclerosis, this layer thins out. This leads to the delayed signal transmission which characterizes the disease patterns.
In the following, the charging process of a capacitor is to be considered in more detail. For this purpose, one has to realize, that during the charging of the capacitor, besides the voltage source $U_{\rm s}$ and the capacitor $C$, there is always a resistance $R$ in the circuit. This is composed of the internal resistance of the (non-ideal) voltage source, the internal resistance of the capacitor, and the parasitic (=interfering) resistance of the line. In practical applications, it is often desired that capacitors charge in a certain time range. For this purpose, another real resistor is inserted into the circuit. The resulting series of resistors and capacitors is called an RC element. It resembles a voltage divider in which a resistor has been replaced by a capacitor.
To start the charging, an (ideal) switch $S$ is inserted. The circuit to be considered then looks like shown in figure 2.
An ideal switch is characterized by:
- infinitely fast switching
- resistance of $0~\Omega$ in the closed state (“short circuit”)
- resistance $\rightarrow \infty$ in the open state (“open line”)
- no capacitive effect
- A time-varying voltage $u_C(t)$ across a capacitor or the voltage $U_{\rm s}$ of an ac voltage source as opposed to a constant voltage $U_{\rm s}$ across a constant voltage source.
- A time-varying current $i_L(t)$ across a coil or time-varying current $i_C(t)$ across a capacitor.
Since the time dependence is already clear from the lowercase letter, these quantities are occasionally not indicated by the trailing $(t)$. So it is $u = u(t)$.
5.1 Time Course of the Charging and Discharging Process
Learning Objectives
By the end of this section, you will be able to:
- know the time constant $\tau$ and in particularly calculate it.
- determine the time characteristic of the currents and voltages at the RC element for a given resistance and capacitance.
- know the continuity conditions of electrical quantities.
- know when (=according to which measure) the capacitor is considered to be fully charged/discharged, i.e. a steady state can be considered to have been reached.
In the simulation below you can see the circuit mentioned above in a slightly modified form:
- The capacitance $C$ can be charged via the resistor $R$ if the toggle switch $S$ connects the DC voltage source $U_{\rm s}$ to the two.
- But it is also possible to short-circuit the series circuit of $R$ and $C$ via the switch $S$.
- Furthermore, the current $i_C$ and the voltage $u_C$ are displayed in the oscilloscope as data points over time and in the circuit as numerical values.
- Additionally it is possible to change the capacitance value $C$ and resistance value $R$ with the sliders
Capacitance CandResistance R.
Exercises:
- Become familiar with how the capacitor current $i_C$ and capacitor voltage $u_C$ depend on the given capacitance $C$ and resistance $R$.
To do this, use for $R=\{ 10~\Omega, 100~\Omega, 1~k\Omega\}$ and $C=\{ 1~\rm µF, 10 ~ µF\}$. How fast does the capacitor voltage $u_C$ increase in each case n? - Which quantity ($i_C$ or $u_C$) is continuous here? Why must this one be continuous? Why must the other quantity be discontinuous?
In the following, this circuit is divided into two separate circuits, which consider only charging and only discharging.
Here is a short introduction about the transient behavior of an RC element (starting at 15:07 until 24:55)
To understand the charging process of a capacitor, an initially uncharged capacitor with capacitance $C$ is to be charged by a DC voltage source $U_{\rm s}$ via a resistor $R$.
- In order that the voltage $U_{\rm s}$ acts at a certain time $t_0 = 0 ~s$ the switch $S$ is closed at this time.
- Directly after the time $t_0$ the maximum current (“charging current”) flows in the circuit. This is only limited by the resistor $R$. The uncharged capacitor has a voltage $u_C(t_0)=0~V$ at that time. The maximum voltage $u_R(t_0)=U_{\rm s}$ is applied to the resistor. The current is $i_C(t_0)={{U_{\rm s}}\over{R}}$.
- The current causes charge carriers to flow from one electrode to the other. Thus the capacitor is charged and its voltage increases $u_C$.
- Thus the voltage $u_R$ across the resistor is reduced and so is the current $i_R$.
- With the current thus reduced, less charge flows on the capacitor.
- Ideally, the capacitor is not fully charged to the specified voltage $U_{\rm s}$ until $t \rightarrow \infty$. It then carries the charge: $q(t \rightarrow \infty) = Q = C \cdot U_{\rm s}$
The process is now to be summarized in detail in formulas. Linear components are used in the circuit, i.e. the component values for the resistor $R$ and the capacitance $C$ are independent of the current or the voltage. Then definition equations for the resistor $R$ and the capacitance $C$ are also valid for time-varying or infinitesimal quantities:
\begin{align*} R = {{u_R(t)}\over{i_R(t)}} = {{{\rm d}u_R}\over{{\rm d}i_R}} = {\rm const.} \\ C = {{q(t)} \over{u_C(t)}} = {{{\rm d}q} \over{{\rm d}u_C}} = {\rm const.} \tag{5.1.1} \end{align*}
The following explanations are also well explained in these two videos on charging and discharging.
Charging a capacitor at time t=0
By considering the loop, the general result is: the voltage of the source is equal to the sum of the two voltages across the resistor and capacitor.
\begin{align*} U_{\rm s} =u_R + u_C = R \cdot i_C + u_C \tag{5.1.2} \end{align*}
At the first instant ${\rm d}t$, an infinitesimally small charge “chunk” ${\rm d}q$ flows through the circuit driven by the current $i_C$ from the voltage source. For this, $(5.1.1)$ gives:
\begin{align*} i_C = {{{\rm d}q}\over{{\rm d}t}} \quad \text{and} \quad {\rm d}q = C \cdot {\rm d}u_C \end{align*}
The charging current $i_C$ can be determined from the two formulas:
\begin{align*} i_C = C \cdot {{{\rm d}u_C}\over{{\rm d}t}} \tag{5.1.3} \end{align*}
Thus $(5.1.2)$ becomes:
\begin{align*} U_{\rm s} &= u_R + u_C \\ &= R \cdot C \cdot {{{\rm d}u_C}\over{{\rm d}t}} + u_C \end{align*}
- here follows some mathematics:
-
This result represents a 1st order differential equation. This should generally be rewritten so that the part that depends (on the variable) is on one side and the rest is on the other. This is already present here. The appropriate approach to such a problem is:
\begin{align*} u_C(t) = \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \end{align*}
\begin{align*} U_{\rm s} &= R \cdot C \cdot {{\rm d}\over{{\rm d}t}}(\mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C}) + \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \\ &= R \cdot C \cdot \mathcal{AB} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \\ U_{\rm s} - \mathcal{C} &= ( R \cdot C \cdot \mathcal{AB} + \mathcal{A})\cdot {\rm e}^{\mathcal{B}\cdot t} \\ \end{align*}
This equation must hold for every $t$. This is only possible if the left, as well as the right term, become equal to 0.
Thus:\begin{align*} \mathcal{C} = U_{\rm s} \\ \\ R \cdot C \cdot \mathcal{AB} + \mathcal{A} &= 0 \quad \quad | : \mathcal{A} \quad | -1 \\ R \cdot C \cdot \mathcal{B} &= - 1 \\ \mathcal{B} &= - {{1}\over{R C}} \\ \end{align*}
So it follows:
\begin{align*} u_C(t) = \mathcal{A} \cdot {\rm e}^{\large{- {{t}\over{R C}} }} + U_{\rm s} \end{align*}
For the solution it must still hold that at time $t_0=0$ $u_C(t_0) = 0$ just holds:
\begin{align*} 0 &= \mathcal{A} \cdot {\rm e}^{\large{0}} + U_{\rm s} \\ 0 &= \mathcal{A} + U_{\rm s} \\ \mathcal{A} &= - U_{\rm s} \end{align*}
So the solution is:
\begin{align*} u_C(t) &= - U_{\rm s} \cdot {\rm e}^{\large{- {{t}\over{R C}}}} + U_{\rm s} \end{align*}
And this results in: \begin{align*} u_C(t) &= U_{\rm s} \cdot (1 - {\rm e}^{\large{- {{t}\over{R C}}}}) \end{align*}
And with $(5.1.3)$, $i_C$ becomes: \begin{align*} i_C(t) &= {{U_{\rm s}}\over{R}} \cdot {\rm e}^{\large{- {{t}\over{R C}} } } \end{align*}
In figure 4, the two time course diagrams for the charging voltage $u_C(t)$ and the charging current $i_C(t)$ of the capacitor are shown.
Notice:
- There must be a unitless term in the exponent. So $RC$ must also represent a time. This time is called time constant $\tau =R \cdot C$.
- At time $t=\tau$, we get: $u_C(t) = U_{\rm s} \cdot (1 - {\rm e}^{- 1}) = U_{\rm s} \cdot (1 - {{1}\over{\rm e}}) = U_{\rm s} \cdot ({{{\rm e}-1}\over{\rm e}}) = 0.63 \cdot U_{\rm s} = 63~\% \cdot U_{\rm s} $.
So, the capacitor is charged to $63~\%$ after one $\tau$. - At time $t=2 \cdot \tau$ we get: $u_C(t) = U_{\rm s} \cdot (1 - {\rm e}^{- 2}) = 86~\% \cdot U_{\rm s} = (63~\% + (100~\% - 63~\%) \cdot 63~\% ) \cdot U_{\rm s}$. So, after each additional $\tau$, the uncharged remainder ($1-63~\%$) is recharged to $63~\%$.
- After about $t=5 \cdot \tau$, the result is a capacitor charged to over $99~\%$. In real circuits, a charged capacitor can be assumed after $5 \cdot \tau$.
- The time constant $\tau$ can be determined graphically in several ways:
- Plotting the voltage value corresponding to $63~\%$ on the y-axis. Finding the point of intersection with the graph. Reading the time (see green lines in figure 4).
- Plotting the tangent to the (voltage) charge curve at the time of the discharged capacitor. This intersects a horizontal line at the level of the charging voltage at the point $t=\tau$ (see black and light blue lines in figure 4).
Discharging a capacitor at time t=0
The following situation is considered for the discharge:
- A capacitor charged to voltage $U_{\rm s}$ with capacitance $C$ is short-circuited across a resistor $R$ at time $t=t_0$.
- As a result, the full voltage $U_{\rm s}$ is initially applied to the resistor: $u_R(t_0)=U_{\rm s}$
- The initial discharge current is thus defined by the resistance: $i_C ={{u_R}\over{R}}$
- The discharging charges lower the voltage of the capacitor $u_C$, since: $u_C = {{q(t)}\over{C}}$
- Ideally, the capacitor is not fully discharged before $t \rightarrow \infty$.
Also, this process now is to put into a formula in detail. By looking at the loop, the general result is: the sum of the two voltages across the resistor and capacitor adds up to zero.
\begin{align*} 0 =u_R + u_C = R \cdot i_C + u_C \end{align*}
This gives $(5.1.3)$:
\begin{align*} 0 =u_R + u_C = R \cdot C \cdot {{{\rm d}u_C}\over{{\rm d}t}} + u_C \end{align*}
- also here uses some mathematics:
-
This result again represents a 1st order differential equation. The appropriate approach to such a problem is:
\begin{align*} u_C(t) = \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \end{align*}
\begin{align*} 0 &= R \cdot C \cdot {{\rm d}\over{{\rm d}t}}(\mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C}) + \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \\ &= R \cdot C \cdot \mathcal{AB} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{A} \cdot {\rm e}^{\mathcal{B}\cdot t} + \mathcal{C} \\ - \mathcal{C} &= ( R \cdot C \cdot \mathcal{AB} + \mathcal{A}) \cdot {\rm e}^{\mathcal{B}\cdot t} \\ \end{align*}
This equation must hold for every $t$. This is only possible if the left, as well as the right term, become equal to 0. Thus:
\begin{align*} \mathcal{C} = 0 \\ \\ R \cdot C \cdot \mathcal{AB} + \mathcal{A} &= 0 \quad \quad | : \mathcal{A} \quad | -1 \\ R \cdot C \cdot \mathcal{B} &= - 1 \\ \mathcal{B} &= - {{1}\over{R C}} \\ \end{align*}
So it follows:
\begin{align*} u_C(t) = \mathcal{A} \cdot {\rm e}^{\large{- {{t}\over{R C}} }} + 0 \end{align*}
For the solution it must still hold that at time $t_0=0$ $u_C(t_0) = U_{\rm s}$ just holds:
\begin{align*} U_{\rm s} &= \mathcal{A} \cdot {\rm e}^{\large{0}} \\ \mathcal{A} &= U_{\rm s} \end{align*}
Therefore, the result is:
\begin{align*} u_C(t) &= U_{\rm s} \cdot {\rm e}^{\large{- {{t}\over{R C}}}} \end{align*}
And this results in: \begin{align*} u_C(t) &= U_{\rm s} \cdot {\rm e}^{\large{- {{t}\over{\tau}}}} \quad \text{with} \quad \tau = R C \end{align*}
And with $(5.1.3)$, $i_C$ becomes: \begin{align*} i_C(t) &=- {{U_{\rm s}}\over{R}} \cdot {\rm e}^{\large{- {{t}\over{R C}} } } \end{align*}
In figure 6 the two time course diagrams are again shown; now for the discharge voltage $u_C(t)$ and the discharge current $i_C(t)$ of the capacitor. Since the current now flows out of the capacitor, the sign of $i_C$ is negative.
Periodic switching operations
In the simulation on the right, a periodic switching operation can be seen. The capacitor is periodically charged and discharged via the switch. Three sliders are given in the simulation to change the resistance $R$ (Resistance R), the capacity $C$ (Capacity C), and the frequency $f$ (Frequency f). In the simulation below, the voltage $u_C$ across the capacitor is shown in green and the current $i_C$ is shown in yellow.
Exercises:
- Increase the the frequency to $f=10~{\rm kHz}$ using the appropriate slider. What is the change for $u_C$ and $i_C$?
- Now increase the capacitance to $C=10 ~{\rm µF}$ using the corresponding slider. What is the change for $u_C$ and $i_C$?
- Now increase the resistance to $R= 1 ~\rm k\Omega$ using the corresponding slider. What is the change for $u_C$ and $i_C$?
5.2 Energy stored in a Capacitor
Learning Objectives
By the end of this section, you will be able to:
- calculate the energy content in a capacitor.
- calculate the change in energy of a capacitor resulting from a change in voltage between the capacitor terminals.
- calculate (initial) current, (final) voltage, and charge when balancing the charge of several capacitors (also via resistors).
Now the capacitor as energy storage is to be looked at more closely. This derivation is also explained in this youtube video. For this, we consider again the circuit in figure 2 an. According to the chapter Preparation, Properties, and Proportions, the power for constant values (DC) is defined as:
\begin{align*} P={{\Delta W}\over{\Delta t}} = U \cdot I \end{align*}
For variable signals, the instantaneous power is given as:
\begin{align*} p={{{\rm d}w}\over{{\rm d}t}} = u \cdot i \end{align*}
Energy consideration of the capacitor
Charging the capacitor at time $t_0 = 0$ results in $\Delta W = \Delta W_C$ for the stored energy at a later time $t_1 =t$:
\begin{align*} \Delta W_C = \int_{t_0}^{t_1} {\rm d}w = \int_{0}^t u \cdot i \cdot {\rm d}t = \int_{0}^t u_C \cdot i_C {\rm d}t \tag{5.2.1} \end{align*}
During the charging process \begin{align*} u_C(t) = U_{\rm s} \cdot (1 - {\rm e}^{ -{{t}\over{\tau}} }) \\ i_C(t) = {{U_{\rm s}}\over{R}} \cdot {\rm e}^{ -{{t}\over{\tau}} } \tag{5.2.2} \end{align*}
In particular:
\begin{align*} C = {{q(t)}\over{u_C(t)}} \quad &\rightarrow \quad &q(t) &= {u_C(t)}\cdot{C} \\ i_C(t) = {{{\rm d} q(t)}\over{{\rm d}t}} \quad &\xrightarrow{C=\rm const.} \quad &i_C(t) &= C \cdot {{{\rm d} u_C(t)}\over{{\rm d}t}} \end{align*}
Thus, the stored energy from formula $(5.2.1)$:
\begin{align*} \Delta W_C &= \int_{0}^t u_C(t) \cdot C \cdot {{{\rm d} u_C(t)}\over{{\rm d}t}} {\rm d}t \quad & | \text{ substitution of integration variable: } t \rightarrow u_C\\ &= \int_{U_0}^{U_1} u_C(t) \cdot C \cdot {\rm d}u_C \quad & | \text{ Since the capacity is constant, it can be written ahead of the integral}\\ &= C \cdot \int_{U_0}^{U_1} u_C \, {\rm d} u_C \\ &= C \cdot \left[{{1}\over{2}} u_C^2 \right] _{U_0}^{U_1} \\ \end{align*} \begin{align*} \boxed{\Delta W_C= {{1}\over{2}} C \cdot (U_1^2-U_0^2)} \tag{5.2.3} \end{align*}
Thus, for a fully discharged capacitor ($U_{\rm s}=0~{\rm V}$), the energy stored when charging to voltage $U_{\rm s}$ is $\Delta W_C={{1}\over{2}} C \cdot U_{\rm s}^2$.
Energy Consideration on the Resistor
The converted energy can also be determined for the resistor:
\begin{align*} \Delta W_R = \int_{0}^t u_R \cdot i_R {\rm d}t = \int_{0}^t R \cdot i_R \cdot i_R {\rm d}t = R \cdot \int_{0}^t i_R^2 {\rm d}t \end{align*}
Since the current through the capacitor $i_C$ is equal to that through the resistor $i_R$, it follows via $(5.2.2)$:
\begin{align*} \Delta W_R &= R \cdot \int_{0}^t \left( { {U_{\rm s}}\over{R}} \cdot {\rm e}^ { -{{t}\over{\tau}}} \right)^2 {\rm d}t \\ &= { {U_{\rm s}^2}\over{R}} \cdot \int_{0}^t {\rm e}^ { -{{2 \cdot t}\over{\tau}}} {\rm d}t \\ &= { {U_{\rm s}^2}\over{R}} \cdot \left[ -{{\tau }\over{2}} \cdot {\rm e}^ { -{{2 \cdot t}\over{\tau}}} \right]_{0}^t \quad & | \text{with } \tau = R \cdot C \\ &= -{{1}\over{2}} \cdot { U_{\rm s}^2}\cdot{C} \cdot \left[ {\rm e}^ { -{{2 \cdot t}\over{\tau}}} \right]_{0}^t \\ \end{align*}
For $t \rightarrow \infty$ we get:
\begin{align*} \Delta W_R &= -{{1}\over{2}} \cdot {U_{\rm s}^2}\cdot{C} \cdot \left[ {\rm e}^ { -{{2 \cdot t}\over{\tau}}} \right]_{0}^{\infty} \\ &= -{{1}\over{2}} \cdot {U_{\rm s}^2}\cdot{C} \cdot \left[ 0 - 1 \right] \\ \end{align*} \begin{align*} \boxed{ \Delta W_R = {{1}\over{2}} \cdot {U_{\rm s}^2}\cdot{C}} \tag{5.2.4} \end{align*}
This means that the energy converted at the resistor is independent of the resistance value (for an ideal constant voltage source $U_{\rm s}$ and given capacitor $C$)! At first, this doesn't really sound comprehensible. No matter if there is a very large resistor $R_1$ or a tiny small resistor $R_2$: The same waste heat is always produced. Graphically, this apparent contradiction can be resolved like this: A higher resistor $R_2$ slows down the small charge packets $\Delta q_1$, $\Delta q_2$, … $\Delta q_n$ more strongly. But a considered single charge packet $\Delta q_k$ will nevertheless pass the same voltage across the resistor $R_1$ or $R_2$ since this is given only by the accumulated packets in the capacitor: $u_r = U_{\rm s} - u_C = U_{\rm s} - {{q}\over{C}}$.
In real applications, as mentioned in previous chapters, ideal voltage sources are not possible. Thus, without a real resistor, the waste heat is dissipated proportionally to the internal resistance of the source and the internal resistance of the capacitor. The internal resistance of the capacitor depends on the frequency but is usually smaller than the internal resistance of the source.
Consideration of total energy turnover
In the previous considerations, the energy conversion during the complete charging process was also considered. It was found that the capacitor stores the energy $W_C= {{1}\over{2}} \cdot {U_{\rm s}^2}\cdot{C} $ (see $(5.2.3)$) and at the resistor the energy $W_R= {{1}\over{2}} \cdot {U_{\rm s}^2}\cdot{C} $ (see $(5.2.4)$) into heat. So, in total, the voltage source injects the following energy:
\begin{align*} \Delta W_0 &=\Delta W_R + \Delta W_C = {U_{\rm s}^2}\cdot{C} \end{align*}
This also follows via $(5.2.1)$:
\begin{align*} \Delta W_0 &= \int_{0}^{\infty} u_0 \cdot i_0 \cdot {\rm d}t \quad | \quad u_0 = U_{\rm s} \text{ is constant because constant voltage source!} \\ &= U_{\rm s} \cdot \int_{0}^{\infty} i_C {\rm d}t \\ &= U_{\rm s} \cdot \int_{0}^{\infty} {{{\rm d}q}\over{{\rm d}t}} {\rm d}t \\ &= U_{\rm s} \cdot \int_{0}^Q {\rm d}q = U_{\rm s} \cdot Q \quad | \quad \text{where } Q= C \cdot U_{\rm s} \\ &= U_{\rm s}^2 \cdot C \\ \end{align*}
This means that only half of the energy emitted by the source is stored in the capacitor! Again, This doesn't really sound comprehensible at first. And again, it helps to look at small packets of charge that have to be transferred from the ideal source to the capacitor. figure 8 shows current and voltage waveforms across the capacitor and the stored energy for different resistance values. There, too, it can be seen that the maximum stored energy (dashed line in the figure at right) is given by $\Delta W= {{1}\over{2}} {U_{\rm s}^2}\cdot{C} $ alone. $U_{\rm s}^2 \cdot C = {{1}\over{2}} \cdot (5~{\rm V})^2 \cdot 1 ~{\rm µF} = 12.5 ~{\rm µWs}$ is given.
This can also be tested in the following simulation. In addition to the RC element shown so far, a power meter and an integrator are also drawn here. It is possible to display the instantaneous power and the stored energy. Via the slider Resistance R the resistance value can be varied. The following values are shown in the oscilloscopes:
- left: Current $u_C$ and voltage $i_C$ at the capacitor.
- middle: Instantaneous power $p_C = u_C \cdot i_C$ of the capacitor.
- right: stored energy $w_C = \int u_C \cdot i_C \; {\rm d}t$ of the capacitor
Exercises
Exercise 5.2.1 Capacitor charging/discharging practice Exercise
Exercise E 5.2.2 Capacitor charging/discharging
The following circuit shows a charging/discharging circuit for a capacitor.
The values of the components shall be the following:
- $R_1 = 1.0 \rm k\Omega$
- $R_2 = 2.0 \rm k\Omega$
- $R_3 = 3.0 \rm k\Omega$
- $C = 1 \rm \mu F$
- $S_1$ and $S_2$ are opened in the beginning (open-circuit)
1. For the first tasks, the switch $S_1$ gets closed at $t=t_0 = 0s$.
1.1 What is the value of the time constant $\tau_1$?
The time constant $\tau$ is generally given as: $\tau= R\cdot C$.
Now, we try to determine which $R$ and $C$ must be used here.
To find this out, we have to look at the circuit when $S_1$ gets closed.
We see that for the time constant, we need to use $R=R_1 + R_2$.
1.2 What is the formula for the voltage $u_{R2}$ over the resistor $R_2$? Derive a general formula without using component values!
To get a general formula, we again look at the circuit, but this time with the voltage arrows.
We see, that: $U_1 = u_C + u_{R2}$ and there is only one current in the loop: $i = i_C = i_{R2}$
The current is generally given with the exponential function: $i_c = {{U}\over{R}}\cdot e^{-t/\tau}$, with $R$ given here as $R = R_1 + R_2$.
Therefore, $u_{R2}$ can be written as:
\begin{align*} u_{R2} &= R_2 \cdot i_{R2} \\ &= U_1 \cdot {{R_2}\over{R_1 + R_2}} \cdot e^{-t/ \tau} \end{align*}
2. At a distinct time $t_1$, the voltage $u_C$ is charged up to $4/5 \cdot U_1$.
At this point, the switch $S_1$ will be opened.
Calculate $t_1$!
We can derive $u_{C}$ based on the exponential function: $u_C(t) = U_1 \cdot (1-e^{-t/\tau})$.
Therefore, we get $t_1$ by:
\begin{align*} u_C = 4/5 \cdot U_1 &= U_1 \cdot (1-e^{-t/\tau}) \\ 4/5 &= 1-e^{-t/\tau} \\ e^{-t/\tau} &= 1-4/5 = 1/5\\ -t/\tau &= \rm ln (1/5) \\ t &= -\tau \cdot \rm ln (1/5) \\ \end{align*}
3. The switch $S_2$ will get closed at the moment $t_2 = 10 ~\rm ms$. The values of the voltage sources are now: $U_1 = 5.0 ~\rm V$ and $U_2 = 10 ~\rm V$.
3.1 What is the new time constant $\tau_2$?
Again, the time constant $\tau$ is given as: $\tau= R\cdot C$.
Again, we try to determine which $R$ and $C$ must be used here.
To find this out, we have to look at the circuit when $S_1$ is open and $S_2$ is closed.
We see that for the time constant, we now need to use $R=R_3 + R_2$.
\begin{align*} \tau_2 &= R\cdot C \\ &= (R_3 + R_2) \cdot C \\ \end{align*}
3.2 Calculate the moment $t_3$ when $u_{R2}$ is smaller than $1/10 \cdot U_2$.
To calculate the moment $t_3$ when $u_{R2}$ is smaller than $1/10 \cdot U_2$, we first have to find out the value of $u_{R2}(t_2 = 10 ~\rm ms)$, when $S_2$ just got closed.
- Starting from $t_2 = 10 ~\rm ms$, the voltage source $U_2$ charges up the capacitor $C$ further.
- Before at $t_1$, when $S_1$ got opened, the value of $u_c$ was: $u_c(t_1) = 4/5 \cdot U_1 = 4 ~\rm V$.
- This is also true for $t_2$, since between $t_1$ and $t_2$ the charge on $C$ does not change: $u_c(t_2) = 4 ~\rm V$.
- In the first moment after closing $S_2$ at $t_2$, the voltage drop on $R_3 + R_2$ is: $U_{R3+R2} = U_2 - u_c(t_2) = 6 ~\rm V$.
- So the voltage divider of $R_3 + R_2$ lead to $ \boldsymbol{u_{R2}(t_2 = 10 ~\rm ms)} = {{R_2}\over{R_3 + R2}} \cdot U_{R3+R2} = {{2 {~\rm k\Omega}}\over{3 {~\rm k\Omega} + 2 {~\rm k\Omega} }} \cdot 6 ~\rm V = \boldsymbol{2.4 ~\rm V} $
We see that the voltage on $R_2$ has to decrease from $2.4 ~\rm V $ to $1/10 \cdot U_2 = 1 ~\rm V$.
To calculate this, there are multiple ways. In the following, one shall be retraced:
- We know, that the current $i_C = i_{R2}$ subsides exponentially: $i_{R2}(t) = I_{R2~ 0} \cdot {\rm e}^{-t/\tau}$
- So we can rearrange the task to focus on the change in current instead of the voltage.
- The exponential decay is true regardless of where it starts.
So from ${{i_{R2}(t)}\over{I_{R2~ 0}}} = {\rm e}^{-t/\tau}$ we get \begin{align*} {{i_{R2}(t_3)}\over{i_{R2}(t_2)}} &= {\rm exp} \left( -{{t_3 - t_2}\over{\tau_2}} \right) \\ -{{t_3 - t_2}\over{\tau_2}} &= {\rm ln } \left( {{i_{R2}(t_3)}\over{i_{R2}(t_2)}} \right) \\ t_3 &= t_2 - \tau_2 \cdot {\rm ln } \left( {{i_{R2}(t_3)}\over{i_{R2}(t_2)}} \right) \\ t_3 &= 10 ~{\rm ms} - 5~{\rm ms} \cdot {\rm ln } \left( {{1 ~\rm V }\over{2.4 ~\rm V }} \right) \\ \end{align*}
3.3 Draw the course of time of the voltage $u_C(t)$ over the capacitor.
Exercise 5.2.3: Charging and Discharging of RC elements (exam task, ca. 11 % of a 60-minute exam, WS2020)
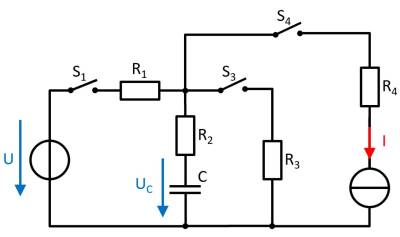
The circuit shown right is given with the following data:
- $U = 10 ~{\rm V}$
- $I = 4 ~{\rm mA}$
- $R_1 = 100 ~\Omega, R_2 = 80 ~\Omega, R_3 = 50 ~\Omega, R_4 = 10 ~\Omega$
- $C = 40 ~{\rm nF}$
At first, the voltage drop on the capacitor $u_C = 0$, and all switches are open. The switch S1 will be closed at $t = 0$.
1. Determine the time constant $\tau$ for this charging process.
- What equivalent circuit can be found for the mentioned states of the switches?
- What parameter do you need to determine $\tau$?
- The charging current is flown through which component?
2. What is the value of the voltage $u_C(t)$ drop over the capacitor $C$ at $t=10 ~{\rm µs}$?
3. What is the value of the stored energy in the capacitor, when it is fully charged?
4. Determine the new time constant when the switch $S_1$ will be opened and the switch $S_3$ will be closed simultaneously.
5. When the capacitor is completely discharged, all switches will be opened. The switch $S_4$ will be closed at $t= 0$.
What is the voltage $u_C$ at the capacitor C after $t = 1 ~ {\rm µs}$?
- Through the current source there is a continuous flow of electric charge into the capacitor.
- The resistors passed by the current on the way to the capacitor are irrelevant. They only increase the voltage of an ideal current source to guarantee the current.
Exercise E5.2.4 Charge balance of two capacitors
(educational exercise, not part of an exam)
In the simulation, you see the two capacitors $C_1$ and $C_2$ (The two small resistors with $1 ~\rm µ\Omega$ have to be there for the simulation to run). At the beginning, $C_1$ is charged to $10~{\rm V}$ and $C_2$ to $0~{\rm V}$. With the switches $S_1$ and $S_2$ you can choose whether
- the capacitances $C_1$ and $C_2$ are shorted, or
- the capacitors $C_1$ and $C_2$ are connected via resistor $R$.
On the right side of the simulation, there are some additional “measuring devices” to calculate the stored potential energy from the voltages across the capacitors.
In the following, the charging and discharging of a capacitor are to be explained with this construction.
Under the electrical structure, the following quantities are shown over time:
| Voltage $u_1(C_1)$ of the first capacitor | Voltage $u_2(C_2)$ of the second capacitor | Stored energy $w_1(C_1)$ | Stored energy $w_2(C_2)$ | Total energy $\sum w$ |
|---|---|---|---|---|
| Initially charged to $10~{\rm V}$ | Initially neutrally charged ($0~{\rm V}$) | Initially holds: $w_1(C_1)= {1 \over 2} \cdot C \cdot U^2 = {1 \over 2} \cdot 10~{\rm µF} \cdot (10~{\rm V})^2 = 500~{\rm µW}$ In the oscilloscope, equals $1~{\rm V} \sim 1~{\rm W}$ | Initially, $w_2(C_2)=0$ , since the capacitor is not charged. | The total energy is $w_1 + w_2 = w_1$ |
The capacitor $C_1$ has thus initially stored the full energy and via closing of the switch, $S_2$ one would expect a balancing of the voltages and an equal distribution of the energy $w_1 + w_2 = 500~\rm µW$.
- Close the switch $S_2$ (the toggle switch $S_1$ should point to the switch $S_2$). What do you find?
- What do the voltages $u_1$ and $u_2$ do?
- What are the energies and the total energy?
How is this understandable with the previous total energy?
- Open $S_2$ - the changeover switch $S_1$ should not be changed. What do you find?
- What do the voltages $u_1$ and $u_2$ do?
- What are the energies and the total energy?
How is this understandable with the previous total energy?
- Repeat 1. and 2. several times. Can anything be deduced regarding the distribution of energy?
- Change the switch $S_2$ to the resistor. What do you observe?
- What do the voltages $u_1$ and $u_2$ do?
- What are the energies and the total energy?
How is this understandable with the previous total energy?