Dies ist eine alte Version des Dokuments!
5 Filterschaltungen
- Auch für die Grundschaltungen II ist sind die Operationsverstärker-Grundschaltungen auf Microcontroller.net zu empfehlen
- Lehr- und Arbeitsbuch Operationsverstärker (Joachim Federau) (über das Hochschulnetz einsehbar)
Einführendes Beispiel
Bei verschiedenen Anwendungen in harscher Umgebung (z.B. Sensoren im Motorraum oder in industirelle Umgebung, Kommunikation mit Satelliten) werden aus den klaren digitalen Sendesignalen verrauschte Signale am Empfänger. In der Simulation rechts zeigt das linke Oszilloskopbild das ursprüngliche Signal. Im zweiten Oszilloskopbild ist das verrauschte Signal zu sehen.
Eine Möglichkeit solche Signale aufzuarbeiten, ist die Verwendung von Filtern. Filter wurden auch bereits im Fach Elektrotechnik 2 beschrieben. Die klassischen $R C$-Filter sind dabei passiv. Das bedeutet, dass der Spannungswert zwar gefiltert wird, aber der Ausgangsstrom des Filters immer geringer ist als der am Eingang gemessene Strom. Um eine bessere Filterung und nachträgliche Nutzung des Signals zu ermöglichen, können aktive Filter eingesetzt werden. Diese können durch Operationsverstärker aufgebaut werden.
In der Simulation sind zwei Tiefpass-Filter dargestellt. Diese dämpfen die hochfrequenten Anteile im Signal ab. Das Signal $U_{A1}$ nach der ersten Filterstufe zeigt bereits deutlich weniger Rauschen. Im Signal $U_{A2}$ ist noch ein geringeres Rauschen sichtbar, aber auch die ansteigende und abfallende Flanke wird nicht mehr scharf dargestellt.
Mit dem Schalter (links in der Simulation) kann ein frequenz-veränderliches Testsignal (Sweep) eingespeist werden. Dieses zeigt deutlich, dass der Filter aus hochfrequenten Schwingungen am Eingang eine kleinere Amplitude am Filterausgang erzeugt.
In diesem Kapitel sollen die Grundlagen für aktive Hoch- und Tiefpassfilter aus Operationsverstärker erklärt werden.
Ziele für Grundschaltungen II
Nach dieser Lektion sollten Sie:
- das Superpostitionsverfahren auf Operationsverstärkerschaltungen anwenden können.
- wissen, worin sich Differenzverstärker und Instrumentenverstärker unterscheiden (Schaltung, Anwendungen, Vor- und Nachteile).
- wissen, wie die Schaltung und Übertragungsfunktion eines Spannungs-Strom-Wandler und Strom-Spannungs-Wandler aussieht.
- Anwendungen für den Umkehraddierer, Spannungs-Strom-Wandler und Strom-Spannungs-Wandler nennen können.
5.0 Darstellung von Zahlenwerten
Damit Filterschaltungen analysiert werden können, sollen vorher verschiedene Möglichkeiten zum Darstellen der Zahlenwerte erklärt werden.
5.0.1 Das dB-Maß
Das Dezibel-Maß ist eine Hilfmaßeinheit, welche die Handhabung mit Verhältnissen (z.B. $U_2/U_1$) erleichtert. Diese Verhältnisse werden in der Technik Pegel genannt. Der Pegel ermöglicht den Bezug auf ein Referenzgröße. In der elektronischen Schaltungstechnik wird das Dezibel als dimensionslose Einheit für Strom- bzw. Spannungsverhältnisse genutzt. Dies wird zukünftig insbesondere für die Verstärkung $A_V = \frac{U_A}{U_E}$ und Faktoren interessant.
Die Umrechnung in einen Pegel in $dB$ ist für Strom- bzw. Spannungsverhältnisse über folgende Gleichung definiert:
$\boxed{A_V^{dB}=20 dB \cdot log_{10}\left(\frac{U_2}{U_1}\right)=20 dB \cdot log_{10}A_V}$ bzw. $A_C^{dB}=20 dB \cdot log_{10}\left(\frac{I_2}{I_1}\right)$
technische Pegel in dB
| Name | Symbol | Formel | Referenzgröße für 0dB |
|---|---|---|---|
| Spannungspegel | $dBV$ | $20 \cdot log_{10}(V/V_{ref})$ | $0dBV \widehat{=} 1V$ |
| Leistungspegel | $dBm$ | $10 \cdot log_{10}(P/P_{ref})$ | $0dBV \widehat{=} 1mW$ |
| Leistungspegel | $dBW$ | $10 \cdot log_{10}(P/P_{ref})$ | $0dBV \widehat{=} 1W$ |
| Schalldruckpegel | $dBA$ | $20 \cdot log_{10}(p/p_{ref})$ | $0dBV \widehat{=} 20\mu Pa$ |
Zu beachten ist, dass das diese Gleichung für Leistungsgrößen, also Verhältnisse von $P$ sich etwas ändert. Wird $P \sim U^2$ bzw. $U \sim P^\frac{1}{2}$ berücksichtigt, dann ergibt sich:
$A_P^{dB}=20 dB \cdot log_{10}\left(\frac{P_2^\frac{1}{2}}{P_1^\frac{1}{2}}\right)$
$ =\color{blue}{20 dB \cdot \frac{1}{2}} \cdot log_{10}\left(\frac{P_2}{P_1}\right) =\color{blue}{10 dB} \cdot log_{10}\left(\frac{P_2}{P_1}\right) $
Rechts in der Tabelle sind verschiedene, in der Technik häufig genutzte Pegel zu finden. Im Folgenden wird nur der Spannungspegel genutzt und mit dem Symbol $dB$ angegeben.
einfache Beispiele von Spannungspegel in dB
| linearer Faktor | Pegel [$dB$] |
|---|---|
| $0,01$ | $-40dB$ |
| $0,1$ | $-20dB$ |
| $1$ | $0dB$ |
| $2$ | $\approx 6dB$ |
| $10$ | $20dB$ |
| $100$ | $40dB$ |
Durch diese Gleichung lassen sich verschiedene lineare Faktoren und Verhältnisse $A = \boxed{}_2 / \boxed{}_1$ in einen Pegel $A^{dB}$ in $dB$ umwandeln. Gelegentlich wird im Folgenden der hochgestellte Index $\boxed{}^{dB}$ weggelassen; in diesem Fall ist der Pegel durch die Einheit nach dem Zahlenwert gekennzeichnet.
Beispiele:
- Für $A_V= \color{green}{1} $ ergibt sich $ A_V^{dB}(\color{green}{1}) = 20 dB \cdot \underbrace{log_{10}\left(\color{green}{1}\right)}_\color{blue}{x} \qquad \qquad \qquad \rightarrow \boldsymbol{A_V^{dB}(\color{green}{1})} \quad = 20 dB \cdot 0 \quad \ \boldsymbol{= 0 dB}$
Hierbei hat $\color{blue}{x}$ den Wert, der $10^\color{blue}{x} = \color{green}{1}$ ergibt, also gerade $\color{blue}{x}=0$.
- Für $A_V= \color{green}{0,01} $ ergibt sich $ A_V^{dB}(\color{green}{0,01}) = 20 dB \cdot \underbrace{log_{10}\left(\color{green}{0,01}\right)}_\color{blue}{x} \qquad \rightarrow \boldsymbol{A_V^{dB}(\color{green}{0,01})} = 20 dB \cdot (-2) \boldsymbol{= -40 dB}$
Hierbei hat $\color{blue}{x}$ den Wert, der $10^\color{blue}{x} = \color{green}{0,01}$ ergibt, also gerade $\color{blue}{x}=-2$.
- Für $A_V= \color{green}{2} $ ergibt sich $ A_V^{dB}(\color{green}{2}) = 20 dB \cdot \underbrace{log_{10}\left(\color{green}{2}\right)}_\color{blue}{x} \qquad \qquad \qquad \rightarrow \boldsymbol{A_V^{dB}(\color{green}{2})} \quad\approx 20 dB \cdot 0,30103 \boldsymbol{\approx 6 dB}$
Hierbei hat $\color{blue}{x}$ den Wert, der $10^\color{blue}{x} = \color{green}{2}$ ergibt. So entspricht $\color{blue}{x}\approx 0,30103$.
Verwendung des dB-Maß
Das Dezibel bietet einige Vorteile, welche bei den im folgenden betrachteten Filter-Elementen Verwendung finden:
- handlichere Zahlenwerte: Werden sehr große oder sehr kleine lineare Werte benötigt, so hat die Zahl des sich ergebenden Pegel weniger Stellen. Beispiel: $A_V = 10000000 \rightarrow A_V^{dB}= 140dB$. Dadurch ergibt sich auch weniger „Nullen-Zählen“.
- Bezug zu Sinnesempfindungen: Sinnesempfindungen wie Helligkeit und Lautstärke wirken nahezu exponentiell. Das bedeutet jede Verzehnfachung der zugrunde liegenden physikalischen Größe (Photonenanzahl oder Schalldruck) wirkt nicht zehnmal so stark, sondern scheint einen additiven Effekt zu haben.
- leichteres Rechnen: Durch den Logarithmus in der Definitionsgleichung wird aus jeder Multiplikation von linearen Faktoren eine Addition von Pegeln:
$A_V^{dB}(A_1 \cdot A_2) = 20dB \cdot log_{10}(A_1 \cdot A_2) = 20dB \cdot log_{10}(x_1) + 20dB \cdot log_{10}(x_2) = A_V^{dB}(A_1) + A_V^{dB}(A_2) $
Gerade der letzte Punkt der Rechnung soll nochmal betrachtet werden. In Abbildung 1 sind mehrere hintereinander geschalteten Verstärker zu mit beispielhaften Spannungsverstärkungswerten sehen.
Die Gesamtverstärkung ergibt sich hier aus dem Produkt der Einzelverstärkungen: $A_{V,ges}=\prod A_i = A_1 \cdot A_2 \cdot A_3$.
Die Ermittlung der Gesamtverstärkung war vor Zeiten des Taschenrechners durch die Multiplikationen eher aufwändig. Für die Pegel ergibt sich eine Addition: $A_{V,ges}^{dB}=\sum A_i^{dB} = A_1^{dB} + A_2^{dB} + A_3^{dB}$.
Hier wäre dies: $A_{V,ges}^{dB}=\sum A^{dB} = 88dB + (-58dB) + 14dB = 44dB$
Merke: dB-Maß
Für Strom und Spannungspegel gilt:
- Ein linearer Faktor von $\color{green}{\times 10}$ ergibt im Pegel $+ 20dB$
- Ein linearer Faktor von $\color{green}{\times 2}$ ergibt im Pegel $+ 6dB$
- Der linearer Wert $A_V = 1$ entspricht $0 dB$
Bei hintereinander geschalteten Systemen ist für die Ermittlung der Verstärkung
- das lineare Maß $A_V$ zu multiplizieren und
- der Pegel $A_V^{dB}$ zu addieren.
schwierigere Beispiele von Spannungspegel in dB
Mit diesen Kenntnissen lassen sich über die Stützstellen $\color{green}{\times 10} \rightarrow + 20dB$ und $\color{green}{\times 2} \rightarrow + 6dB$ ohne Taschenrechner leicht aus einem Pegel in $dB$ die linearen Werte ermitteln.
Beispiele:
- $A_V^{dB}=58dB$
mit Stützstellen: $A_V^{dB}=58dB = 40dB + 18dB = \color{blue}{2}\cdot 20dB + \color{magenta}{3}\cdot 6dB$
Das wird linear zu $ \qquad \qquad \qquad \qquad \qquad \ A_V = 10^\color{blue}{2} \qquad \cdot \qquad 2^\color{magenta}{3} \qquad = 100 \cdot 8 = 800$
- $A_V^{dB}=56dB$
mit Stützstellen: $A_V^{dB}=56dB = 60dB - 24dB = \color{blue}{4}\cdot 20dB + \color{magenta}{-4}\cdot 6dB$
Das wird linear zu $ \qquad \qquad \qquad \qquad \qquad \ A_V = 10^\color{blue}{4} \qquad \cdot \qquad 2^\color{magenta}{-4} \qquad = 10000 \cdot \frac{1}{16} = 625$
oder $A_V = 20dB + 36dB = 10^\color{blue}{1} \cdot 2^\color{magenta}{6} = 10 \cdot 64 = 640$
- $A_V^{dB}=55dB$
mit Stützstellen: $A_V^{dB}=56dB = 40dB + 18dB - 3dB = \color{blue}{2}\cdot 20dB + \color{magenta}{3}\cdot 6dB + \color{teal}{-\frac{1}{2}}\cdot 6dB$
Das wird linear zu $ \qquad \qquad \qquad \qquad \qquad \qquad \ A_V = 10^\color{blue}{2} \qquad \cdot \qquad 2^\color{magenta}{3} \qquad \cdot \qquad 2^\color{teal}{-\frac{1}{2}} \approx 100 \cdot 8 \cdot 0,707 = 560$
Der Wert $-3dB$ wird im Folgenden noch genutzt werden.
5.0.2 Das Bode-Diagramm
Ziel des Bodediagramms ist es das Übertragungsverhalten von Systemen übersichtlich und deutlich darzustellen.
Vorbetrachtung: Komplexe Zahlen
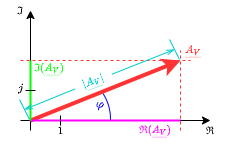
Eine komplexe Zahl kann stets auf zwei reelle Zahlenwerte reduziert werden. Für die genaue Definition dieser Zahlenwerte gibt es verschiedene Möglichkeiten (Abbildung 2):
- Definition über Realteil $\Re(\underline{A}_V)=A_V \cdot cos(\varphi)$ und Imaginärteil $\Im(\underline{A}_V)=A_V \cdot sin(\varphi)$
- Definition über Betrag $A_V = |\underline{A}_V|$ und Phase $\varphi = arctan \left( \frac{\Im(\underline{A}_V)}{\Re(\underline{A}_V)} \right)$
Die 2. Definition ist bei der Betrachtung der frequenzabhängigen Spannungsverstärkung geeigneter, da damit die „zeitliche Verschiebung“ (Phase) von der Verstärkung getrennt werden kann.
Weg zum Bodediagramm
Um die Frequenzabhängigkeit des Betrags der Spannungsverstärkung besser verstehen zu können, kann diese als $|A_V(f)|$ in Abhängigkeit zur Frequenz aufgetragen werden. Dabei bietet es sich an die Spannungsverstärkung als Pegel $|A_V^{dB}(f)|$ darzustellen. In der Simulation rechts ist der Verlauf $|A_V^{dB}(f)|$ für einen Tiefpass in der unteren Bildhälfte zu sehen. Der Verlauf beginnt bei $0dB$ auf der linken Seite und fällt bis etwa $-45dB$ ab. Wenn die Maus über das Diagramm gezogen wird, kann für jeden Frequenz der Verstärkungswert in $dB$ dargestellt werden. Beim Klick auf den Verlauf werden Stromfluss und Spannungsverhältnisse dargestellt. Nur bei Klick auf den äußersten, linken Frequenzbereich ergibt sich eine Situation, in der $U_A$ merklich hohe Spannungen annimmt (sichtbar über die Farbe der Leitung).
In dieser Darstellungsart ist es schwer Werte, wie z.b. die Grenzfrequenz aus dem Frequenzverlauf zu ermitteln.
Wird aber auch die Frequenzachse logarithmiert, ergibt sich ein anderes Bild. Dies erfolgt über Options » Linear Scale. Nun wird der zunächst flache Verlauf der Spannungsverstärkung für geringe Frequenzen und der Abfall für höhere Frequenzen sehr deutlich. Auch die Grenzfrequenz ist im „Knick“ ablesbar.
Die Phase kann über Options » Show Phase sichtbar gemacht werden.
Beschreibung des Bodediagramms
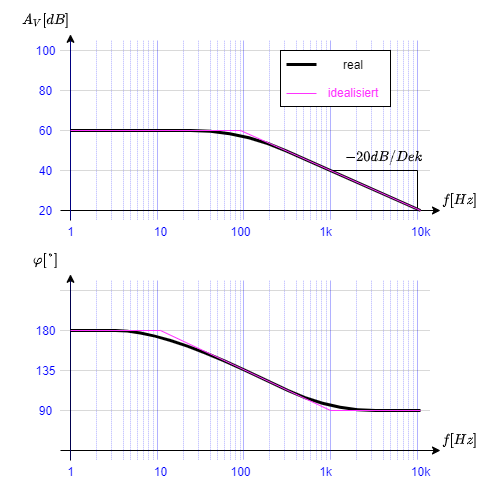
Das Bodediagramm ermöglicht die Darstellung einer komplexwertigen, frequenzabhängigen Größe in logarithmischer Form. Es wird auch als Frequenzgang bezeichnet und unterteilt sich in (vgl. Abbildung 3):
- den Amplitudengang der die Amplitude doppelt-logarithmisch darstellt (dB-Pegel ist eine logarithmische Darstellung) und
- den Phasengang der die Phase einfach-logarithmisch darstellt
Einen Sprung in der Frequenz um den Faktor $\times 10$ nennt man Dekade (abgekürzt Dek.).
Der Amplitudengang von verschiedenen Funktionen soll kurz besprochen werden ($\mathcal{C}$ ist dabei ein beliebiger frequenzunabhängiger Faktor):
- $|A_V(f)| = \mathcal{C} \cdot f$: Wird eine Funktion betrachtet, die linear mit $f$ ansteigt, so ergibt eine Verzehnfachung der Frequenz eine Verzehnfachung der Spannungsverstärkung. Damit ergibt sich ein Anstieg um $+20dB$ pro Dekade.
- $|A_V(f)| = \mathcal{C} / f$: Wird eine Funktion betrachtet, die sich reziprok zu $f$ verhält, so ergibt eine Verzehnfachung der Frequenz ein Absenken der Spannungsverstärkung auf ein Zehntel. Damit ergibt sich ein Abfall um $-20dB$ pro Dekade (vgl. Abbildung 3 bei hohen Frequenzen).
- $|A_V(f)| = \mathcal{C} / f^n$: Wird eine Funktion betrachtet, die sich reziprok zu $f^n$ verhält, so ergibt eine Verzehnfachung der Frequenz ein Absenken der Spannungsverstärkung auf ein $1/10^n$tel. Damit ergibt sich ein Abfall um $-20dB \cdot n$ pro Dekade.
Alternativ zum tatsächlichen Verlauf werden gelegentlich $|A_V(f)|$ und $\varphi(f)$ auch idealisiert mit Geradenstücken dargestellt.
Merke: Bodediagramm
Für Strom und Spannungspegel gilt:
- Ein linearer Faktor von $\color{green}{\times 10}$ ergibt im Pegel $+ 20dB$
- Ein linearer Faktor von $\color{green}{\times 2}$ ergibt im Pegel $+ 6dB$
- Der linearer Wert $A_V = 1$ entspricht $0 dB$
Bei hintereinander geschalteten Systemen ist für die Ermittlung der Verstärkung
- das lineare Maß $A_V$ zu multiplizieren und
- der Pegel $A_V^{dB}$ zu addieren.
5.1 Umkehrintegrator
Bisher wurden Operationsverstärker-Schaltungen betrachtet, in denen eine Gegenkopplung über ohmsche Widerstände geschah. Im folgenden sollen nun Operationsverstärker-Schaltungen mit speichernden Komponenten ($C$, $L$) analysiert werden.
In der Elektronik wird dabei nur selten auf Induktivitäten zurückgegriffen. Dies hat verschiedene Ursachen:
- Induktivitäten sind zwar in integrierte Schaltkreisen möglich, aber etwas schwerer als solches Element zu berechnen.
- Induktivitäten benötigen als Stromspeicher eine Stromquelle. Durch den internen Widerstand ergibt sich ein kontinuierlicher Leistungsverlust.
Statt Induktivitäten werden in der Mikroelektronik und der Filtertechnik für Sensorsignale Kondensatoren genutzt. Die gebildeten passiven Schaltungen werden entsprechen auch $R$-$C$-Glieder genannt und wurden in Elektrotechnik 2 analysiert.
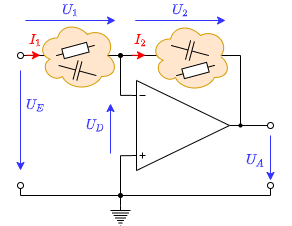
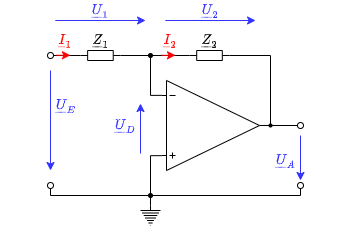
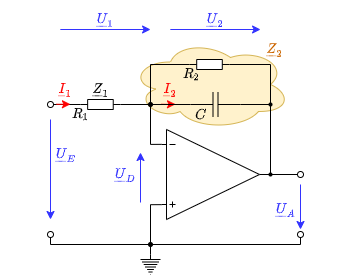
Als Grundschaltung wird im folgenden ein abgewandelter, invertierter Verstärker genutzt (Abbildung 4) in dem einer oder beide ohmsche Widerstände durch (komplexwertige) Impedanzen ersetzt.
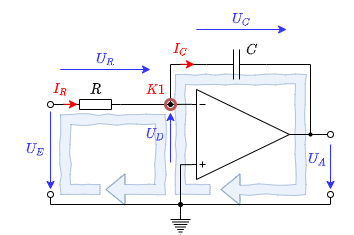
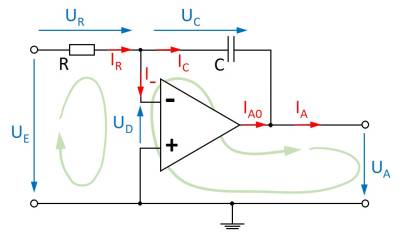
Für erste Schaltung soll nur der Teil zwischen Ausgangsspannung $U_A$ und virtueller Masse durch einen Kondensator ersetzt werden (Abbildung 5).
5.1.1 Schaltungsanalyse mit Differentialgleichungen
Die erste aktive Filterschaltung ist rechts in der Simulation zu sehen. Durch die überlagerten Rechteckspannungsquellen ergibt sich als Eingangsspannung eine Stufenfunktion. Diese erzeugt über das RC-Glied einen Strom. Betrachtet man nun die Ausgangsspannung im Vergleich zur Eingangsspannung, so kann festgestellt werden, dass:
- bei jedem konstanten Eingangswert $U_E \neq 0$ sich ein Ausgangswert mit fester Steigung ergibt und
- bei jedem positiven Eingangswert $U_E > 0$ sich eine negative Steigung, bei negativem Eingangswert eine positive Steigung ergibt.
Die so erstellte Schaltung wird Umkehrintegrator genannt.
Betrachtet man die Schaltung so ist ersichtlich, dass der Knoten $K_1$ auf virtueller Masse liegt. Bei einer konstanten Eingangsspannung ist der Eingangsstrom ist also konstant und nur durch den Widerstand definiert. Damit lädt sich der Kondensator mit einem konstanten Strom auf; die Ladung steigt linear. Die Spannung über den Kondensator steigt somit auch linear.
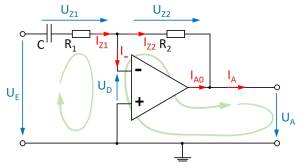
Genauso wie in bei den Grundschaltungen soll nun der Zusammenhang zwischen Ausgangswert und Eingangswert mathematisch ermittelt werden. In Abbildung 5 sind dazu die Maschen eingezeichnet. Es soll nun hier die Übertragungsfunktion $U_A = f(U_E)$ ermittelt werden.
$A_V = ? \quad -> \quad U_A = f(U_E) $
gegebene Gleichungen
Gegeben sind folgende Gleichungen:
| I. | Grundgleichung | $U_A = A_D \cdot U_D$ |
| II. | Masche 1 | $ -U_E+U_R-U_D=0 $ |
| III. | Masche 2 | $U_D+U_C+U_A=0$ |
| IV. | Knoten | $I_R=I_C$ |
| V. | Kapazität C | $C= { Q \over U_C } = { 1 \over U_C }\cdot(\int_{t_0}^{t_1} I_C dt+ Q_0(t_0)) $ |
| VI. | Widerstand R | $R = { U_R \over I_R }$ |
Herleitung
| $U_A = f(U_E)$ | mit III. | |
| $U_A=\color{blue}{-U_D}-U_C$ | mit II. und I. | $ \color{blue}{U_D} = { 1 \over A_D } \cdot U_A \overset{A_D -> \infty}\longrightarrow 0$ |
| $U_A= \quad \quad 0 \quad -\color{blue}{U_C}$ | mit V. | $\color{blue}{U_C}={ 1 \over C }\cdot(\int_{t_0}^{t_1} I_C \ dt+ Q_0(t_0))$ |
| $U_A = -{ 1 \over C }\cdot(\int_{t_0}^{t_1} \color{blue}{I_C} \ dt+ Q_0(t_0)) $ | mit IV. | $\color{blue}{I_C}=I_R$ |
| $U_A = \color{blue}{-{ 1 \over C }\cdot(}\int_{t_0}^{t_1} I_R \ dt+ Q_0(t_0)\color{blue}{)} $ | Ausklammern | |
| $U_A = -{ 1 \over C }\cdot\int_{t_0}^{t_1} I_R \ dt - \color{blue}{ Q_0(t_0) \over C } $ | Integrationskonstante betrachten | $\color{blue}{ Q_0(t_0) \over C }= U_C(t_0) = -U_{A0}$ |
| $U_A = -{ 1 \over C }\cdot\int_{t_0}^{t_1} \color{blue}{I_R} \ dt + U_{A0}$ | mit VI. und II. | $\color{blue}{I_R}={ U_R \over R}={ U_E \over R} $ |
| $U_A = -{ 1 \over C }\cdot\int_{t_0}^{t_1} \color{blue}{1 \over R} \cdot U_E \ dt + U_{A0}$ | Konstante vorziehen | |
| $U_A = -{ 1 \over {R\cdot C} }\cdot\int_{t_0}^{t_1} U_E \ dt + U_{A0}$ | Zeitkonstante $\tau = R \cdot C$ einfügen | |
$U_A = -{ 1 \over {\tau} }\cdot\int_{t_0}^{t_1} U_E \ dt + U_{A0}$ |
5.1.2 Signal-Zeit-Verlauf
Anhand eines Beispiels soll der Signal-Zeit-Verlauf am Umkehrintegrator erklärt werden.
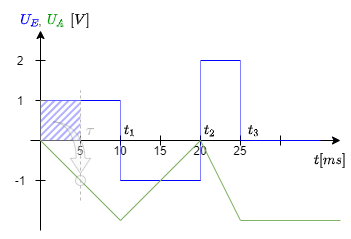
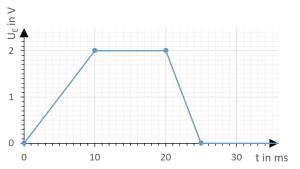
- Gegeben sei $R=5 k\Omega$, $C=1 \mu F$ und der in Abbildung 6 abgebildete Verlauf der Eingangsspannung $U_E$
- Gesucht ist die Ausgangsspannung $U_A$
Lösung:
- Über die gegebenen Werten von $R$ und $C$ wird die Zeitkonstante $\tau$ bestimmt
- Beim Umkehrintegrator wird der Eingangswert integriert und invertiert. Für den gegebenen Verlauf der Eingangsspannung ist also die Berechnung von Stützstellen ausreichend
- Mit der in 5.1.1 hergeleiteten Formel lässt sich $U_A$ abschnittsweise zusammensetzen:
- Am Punkt $t_1$:
$U_{A}(t_1) \ \ = \ -{ 1 \over {\tau} } \ \cdot \ \int_{t_0}^{t_1} U_E \ dt \ + \ U_{A}(t_0) = -{ 1 \over {5 k\Omega \cdot 1 \mu F} }\cdot\int_{0}^{10ms} 1V \ dt + 0V$
$\qquad \qquad = -{ 1 \over {5 ms} } \quad \cdot 1V \ \cdot \int_{0}^{10ms} \ dt \qquad \ = \ -{ 1 \over {5 ms} }\ 1V \ [t]_{0}^{10ms} = -2V$
- Am Punkt $t_2$:
$U_{A}(t_2) \ \ = \ -{ 1 \over {\tau} } \ \cdot \ \int_{t_1}^{t_2} U_E \ dt \ + \ U_{A}(t_1) = -{ 1 \over {5 ms} }\cdot (-1V) \cdot [t]_{10ms}^{20ms} + 2V = 0V \quad$
- Am Punkt $t_3$:
$U_{A}(t_3) \ \ = \ -{ 1 \over {\tau} }\ \cdot \ \int_{t_2}^{t_3} U_E \ dt \ + \ U_{A}(t_2) = -{ 1 \over {5 ms} }\cdot (-2V) \cdot [t]_{20ms}^{25ms} + 0V = -2V \quad$
Merke: Signal-Zeit-Verlauf des Umkehrintegrators
Wird am Umkehrintegrator eine konstante Eingangsspannung $U_E$ angelegt, so entspricht die Ausgangsspannung $U_A$ nach der Zeitkonstante $\tau$ gerade $-U_E$ (siehe Abbildung 6, hellgrauer Pfeil).
5.1.3 Ermittlung von Betrag und Phase
Um Betrag und Phase ermitteln zu können, sollen zunächst rein sinusförmige Eingangs- und Ausgangsgrößen betrachtet werden.
Als Eingangsspannung $U_E$ wird folgende Funktion genutzt:
$ U_E(t)= \hat{U}_E \cdot sin(\omega \cdot t)$
Diese Definition der Eingangsspannung kann nun in die obige Gleichung für $U_A$ eingesetzt werden:
| $U_A = -{ 1 \over {R\cdot C} }\cdot\int_{t_0}^{t_1} \color{blue}{U_E(t)} \ dt + U_{A0}$ | Sinusfunktion einsetzen | $ \color{blue}{U_E(t)}= \hat{U}_E \cdot sin(\omega \cdot t)$ |
| $U_A = -{ 1 \over {R\cdot C} }\cdot\color{blue}{\int_{t_0}^{t_1} \hat{U}_E \cdot sin(\omega \cdot t) \ dt} + U_{A0}$ | Stammfunktion mit Grenzen einsetzen | $\color{blue}{\int_{x_0}^{x_1} sin(a \cdot x) \ dx} = [- {1 \over a} \cdot cos(a \cdot x) ]_{x_0}^{x_1}$ |
| $U_A = -{ 1 \over {R\cdot C} }\cdot [- \color{blue}{\hat{U}_E \over \omega} \cdot cos(\omega \cdot t) ]_{t_0}^{t_1} + U_{A0}$ | Konstante vor Integral setzen | |
| $U_A = { 1 \over {R\cdot C} }\cdot {\hat{U}_E \over \omega} \cdot \color{blue}{[ cos(\omega \cdot t) ]_{t_0}^{t_1}} + U_{A0}$ | Grenzwerte einsetzen | $t_0=0$, $t_1=t$ |
| $U_A = { {\hat{U}_E } \over {\omega \cdot R\cdot C} } \cdot ( cos(\omega \cdot t) - \color{blue}{cos(0)} ) + U_{A0}$ | $\color{blue}{cos(0)}=1$ | |
| $U_A = \color{blue}{{{ \hat{U}_E } \over {\omega \cdot R\cdot C} } \cdot (} cos(\omega \cdot t) - 1 \color{blue}{)} + U_{A0}$ | Ausmultiplizieren | |
| $U_A = { {\hat{U}_E } \over {\omega \cdot R\cdot C} } \cdot cos(\omega \cdot t) \color{blue}{-{ {\hat{U}_E } \over {\omega \cdot R\cdot C}} + U_{A0}}$ | Betrachtung der nicht-Kosinus-Terme | Dieser Teil ist zeitlich unabhängig. Da wir von rein sinusförmigen Größen ausgehen, muss die für die anfängliche Spannung des Kondensators gelten: $U_{C0} = U_{A0}={{\hat{U}_E} \over {\omega \cdot R\cdot C}}$ |
$U_A = { {\hat{U}_E } \over {\omega \cdot R\cdot C} } \cdot cos(\omega \cdot t)$ |
Der Betrag $|A_v|$ ist über das Amplitudenverhältnis von $\hat{U}_A \over \hat{U}_E$ gegeben: $$|A_v|={\hat{U}_A \over \hat{U}_E} = {1 \over {\omega \cdot R\cdot C}} $$
Die Phase lässt sich aus dem „zeitlichen Versatz“ des Spitzenwerts von Eingangsspannung $U_E = \hat{U}_E \cdot sin(\omega \cdot t)$ und Ausgangsspannung $U_A = { {\hat{U}_E } \over {\omega \cdot R\cdot C} } \cdot cos(\omega \cdot t)$ ermitteln. Die Phase ist durch die Betrachtung der trigonometrischen Funktionen und dem Vorzeichen gegeben:
$U_E = + \hat{U}_E \cdot sin(\omega \cdot t)$
$U_A = + \hat{U}_A \cdot cos(\omega \cdot t) = + \hat{U}_A \cdot sin(\omega \cdot t + 90°)$
$ \rightarrow \ \varphi = 90°$
Extremalwertbetrachtung
Um den den Verlauf im Bodediagramm skizzieren zu können, soll das Verhalten der Übertragungsfunktion $U_A=f(U_E)$ in den Extremfällen für niedrige (${\omega}\rightarrow 0$) und hohe Frequenzen (${\omega}\rightarrow \infty$) betrachtet werden. Für Betrag $|A_v|$ und Phase $\varphi$ ergibt sich:
$ |A_v({\omega}\rightarrow 0 \ \; )| \quad=\quad{1 \over {\color{blue}{\omega} \cdot R\cdot C}} \quad\xrightarrow{\color{blue}{\omega}\rightarrow 0}\quad \infty$
$ |A_v({\omega}\rightarrow\infty)| \quad=\quad{1 \over {\color{blue}{\omega} \cdot R\cdot C}} \quad\xrightarrow{\color{blue}{\omega}\rightarrow\infty}\quad 0$
$\varphi = +90° \qquad \forall \ \omega$
Aus diesen Randbedingungen lässt sich bereits der Frequenzgang skizzieren, siehe Abbildung 7.
5.1.4 Schaltungsanalyse mit komplexer Rechnung
In den vorherigen Kapiteln war zu sehen, dass die Schaltungsanalyse mit Differentialgleichungen bereits bei einer einfachen Schaltung wie dem Umkehrintegrator sehr zäh und rechenintensiv ist. Es soll nun die komplexe Rechnung als eine Methode betrachtet werden, welche die Analyse solcher Schaltungen vereinfacht. Für die komplexe Rechnung werden die Widerstände und Kapazitäten durch komplexe Impedanzen ersetzt:
$U_R=R\cdot I \qquad \qquad \qquad \qquad \qquad \rightarrow \underline{U}_} = R \cdot \underline{I}$
$U_C={ 1 \over C }\cdot(\int_{t_0}^{t_1} I_C \ dt+ Q_0(t_0)) \qquad \rightarrow \underline{U}_C = \underline{Z}_C \cdot \underline{I} \quad$ mit $\quad \underline{Z}_C= \frac{1}{j \cdot \omega \cdot C}$
Diese Betrachtung kann aber nur unter bestimmten Randbedingungen umgesetzt werden:
- sinusförmige Größen: komplexe Strom- bzw. Spannungszeiger (vgl. ET2 Wechselstromtechnik) können nur sinusförmige Größen abbilden.
- eingeschwungener Zustand: Die Gleichungssysteme betrachten nur sinusförmige Schwingungen, die seit unendlicher Zeit bereits bestehen. Dies entspricht einer langen Zeit seit dem Einschalten. Damit werden Störungen, die durch das Einschalten erzeugt werden, herausgenommen.
Damit kann nun die Schaltung (Abbildung 8) berechnet werden:
$\underline{Z}_1=R$
$\underline{Z}_2=\frac{1}{j \cdot \omega \cdot C} = \frac{-j}{\omega \cdot C}$
Von der Grundschaltung des invertierenden Verstärkers ist dessen Spannungsverstärkung bekannt:
$A_V = \frac{U_A}{U_E}=-\frac{R_2}{R_1}$
Dies ergibt im Komplexen:
$\underline{A}_V = \frac{\underline{U}_A}{\underline{U}_E}=-\frac{\underline{Z}_2}{\underline{Z}_1} = \frac{j}{\omega \cdot R \cdot C} $
Plausibilisierung über Extremalwertbetrachtung
| Aus der Formel | Aus der Schaltung |
|---|---|
| $\underline{A}_V \xrightarrow{\omega \rightarrow 0} \infty$ | Für $\omega \rightarrow 0$ wird aus dem Kondensator eine hochohmiger Widerstand Der Operationsverstärker muss für $\underline{U}_D \rightarrow 0$ eine Ausgangspannung von $\underline{U}_A \rightarrow \infty$ ausgeben. |
| $\underline{A}_V \xrightarrow{\omega \rightarrow \infty} 0$ | Für $\omega \rightarrow \infty$ wird aus dem Kondensator ein Kurzschluss Der Operationsverstärker muss für $\underline{U}_D \rightarrow 0$ eine Ausgangspannung von $\underline{U}_A \rightarrow 0$ ausgeben. |
Betrag und Phase
Als Betrag $A_V$ ergibt sich:
$|\underline{A}_V|= \frac{1}{\omega \cdot R \cdot C} \sim \frac{1}{f}$
Speziell wird ergibt sich für einen Betrag von $|\underline{A}_V(0dB)|$ bei $0dB$:
$|\underline{A}_V(0dB)|\overset{!}{=} 1 \widehat{=} 0dB \rightarrow \omega(0dB) = \frac{1}{R \cdot C}$
Die Phase $\varphi$ berechnet sich über
$\varphi = arctan \left( \frac{\Im(\underline{A}_V)}{\Re(\underline{A}_V)} \right) = arctan \left( \frac{\omega \cdot R \cdot C}{0} \right) = arctan \left( \infty \right) = +90°$
Die Phase $\varphi=+90°$ für $arctan(x)|_{x\rightarrow \infty}$ ist auch aus dem Verlauf des Arkustangens (Abbildung 9) für $x \rightarrow \infty$ ersichtlich.
5.1.5 Frequenzgang
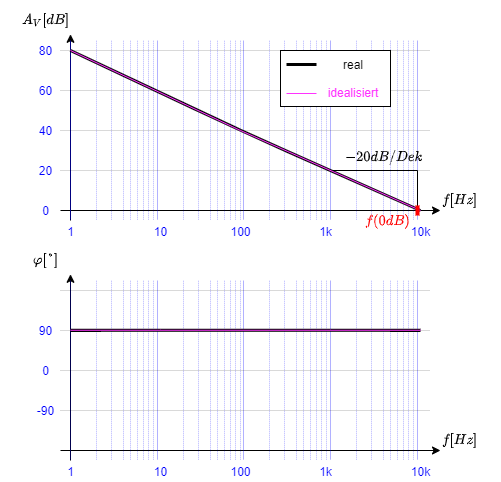
Der Frequenzgang soll anhand eines Beispiels dargestellt werden.
- Gegeben sei $R=1 k\Omega$, $C=16 nF$
- Gesucht ist das Bode-Diagramm
Lösung
- Bestimmung der Zeitkonstante:
$\tau = R \cdot C = 16 \mu s$
- Ermittlung der Frequenz $f$ für $|\underline{A}_V(0dB)|$: $\omega(0dB)= \frac{1}{\tau} = 2\pi \cdot f(0dB)$
Damit ergibt sich $f(0dB)$ über:
$f(0dB)=\frac{1}{2\pi} \cdot \frac{1}{16 \mu s} \approx 10kHz$
- Betrachtung der Steigung:
$|\underline{A}_V|= \frac{1}{\omega \cdot R \cdot C} \sim \frac{1}{f}$
Daraus ergibt sich für eine Verzehnfachung von $f$ ein Zehntel des Betrags $|\underline{A}_V|$, also eine Steigung um $-20dB$ pro Dekade
- Aus diesen Informationen lässt sich das vollständige Bode-Diagramm ermitteln (Abbildung 10)
5.2 Tiefpass
In der Simulation können durch die Schalter verschiedene Rückkoppelpfade deaktiviert werden. Damit wird die Schaltung zum Umkehrintegrator oder zum invertierenden Verstärker. Unten in der Simulation ist das Bode-Diagramm skizziert. Mit Klick auf das Bode-Diagramm wird die zur Frequenz passende Aufteilung des Stroms in der Schaltung dargestellt.
Die Schaltung soll im Folgenden aus zwei Richtungen betrachtet werden: Einerseits kann bereits ohne ausführliche Rechnung ein gutes Bild des Systemwirkung erstellt werden. Diese soll im Anschluss durch eine Schaltungsanalyse mit komplexer Rechnung überprüft werden.
5.2.1 Betrachtung ohne ausführliche Rechnung
Extremalwertbetrachtung
Aus der Betrachtung des Kondensators für $\omega \rightarrow 0$ und $\omega \rightarrow \infty$ kann der Verlauf von Betrag der Spannungsverstärkung und Phase analysiert werden.
- $\omega \rightarrow 0$:
- Der Kondensator wirkt wie eine offene Leitung
- Damit ist die Impedanz des Kondensators größer als die des Widerstands: $R_2 \ll |\underline{X}_C|$
- Damit wirkt in der Parallelschaltung von $R_2$ und $C$ im wesentlichen $R_2$
- Damit verhält sich die Schaltung wie ein invertierender Verstärker: $|\underline{A}_V|=|-\frac{R_2}{R_1}|$
- Für den invertierender Verstärker ergibt sich für ein sinusförmiges Eingangssignal eine negiertes, sinusförmiges Signal. Die entspricht einer Phase von $\varphi=\pm 180°$. Das Vorzeichen ist dabei nicht durch den invertierender Verstärker definiert.
- $\omega \rightarrow \infty$:
- Der Kondensator wirkt wie ein Kurzschluss
- Damit ist die Impedanz des Kondensators kleiner als die des Widerstands: $R_2 \gg |\underline{X}_C|$
- Damit wirkt in der Parallelschaltung von $R_2$ und $C$ im wesentlichen $C$
- Damit verhält sich die Schaltung wie ein Umkehrintegrator: $|\underline{A}_V|=|-\frac{1}{\omega \cdot R_1 \cdot C}|$ und $\varphi=+ 90°$
Daraus wird ersichtlich, dass
- für geringe Frequenzen eine konstante Verstärkung erwartet wird und
- für hohe Frequenzen ein Abfall wie er vom Umkehrintegrator bekannt ist.
erwartetes Bodediagramm
Aus der Extremalwertbetrachtung lässt sich ein Bodediagramm abschätzen.
Frequenzgang:
- Für geringe Frequenzen verhält sich das Filter wie ein invertierender Verstärker mit $|\underline{A}_V|=|-\frac{R_2}{R_1}|$
- Für höhere Frequenzen verhält sich das Filter wie ein Umkehrintegrator mit $|\underline{A}_V|=|-\frac{1}{\omega \cdot R_1 \cdot C}|$
- Es gibt eine Frequenz, in der beide Situationen gleichzeitig aufzutreten scheinen
Phasengang:
- Für geringe Frequenzen verhält sich das Filter wie ein invertierender Verstärker mit $\varphi=\pm 180°$
- Für höhere Frequenzen verhält sich das Filter wie ein Umkehrintegrator mit $\varphi=+90°$
- Es gibt eine Frequenz, in der beide Situationen gleichzeitig aufzutreten scheinen
Für den Zwischenbereich muss es einen Übergang zwischen den beiden extremalen Situationen geben.
Ein Problem scheint noch zu sein, dass für den invertierenden Verstärker nicht klar ist, ob die Phase nun $+180°$ oder $-180°$ ist. In der mathematischen Betrachtung des Umkehrintegrator hat sich herausgestellt, dass für einen Kondensator ein Integrationsschritt ($U=\frac{1}{C} \int I_C \ dt$) durchgeführt werden muss. Im invertierenden Verstärker war kein Integrationsschritt notwendig. Damit wird ein sinusförmiges Eingangssignal maximal um 90° verschoben. Es muss also von invertierenden Verstärker bei niedrigen Frequenzen gerade $90°$ Phasenverschiebung zu hohen Frequenzen geben.
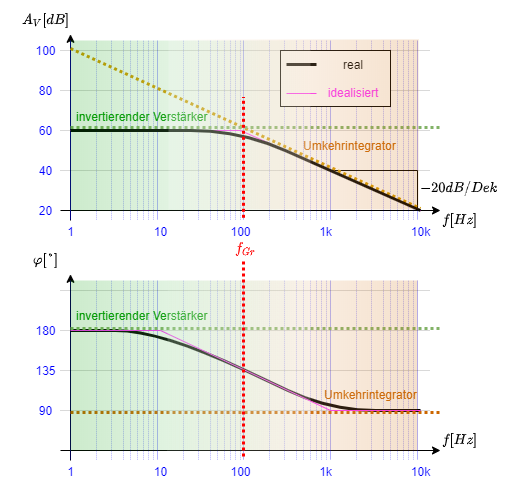
Aus diesen Kenntnissen ergibt sich ein erwartetes Bodediagramm wie in Abbildung 12 zu sehen.
Merke: Filter im Bodediagramm
Folgende Regeln gelten für Filter:
- je vorhandenem Energiespeicher erhöht sich die Ordnung des Filters um 1
- je vorhandenem Energiespeicher ($C$, $L$) ergibt sich eine Amplitudenänderung von $-20dB/Dek$
- je vorhandenem Energiespeicher ($C$, $L$) ergibt sich eine Phasenänderung von $-90°$
- Der Phasengang ist monoton fallend.
RC-Glied und Grenzfrequenz
In der Schaltung verhält sich die Parallelschaltung $R_2$ und $C$ wie ein passives RC-Glied. Das bedeutet, es wirkt sich auf das Frequenzverhalten aus. Bei einer bestimmten Frequenz verhält sich die Schaltung gerade so, dass der Strom hälftig über $R_2$ und $C$ läuft, also „halb“ wie ein invertierender Verstärker und „halb“ wie ein Umkehrintegrator wirkt. Diese Frequenz ist die Grenzfrequenz $f_{Gr}$:
Dafür gilt:
$|\underline{X}_C|=R_2$
$\frac{1}{\omega_{Gr} \cdot C}=R_2 \rightarrow \omega_{Gr} = \frac{1}{R_2 \cdot C} = 2\pi \cdot f_{Gr}$
$\boxed{f_{Gr} = \frac{1}{2\pi \cdot R_2 \cdot C}} $
5.2.2 Schaltungsanalyse mit komplexer Rechnung
Es soll nun die Schaltung wieder mittels komplexer Rechnung analysiert werden. Dabei der werden die Impedanzen wieder als komplexe Zahl aufgefasst. Den Ausgangspunkt bildet wieder die Spannungsverstärkung des (komplexen) invertierenden Verstärker. Dabei werden die Impedanzen aus Abbildung 11 berücksichtigt:
$\underline{A}_V=\frac{-\underline{Z}_2}{\underline{Z}_1}=\frac{-R_2||C}{R_1}=\frac{-\frac{R_2 \cdot \frac{1}{j \cdot \omega \cdot C}}{R_2 + \frac{1}{j \cdot \omega \cdot C}}}{R_1}=\frac{-R_2}{R_1 \cdot R_2 \cdot \omega \cdot C + R_1}$
$\boxed{\underline{A}_V= - \frac{R_2}{R_1}\cdot \frac{1}{1 + j \omega \cdot R_2 \cdot C}}$
Berechnung von Betrag und Phase
Für die Berechnung des Betrags $A_V$ kann ein „Trick“ angewandt werden. Prinzipiell kann der Betrag immer durch die Multiplikation mit dem konjungiert komplexen Wert ermittelt werden. Hier ist es aber einfacher den Betrag des Bruchs über den Betrag von Zähler und Betrag von Nenner zu berechnen:
$|\underline{A}_V| = |... \cdot \frac{...}{...}| = |...| \cdot \frac{|...|}{|...|}$
Damit ergibt sich für den Betrag:
$\boxed{|\underline{A}_V| = \frac{R_2}{R_1}\cdot \frac{1}{\sqrt{1^2 + (\omega \cdot R_2 \cdot C)^2}}}$
Für die Phase $\varphi$ muss nun doch Realwert $\Re(\underline{A}_V)$ und Imaginärwert $\Im(\underline{A}_V)$ über die Multiplikation mit dem konjungiert komplexen Wert ermittelt werden.
$\varphi = arctan(\frac{\Im(\underline{A}_V)}{\Re(\underline{A}_V)})$
Aber auch hier gibt es einen „Trick“:
$\underline{A}_V= \color{blue}{- \frac{R_2}{R_1}\cdot \frac{1}{1 + j \omega \cdot R_2 \cdot C}} \cdot \frac{1 - j \omega \cdot R_2 \cdot C}{\color{blue}{1 - j \omega \cdot R_2 \cdot C}}$
Es wird ja gerade der konjungiert komplexe Wert multipliziert, um einen reellen Nenner zu erhalten. Damit ist der blau markierte Teil eine reale Konstante $\mathcal{C}$:
$\underline{A}_V= \color{blue}{\mathcal{C}} \cdot (1 - j \omega \cdot R_2 \cdot C)$
Damit ergibt sich die Phase $\varphi = arctan\left(\frac{\color{teal}{\Im(\underline{A}_V)}}{\color{brown}{\Re(\underline{A}_V)}}\right)$ als
$\underline{A}_V= \mathcal{C} \cdot (\color{brown}{1} + j \cdot \color{teal}{-\omega \cdot R_2 \cdot C})$
$\boxed{\varphi = arctan\left(\frac{\color{teal}{-\omega \cdot R_2 \cdot C}}{\color{brown}{1}}\right)}$
Extermalwertbetrachtung
Für den Betrag ergibt sich
- bei $\omega \rightarrow 0$:
$|\underline{A}_V| = \frac{R_2}{R_1}\cdot \frac{1}{\sqrt{1^2 + \color{blue}{(\omega \cdot R_2 \cdot C)^2}}} \rightarrow \frac{R_2}{R_1}\cdot \frac{1}{\sqrt{1^2 }}$, da $\color{blue}{(\omega \cdot R_2 \cdot C)^2} \gg 1$
Der Betrag der Verstärkung geht also gegen $|\underline{A}_V| = \frac{R_2}{R_1}$.
Die Wirkung gleicht dem invertierenden Verstärker
- bei $\omega \rightarrow \infty$:
$|\underline{A}_V| = \frac{R_2}{R_1}\cdot \frac{1}{\sqrt{1^2 + \color{blue}{(\omega \cdot R_2 \cdot C)^2}}} \rightarrow \frac{R_2}{R_1}\cdot \frac{1}{\sqrt{\color{blue}{(\omega \cdot R_2 \cdot C)^2}}} $, da $\color{blue}{(\omega \cdot R_2 \cdot C)^2} \ll 1$
Der Betrag der Verstärkung geht also gegen $|\underline{A}_V| = \frac{1}{\sqrt{\color{blue}{(\omega \cdot} R_1 \color{blue}{\cdot C)^2}}}$.
Die Wirkung gleicht dem Umkehrintegrator
Für die Ermittlung der Phase $\color{red}{\varphi} = arctan\left(\color{teal}{-\omega \cdot R_2 \cdot C}\right)$ hilft es den Arkustangens im Diagramm zu betrachten. Dazu wird das Argument $Arg = \color{teal}{-\omega \cdot R_2 \cdot C}$ gegen die Phase $\color{red}{\varphi}$ aufgetragen (Abbildung 13). Für die Extremalwerte $\omega$ von ergibt sich
- bei $\omega \rightarrow 0$:
Das Argument $Arg = \color{teal}{-\omega \cdot R_2 \cdot C}$ geht gegen $-0$. Der Punkt $Arg \rightarrow -0$ entspricht gerade dem Annähern an die y-Achse (hier $\varphi$-Achse) von links in Abbildung 13. - bei $\omega \rightarrow \infty$:
Das Argument $Arg = \color{teal}{-\omega \cdot R_2 \cdot C}$ geht gegen $-\infty$. Der Punkt $Arg \rightarrow -\infty$ entspricht gerade dem Weg nach links im Diagramm.
Es
Berechnung der Grenzfrequenz
Bei der Grenzfrequenz lässt sich auch so verstehen, dass dort gerade der Übergang vom invertierenden Inverter zum Umkehrintegrator stattfindet. Im Bode-Diagramm (Abbildung 12) ist die Grenzfrequenz gerade beim Schnittpunkt der Geraden für invertierenden Inverter und Umkehrintegrator zu finden.
Es ergibt sich also für die Grenzfrequenz $f_{Gr}$
$\frac{R_2}{R_1} = \frac{1}{\omega_{Gr} R_1 \cdot C}$
$\omega_{Gr} = \frac{1}{ R_2 \cdot C} = 2 \pi \cdot f_{Gr}$
Aufgaben
Aufgabe 5.0.1. Umwandlung linearer Faktoren in dB
Leiten Sie für folgende Pegel in dB den linearen Faktor her. Geben Sie an, wie dieser Faktor jeweils über die Stützstellen 20 dB ≙ Faktor 10 und 6 dB ≙ Faktor 2 ermittelt werden kann.
Lösen Sie die Aufgabe ohne Taschenrechner
(Hinweis: $\sqrt{2}\approx 1,414$, ${1\over\sqrt{2}}\approx 0,707$)
Als Beispiel ist für den Wert $10 dB$ die Herleitung skizziert.
| Pegel | über Stützstellen in dB | über Stützstellen linear | linearer Faktor |
|---|---|---|---|
| $10 dB$ | $5 \cdot 6 dB - 20 dB$ | $2^5 \cdot {1\over 10}$ | $3,2$ |
| $2 dB$ | |||
| $4 dB$ | |||
| $6 dB$ | |||
| $8 dB$ | |||
| $12 dB$ | |||
| $14 dB$ | |||
| $16 dB$ | |||
| $18 dB$ | |||
| $15 dB$ | |||
| $79 dB$ | |||
| $128 dB$ |
Aufgabe 5.0.2. Analyse von Schaltungen in Tina TI
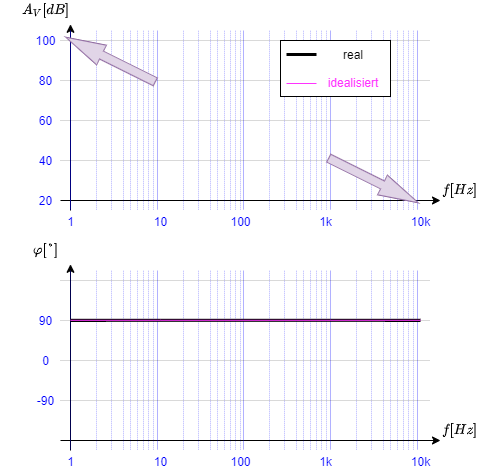
Gegeben sei nebenstehende Schaltung mit $R= 10 k\Omega$, $C = 1,6 uF$ und einer sinusförmigen Eingangsspannung $U_E = 1 V $ mit $f = 1 kHz$. Wie im Kurs beschrieben, lässt sich das Bode-Diagramm in Tina TI über Analysis > AC Analysis > AC Transfer Characteristic darstellen. Relevant sind im folgenden Frequenzen von 100 Hz bis 1 GHz.
- Simulieren Sie diese Schaltung in Tina TI
- mit einem idealen Operationsverstärker
- mit den Operationsverstärkern uA776, LM301A und LM318.- Fügen Sie das Bode-Diagramm an.
- Beschreiben Sie kurz die Unterschiede im Amplitudenverlauf der Verstärkung $A_V$.
- Was passiert, wenn statt $R= 10 k\Omega$, $C = 1,6 uF$ die gleiche Zeitkonstante mit $R= 10 M\Omega$, $C = 1,6 nF$ umgesetzt wird? Überprüfen Sie dies anhand des Vergleichs des Bode-Diagramms des Operationsverstärkers LM318.
- Simulieren Sie einen invertierenden Verstärker in Tina TI. Ersetzen Sie dazu in der Schaltung den Kondensator durch einen Widerstand $R_2 = 10 k\Omega$ und verwenden Sie den Operationsverstärker LM318.
- Fügen Sie das Bode-Diagramm an.
- Wie sollte das Bode-Diagramm (Amplituden- und Phasengang) für einen idealen invertierenden Verstärker aussehen? Welche Abweichung stellen Sie beim realen Aufbau fest?
- Bis zu welcher Frequenz lässt sich die Schaltung als invertierenden Verstärker betreiben (maximale Abweichung von 1dB)? Verwenden Sie Zoom und/oder Cursor zur Ermittlung.
- Simulieren Sie einen open-loop Operationsverstärker LM318 (d.h. ohne Rückkopplungs-Netzwerk). Der nicht-invertierende Eingang soll dabei an Masse liegen. Am invertierenden Eingang soll die oben genannte sinusförmige Eingangsspannung anliegen.
- Fügen Sie das Bode-Diagramm an.
- Welche Grenzfrequenz ergibt sich?
- Mit wieviel dB pro Dekade fällt der Amplitudengang bei hohen Frequenzen ab?
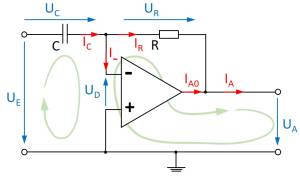
Aufgabe 5.2.1. Umkehrdifferentiator
Leiten Sie für den rechts dargestellten Umkehrdifferentiator die komplexe Spannungsverstärkung, sowie deren Betrag und Phase mittels komplexer Rechnung wie oben dargestellt her. Zeichnen Sie zusätzlich ein passendes Bode-Diagramm
- Schaltungsanalyse mittels Differentialgleichung
- Ermittlung von Betrag und Phase aus Differentialgleichung (incl. Betrachtung der Extremfälle)
- Beispiel eines Signal-Zeit-Verlaufs mit: $R = 10 k\Omega$ und $C = 2µF$ und $U_E$ wie rechts dargestellt
- Schaltungsanalyse mittels komplexer Rechnung
- Betrachtung von Betrag und Phase für $\omega \rightarrow 0$ und $\omega \rightarrow \infty$
- Frequenzgang (Bode-Diagramm) für Schaltung mit: $R = 10 k\Omega$ und $C = 16nF$
Aufgabe 5.2.1 Tiefpass 1. Ordnung
Bevor der Tiefpass in der Vorlesung durchgesprochen wird, sollen hier bereits die Grundlagen dazu gelegt werden. versuchen Sie folgende Fragen zu beantworten:
- Welchen Amplitudengang erwarten Sie für einen Tiefpass?
- Untersuchen Sie folgende Simulation in Falstad. In der Schaltung kann mit den Schalter S1 und S2 ein Teil des Rückkoppelpfades deaktiviert werden.
- Wie heißen die Schaltungen, welche sich ergeben, wenn jeweils nur ein Schalter geschlossen ist?
- Zunächst sollen beide Schalter geschlossen sein. Wie ändert sich die Amplitude der ausgegebenen Spannung (grüne Linie im Oszilloskop), wenn Sie über den Schieberegler rechts die Frequenz der Eingangsspannung ändern?
- Nun soll die Situation mit beiden Schaltern geschlossen mit der Situation jeweils nur ein Schalter geschlossen verglichen werden. Stellen Sie dazu zunächst eine höhere Frequenz ein (z.B. 20…30 kHz) und vergleichen Sie S1=S2=geschlossen mit nur einem Schalter geschlossen.
Aufgabe 5.2.2 Hochpass 1. Ordnung
In der Vorlesung haben wir die Verstärkung $A_V$ des Tiefpasses 1. Ordnung auf Basis seiner Schaltung hergeleitet. In gleicher Weise soll nun die Verstärkung für einen Hochpass hergeleitet werden.
- Verhalten von Betrag und Phase für $\omega \rightarrow 0$ und $\omega \rightarrow \infty$
- Erwartetes Bode-Diagramm
- RC-Glied und Grenzfrequenz
- Schaltungsanalyse mit komplexer Rechnung
- Berechnung von Betrag und Phase
Lernfragen
- Was beeinflusst die Anstiegszeit einer Verstärkerschaltung?
- Worin unterscheiden sich idealer und realer Operationsverstärker?
Referenzen
- Referenzen zu den genutzten Medien
-
Element Lizenz Link Abbildung 8: Überlagerung von sinusförmigen Schwingungen Public Domain https://en.wikipedia.org/wiki/File:Fourier_transform_time_and_frequency_domains.gif Abbildung 9: Verlauf des Arcustangens CC-BY-SA 4.0 https://de.m.wikipedia.org/wiki/Datei:Arctangent.svg Abbildung 15: Verlauf der Funktion Arcustangens2 CC-BY-SA 3.0 https://de.wikipedia.org/wiki/Datei:Arctangent2.svg