Dies ist eine alte Version des Dokuments!
4. Analyse von Gleichstromnetzen
Die Netzwerkanalyse nimmt in der Elektrotechnik eine zentrale Rolle ein. Sie ist deswegen so wichtig, weil damit die auf den ersten Blick komplizierte Schaltungen und Systeme soweit vereinfacht werden können, um diese zu verstehen und Ergebnisse daraus ableiten zu können.
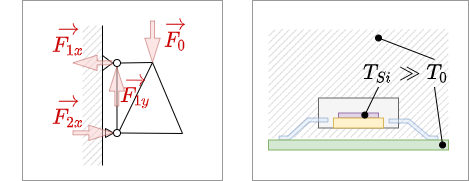
Daneben sind kommen Netzwerke auch in anderen Bereichen vor, zum Beispiel dem Kraftfluss durch ein Fachwerk oder dem Wärmefluss durch einzelne Hardware-Elemente (Abbildung 1). Auch bei diesen Netzwerken können die im Folgenden gezeigten Konzepte angewandt werden.
Ziele
Nach dieser Lektion sollten Sie:
die Anzahl der Knoten, Anzahl der (Baum- und Verbindungs-)Zweige sowie die Anzahl der Maschen ermitteln können.aus einem elektrischen Netzwerk einen vollständigen Baum erstellen können.das Zweigstromverfahren, Maschenstromverfahren und Knotenpotentialverfahren nachvollziehen können.- das Überlagerungsverfahren nachvollziehen und anwenden können.
4.1 Einführung in die notwendigen Begriffe
Erklärung zu Knoten, Zweig, Masche, Graph, vollständiger Baum
4.2 Zweigstromverfahren
Im Zweigstromverfahren werden:
- für alle Knoten k jeweils die Gleichung: $\sum\limits_{i=0}^{N_i}{I_i}=0$ und
- für alle Maschen m jeweils die Gleichung: $\sum\limits_{j=0}^{N_j}{U_j}=0$ aufgeschrieben
Diese können dann als Matrixgleichung betrachtet werden und mit den Regeln der (mathematischen) Kunst gelöst werden.
Im Video 1 werden folgende Schritte beschrieben:
1. Aufschreiben der gegebenen Schaltung und Größen
2. Einzeichnen und Bezeichnen der Knoten
3. Einzeichnen und Bezeichnen der Maschen
Zweigstromanalyse 1/4
Im Video 2 werden folgende Schritte beschrieben:
4. Einzeichnen und Bezeichnen der Zweigströme
5. Einzeichnen und Bezeichnen der Zweigspannungen
Zweigstromanalyse 2/4
Im Video 3 werden folgende Schritte beschrieben:
6. Knotengleichungen und Maschengleichungen aufstellen
7. Umwandeln in Matrix-Schreibweise
Zweigstromanalyse 3/4
Im (hier nicht eingebetteten) Video 4 werden folgende Schritte beschrieben:
8. Einfügen der Zahlenwerte
9. Berechnung der Matrix mittels Taschenrechner
4.3 Maschenstromverfahren
Im Maschenstromverfahren werden nur für alle Maschen m jeweils die Gleichung: $\sum\limits_{j=0}^{N_j}{U_j}=0$ betrachtet. Diese werden aber in der Form $R\cdot I = U $ dargestellt.
Vorteil hierbei: Die Anzahl der zu lösenden Gleichungen reduziert sich auf die Anzahl der unabhängigen Maschenströme.
Auch diese können als Matrixgleichung betrachtet werden und wider mit den Regeln der (mathematischen) Kunst gelöst werden.
Im Video 1 wird anhand eines Beispiels das Maschenstromverfahren angewandt.
Wichtig: Zwar erklärt das Video die Anwendung super, enthält aber bei Minute 6:50 einen kleinen Fehler. Das Vorzeichen der Spannungen auf der rechten Seite muss jeweils invertiert werden. Dies wurde einige Sekunden davor auch richtig erklärt.
Maschenstromanalyse
Auch im Video 2 wird anhand eines Beispiels das Maschenstromverfahren angewandt.
Maschenstromanalyse
Im (hier nicht eingebetteten) Video 3 zeigt ausführlich, wie das Maschenstromverfahren hergeleitet werden kann.
4.4 Knotenpotentialverfahren
Im Knotenpotentialverfahren werden nur für alle Knoten k jeweils die Gleichung: $\sum\limits_{i=0}^{N_i}{I_i}=0$ betrachtet. Diese werden aber in der Form ${1\over R} \cdot U = I $ bzw. $G \cdot U = I $ dargestellt.
Vorteil hierbei: Die Anzahl der zu lösenden Gleichungen reduziert sich auf die Anzahl der vorhandenen Knoten (minus 1).
Auch diese können als Matrixgleichung betrachtet werden und wider mit den Regeln der (mathematischen) Kunst gelöst werden.
Im Video 1 wird die Idee hinter der Knotenpotentialanalyse einfach erklärt.
einfaches Beispiel für eine Knotenpotentialanalyse
Auch im Video 2 wird anhand eines Beispiels das Knotenpotentialverfahren angewandt.
komplexeres Beispiel für eine Knotenpotentialanalyse
Im (hier nicht eingebetteten) Video 3 zeigt ausführlich, wie das Knotenpotentialverfahren hergeleitet werden kann.
4.5 Überlagerungsverfahren / Superpositionsprinzip
Das Superpositionsprinzip soll zunächst durch einige Beispiele dargestellt werden
Beispiel 1 - aus den Vorstellungsgesprächen der Consulting-Branche
Aufgabe: Drei Studierende sollen einen Pool füllen. Wenn Alice diesen alleine füllen würde, so bräuchte sie 2 Tage. Bob bräuchte 3 Tage und Carol bräuchte 4 Tage. Wie lange benötigen alle drei um einen Pool zu füllen, wenn sie zusammenhelfen?
Die Frage klingt zunächst weit weg vom Thema, hat aber unmittelbaren Bezug dazu. Der Punkt ist, dass zur Lösung das Füllen des Pools als linear angenommen wird. Alice wird also $1 \over 2$, Bob $1 \over 3$ und Carol $1 \over 4$ des Pools pro Tag füllen. Am ersten Tag ist also ${1 \over 2}+{1 \over 3}+{1 \over 4} = {{6 + 4 + 3} \over 12} = {13 \over 12}$ des Pools gefüllt. Die drei benötigen also ${12 \over 13}$ eines Tages.
Diese Lösung ist aber nur möglich, da bei linearen Systemen die Teilergebnisse addiert werden können.
Beispiel 2 - Federkraft und -weg
Aufgabe:Eine mechanische, lineare Feder wird mit den Massen $m_1$ und $m_2$ im Gravitationsfeld der Erde ausgelenkt (siehe Abbildung ##). Wie groß ist die Auslenkung, wenn beide Massen gleichzeitig angehängt werden?Auch hier wird ein lineares Gesetz genutzt: \begin{align} \vec{s}= f(\vec{F}) = - D \cdot \vec{F} \end{align}
Es gilt hier der (scheinbar triviale) Ansatz: \begin{align} \vec{s}_{1+2} = f(\vec{F_1} + \vec{F_2}) &= - D \cdot (\vec{F_1} + \vec{F_2}) \\ &= - D \cdot \vec{F_1} - D \cdot \vec{F_2} \\ &= f(\vec{F_1}) + f(\vec{F_2}) \\ &= \vec{s_1} + \vec{s_2} \end{align}
Im Überlagerungsverfahren wird der eine gesuchte Strom (bzw. die eine gesuchte Spannung) in einer Schaltung mit mehreren Quellen als Überlagerung der entstehenden Ströme (bzw. Spannungen) der einzelnen Quellen betrachtet. Das Überlagerungsverfahren (auch Superpositionsprinzip genannt) kann bei verschiedensten physikalischen Aufgabenstellungen genutzt werden. Grundlage dafür ist, dass sich das System linear verhält.
Auf eine Matrix-Darstellung kann hier verzichtet werden.
Im Video 1 wird das Superpositionsprinzips anhand eines einfachen Beispiels erklärt
einfache Betrachtung des Superpositionsprinzips
Auch im Video 2 wird anhand eines Beispiels das Überlagerungsverfahren angewandt.
komplexeres Beispiel für das Überlagerungsverfahren
Tipps
- Auf der Wikiseite zu Netzwerkanalyse sind die verschiedenen Methoden sehr gut kompakt beschrieben
Aufgaben
Aufgabe 4.x.1 Umwandlung eines bipolaren Signals in ein unipolares
Stellen Sie sich vor, Sie wollen entwickeln eine Schaltung entwickeln, welche ein Sensorsignal so konditionieren soll, dass dieses von einem Mikrocontroller verarbeitet werden kann. Das Sensorsignal ist im Bereich $U_{sens} \in [-15...15V]$, der Microcontrollereingang kann Werte einlesen im Bereich $U_{uC} \in [0...3,3V]$. Der Sensor kann einem Strom von maximal $I_{sens,max}=1mA$ liefern. Für den Innenwiderstand des Microcontrollereingangs gilt: $R_{uC} \rightarrow \infty$
Zur Konditionierung soll das Eingangssignal über den Längswiderstand $R_3$ auf das Mittenpotential eines Spannungsteiler $R_1 - R_2$ mit $R_1$ gegen $U_{uC,max}$ geführt werden (ähnliche Schaltung siehe in Simulation rechts).
- Ermitteln Sie den Zusammenhang zwischen $R_1$, $R_2$ und $R_3$ mittels Superposition.
- Ermitteln Sie den Zusammenhang zwischen $R_1$, $R_2$ und $R_3$ mittels Stern-Dreieck Umwandlung.
- Wie groß ist der Eingangswiderstand $R_{in}(R_1, R_2,R_3)$ der Schaltung (betrachtet vom Sensor aus)?
- Wie groß darf der Eingangswiderstand $R_{in}(R_1, R_2,R_3)$ maximal sein, damit der Sensor noch Strom liefern kann?
- Ermitteln Sie geeignete Werte für $R_1$, $R_2$ und $R_3$
- Welche Werte für $R^0_1$, $R^0_2$ und $R^0_3$ aus der E24-Reihe können dazu verwendet werden?
Aufgabe 4.x.2 Übungsaufgabe
Aufgabe 4.x.2 Übungsaufgabe