Aufgabe 2.7.8: Vereinfachen von Schaltungen II (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
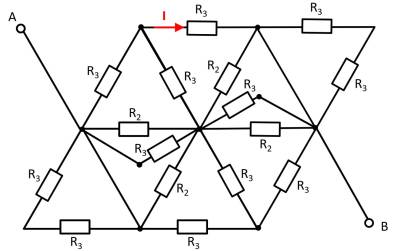
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$R_2=10 \Omega$
$R_3=20 \Omega$
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Schalter (falls vorhanden) sollten dabei durch eine offene oder kurzgeschlossene Leitung ersetzt werden.
- Ergeben sich gleiche Potentiale an verschiedenen Knoten, die geschickt genutzt werden können?
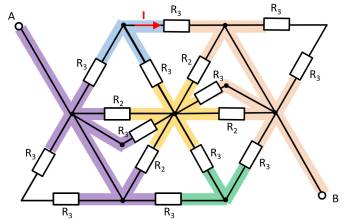
Hierzu können die einzelnen Zweige farbig hervorgehoben und als “leitfähiges Gummiband” interpretiert werden.
Es zeigt sich, dass die beiden Widerstände $R_3$ oben links und unten rechts jeweils kurzgeschlossen sind. Es ergibt sich somit:
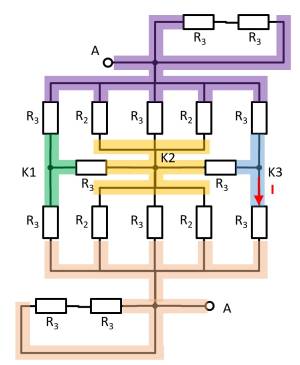
Hier hilft es das Potential der Knoten K1, K2 und K3 zu betrachten. Bei K2 müssen dazu die Widerstände $R_2 || R_3 || R_2$ oben und unten jeweils zusammengefasst werden. Es ergeben sich also die gleichen Widerstandswerte oben und unten. Auch bei den Knoten K1 und K2 ergeben sich jeweils die gleichen Widerstandwerte oben wie unten. Mit den jeweils gleichen Verhältnissen der Widerstände bei K1, K2 und K3 lässt sich folgern, dass über die Widerstände $R_3$ zwischen K1 und K2 bzw. K2 und K3 kein Strom fließt. Diese tragen also nicht zum Gesamtwiderstand bei. In einem solchen Fall kann zwischen den relevanten Knoten für die Rechnung ein Kurzschluss oder eine offene Leitung frei gewählt werden. Im folgenden wird eine offene Leitung gewählt. Zusätzlich können die parallelen Stränge noch umsortiert werden.
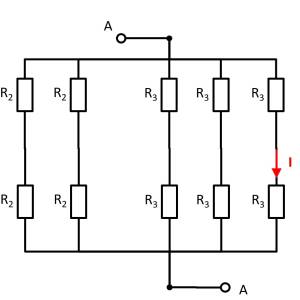
Damit ergibt sich:
\begin{align*} R_{ges} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) \quad && || \quad \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{ges} &= R_2 \quad && || \quad \frac{2}{3}\cdot R_3 \\ R_{ges} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} = \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Nun sei die Spannung von A nach B: $U_{AB}=U_0= 20 V$. Wie groß ist der Strom $I$?