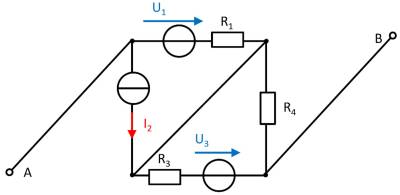
Aufgabe 4.5.2: Leerlaufspannung über Superposition (Klausuraufgabe, ca 12% einer 60minütigen Klausur, WS2020)
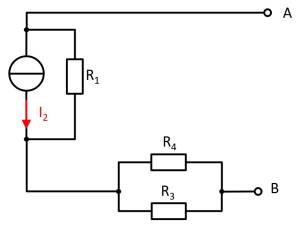
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$U_1=2 V$
$I_2=1 A$
$R_3=20 \Omega$
$U_3=8 V$
$R_4=10 \Omega$
Bestimmen Sie die Leerlaufspannung zwischen A und B mittels des Superpositionsprinzips.
- Wie sehen die Einzelschaltungen aus, durch denen die Wirkungen (Spannung zwischen A und B) der einzelnen Quellen berechenbar wird?
Durch welchen Ersatzwiderstand muss eine Strom- bzw. eine Spannungsquelle bei der Berechnung der einzelnen Wirkungen ersetzt werden? - Wo liegen bei der Einzelbetrachtung die Leerlaufspannungen an?
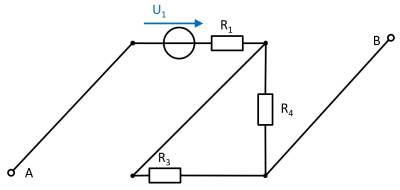
(Spannungs)Quelle $U_1$
- Stromquelle $I_2$ durch Kurzschluss ersetzen
- Spannungsquelle $U_3$ durch offene Leitung ersetzen
Werden die Komponenten verschoben, so ist die Schaltung besser zu verstehen:
Es zeigt sich, dass sich im Leerlauffall durch keinen Widerstand Strom fließt. Für die Wirkung gilt also: $U_{AB,1} = U_1$
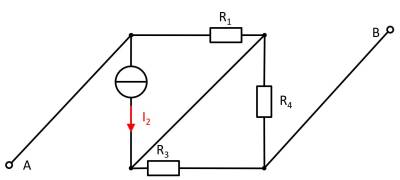
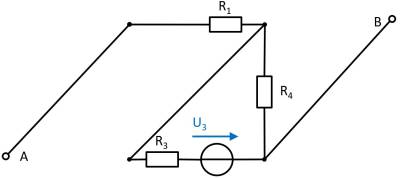
(Strom)Quelle $I_2$
- Spannungsquelle $U_1$ durch offene Leitung ersetzen
- Spannungsquelle $U_3$ durch offene Leitung ersetzen
Auch hier können Komponenten verschoben werden, um die Schaltung besser zu verstehen:
Hier erzeugt die Stromquelle $I_2$ am Widerstand $R_2$ die Spannung $U_{AB_2}$: $U_{AB,2} = - R_1 \cdot I_2$
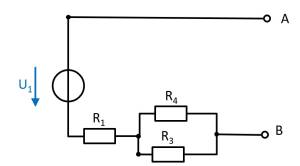
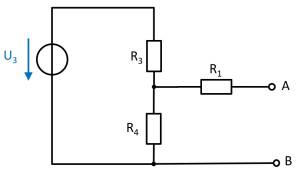
(Spannungs)Quelle $U_3$
- Spannungsquelle $U_1$ durch offene Leitung ersetzen
- Stromquelle $I_2$ durch Kurzschluss ersetzen
Ebenso wird auch hier die Schaltung verständlicher durch ein Verschieben der Komponenten:
In dieser Schaltung ergibt sich im Leerlauffall ein unbelasteter Spannungsteiler über $R_3$ und $R_4$. Über den Widerstand $R_1$ fließt im Leerlauf kein Strom.
Es ergibt sich:
\begin{align*} U_{AB,3} = \frac{R_4}{R_3 + R_4} \cdot U_3 \end{align*}
Resultierende Spannung
\begin{align*} U_{AB} &= U_1 - R_1 \cdot I_2 + \frac{R_4}{R_3 + R_4} \cdot U_3 \\ \end{align*}