Dies ist eine alte Version des Dokuments!
1. Grundlagen und Grundbegriffe
1.1 Physikalische Größen
Ziele
Nach dieser Lektion sollten Sie:
- die physikalischen Basisgrößen und die dazugehörigen SI-Einheiten kennen.
- die die wichtigsten Präfixe kennen. Sie können der jeweiligen Abkürzung eine Zehnerpotenz zuordnen (G, M, k, d, c, m, µ, n).
- in eine vorhandene Größengleichung gegebene Zahlenwerte und Einheiten einsetzen können. Daraus sollten Sie mit einem Taschenrechner das richtige Ergebnis berechnen können.
- die griechischen Buchstaben zuordnen können.
- immer mit Zahlenwert und Einheit rechnen.
- wissen, dass eine bezogene Größengleichung dimensionslos ist!
Basisgrößen
Kurzpräsentation der SI-Einheiten
| Basisgröße | Name | Einheitenzeichen | Definition |
|---|---|---|---|
| Zeit | Sekunde | s | Schwingung eines $Cä$-Atoms |
| Länge | Meter | m | über s und Lichtgeschwindigkeit |
| Stromstärke | Ampere | A | über s und Elementarladung |
| Masse | Kilogramm | kg | noch über kg-Prototyp |
| Temperatur | Kelvin | K | über Tripelpunkt des Wassers |
| Stoffmenge | Mol | mol | über Anzahl des $^{12}C$-Nuklids |
| Lichtstärke | Candela | cd | über vorgegebene Strahlstärke |
- Für die praktische Anwendung von physikalischen Naturgesetzen werden physikalische Größen in mathematische Beziehungen gesetzt.
- Es gibt Basisgrößen auf Basis des SI-Einheitensystems (frz. für Système International d'Unités), siehe unten
- Um die Basisgrößen quantitativ (quantum = lat. „wie groß“) zu bestimmen, werden physikalische Einheiten definiert, z.B. $Meter$ für die Länge
- In der Elektrotechnik sind die ersten drei Basisgrößen (vgl. Tabelle 1) besonders wichtig.
die Masse ist für die Darstellung von Energie und Leistung wichtig. - Jede physikalische Größe wird durch ein Produkt aus Zahlenwert und Einheit angegeben:
z.B. $I = 2 A$- Dies ist die Kurzform von $I = 2\cdot 1A$
- $I$ ist die physikalische Größe, hier: elektrische Stromstärke
- $\{I\} = 2 $ ist der Zahlenwert
- $ [I] = 1 A$ ist die (Maß-)Einheit, hier: Ampere
abgeleitete Größen, SI-Einheiten und Präfixe
- Neben den Basisgrößen gibt es auch davon abgeleitete Größen, z.B. $1{{m}\over{s}}$
- Bei Berechnungen sollten SI-Einheiten bevorzugt werden. Diese sind ohne Zahlenfaktor aus den Basisgrößen ableitbar.
- Die Druckeinheit Bar ($bar$) ist eine SI-Einheit
- ABER: Die veraltete Druckeinheit atmosphäre ($=1,013 bar$) ist keine SI-Einheit
- Um den Zahlenwert nicht zu groß oder zu klein werden zu lassen, ist es möglich einen dezimalen Faktor durch einen Präfix (Vorsatz) zu ersetzen. Diese sind in der Tabelle 2 aufgelistet.
Beispiel zur Potenzrechnung
physikalische Gleichungen
- Physikalische Gleichungen ermöglichen eine Verknüpfung von physikalischen Größen
- Es sind dabei zwei Arten von physikalische Gleichungen zu unterscheiden:
- Größengleichungen
- normierte Größengleichungen (auch bezogene Größengleichungen genannt)
Größengleichungen
Bei der überwiegenden Mehrheit der physikalische Gleichungen ergibt sich eine physikalische Einheit, welche ungleich $1$ ist.
Beispiel: Kraft $F = m \cdot a$ mit $[F] = kg \cdot {{m}\over{s^2}}$
- Bei Größengleichungen sollte immer eine Einheitenkontrolle durchgeführt werden
- Größengleichungen sollten allgemein bevorzugt werden
normierte Größengleichungen
Bei normierten Größengleichungen wird der Messwert oder Rechenwert einer Größengleichung durch einen Bezugswert dividiert. Es entsteht so eine dimensionslose Größe relativ zum Bezugswert.
Beispiel: Wirkungsgrad $\eta = {{P_{ab}}\over{P_{zu}}}$
Als Bezugswert werden häufig:
- Nennwerte (maximal zulässiger Wert im Dauerbetrieb) oder
- Maximalwerte (kurzfristig erreichbarer Maximalwert)
genutzt.
- Bei normierten Größengleichungen sollten sich die Einheiten immer auslöschen
Beispielrechnung für eine Größengleichungen
Gegeben sei ein Körper mit der Masse $m = 100kg$. Der Körper wird um den Weg $s=2m$ angehoben.Welche Arbeit wird dabei verrichtet?
physikalische Gleichung:
Arbeit = Kraft $\cdot$ Weg
$W = F \cdot s \quad\quad\quad\;$ mit $F=m \cdot g$
$W = m \cdot g \cdot s \quad\quad$ mit $m=100kg$, $s=2m$ und $g=9,81{{m}\over{s^2}}$
$W = 100kg \cdot 9,81{{m}\over{s^2}} \cdot 2m $
$W = 100\cdot 9,81 \cdot 2 \;\; \cdot \;\; kg \cdot {{m}\over{s^2}} \cdot m$
$W = 1962 \quad\quad \cdot \quad\quad\; \left( kg \cdot {{m}\over{s^2}} \right) \cdot m $
$W = 1962 Nm = 1962 J $
Buchstaben für physikalische Größen
| Groß- buchstaben | Klein- buchstaben | Name |
|---|---|---|
| $A$ | $\alpha$ | Alpha |
| $B$ | $\beta$ | Beta |
| $\Gamma$ | $\gamma$ | Gamma |
| $\Delta$ | $\delta$ | Delta |
| $E$ | $\epsilon$, $\varepsilon$ | Epsilon |
| $Z$ | $\zeta$ | Zeta |
| $H$ | $\eta$ | Eta |
| $\Theta$ | $\theta$, $\vartheta$ | Theta |
| $I$ | $\iota$ | Iota |
| $K$ | $\kappa$ | Kappa |
| $\Lambda$ | $\lambda$ | Lambda |
| $M$ | $\mu$ | My |
| Groß- buchstaben | Klein- buchstaben | Name |
|---|---|---|
| $N$ | $\nu$ | Ny |
| $\Xi$ | $\xi$ | Xi |
| $O$ | $\omicron$ | Omikron |
| $\Pi$ | $\pi$ | Pi |
| $R$ | $\rho$, $\varrho$ | Rho |
| $\Sigma$ | $\sigma$ | Sigma |
| $T$ | $\tau$ | Tau |
| $\Upsilon$ | $\upsilon$ | Ypsilon |
| $\Phi$ | $\phi$, $\varphi$ | Phi |
| $X$ | $\chi$ | Chi |
| $\Psi$ | $\psi$ | Psi |
| $\Omega$ | $\omega$ | Omega |
In der Physik und Elektrotechnik wurde häufig versucht für physikalische Größen dem (englischen) Begriff naheliegende Buchstaben zu finden.
So sind $C$ für Capacity, $Q$ für Quantity und $\varepsilon_0$ für die Electical Field Constant und weitere zu erklären.
Hierbei ist aber bereits schon zu sehen, dass das $C$ sowohl für die thermische Kapazität, als auch die elektrische Kapazität genutzt.
Das lateinische Alphabet hat für den Umfang der Physik nicht genug Buchstaben, um Konflikte zu vermeiden. Bei verschiedenen physikalischen Größen wird deswegen auf griechischen Buchstaben zurückgegriffen (siehe Tabelle 4).
Besonders in Elektrotechnik wird durch Groß-/Kleinschreibung unterschieden, ob es sich um
- eine zeitlich konstante (zeitunabhängige) Größe handelt,
z.B. die Periode $T$ - oder um eine zeitabhängige Größe handelt,
z.B. die Momentanspannung $u(t)$
Die relevanten griechischen Buchstaben für die Elektrotechnik werden in folgendem Video beschrieben.
Übungen
Aufgabe 1.1.1 Umrechnungen I - vorgerechnetes Beispiel zur Umrechnung von Einheiten
Aufgabe 1.1.2 Umrechnungen II
Rechnen Sie Schritt für Schritt folgende Werte um:
- Eine Fahrzeuggeschwindigkeit von 80 km/h in m/s
- Eine Energie von 60 Joule in kWh (1 Joule = 1 Watt*Sekunde)
- Die Anzahl elektrolytisch abgeschiedener, einfach positiv geladener Kupferionen von 1,2 Coulomb (ein Kupferion hat die Ladung von ca. $1,6 \cdot 10^{-19} C$)
- Aufgenommene Energie eines Kleinstverbrauchers, wenn dieser gleichmäßig in 10 Tagen 1 µW verbraucht
Aufgabe 1.1.3 Umrechnungen III
Rechnen Sie Schritt für Schritt folgende Werte um: Wie viele Minuten könnte eine ideale Batterie mit 10 kWh einen Verbraucher mit 3W betreiben?
Aufgabe 1.1.4 Umrechnungen IV
Rechnen Sie Schritt für Schritt folgende Werte um: Wie viel Energie verbraucht ein durchschnittlicher Haushalt am Tag, wenn er eine mittlere Leistung von 500 W aufnimmt? Wie viele Schokoriegel (je 2000 kJ) entspricht das?
1.2 Einführung in die Struktur der Materie
Ziele
Nach dieser Lektion sollten Sie:
- die Größe der Elementarladung kennen
Elementarladung
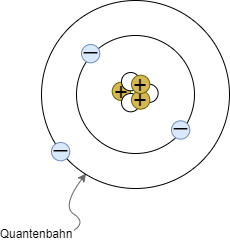
- Erklärung der Ladung anhand der Atommodelle nach Bohr und Sommerfeld (siehe Abbildung 1)
- Atome bestehen aus
- Atomkern (mit Protonen und Neutronen)
- Elektronenhülle
- Elektronen sind Träger der Elementarladung $|e|$
- Elementarladung $|e| = 1,6022\cdot 10^{-19} C$
- Proton ist der Gegenspieler, d.h. hat gegensätzliche Ladung
- Vorzeichen ist willkürlich gewählt:
- Elektronenladung: $-e$
- Protonenladung: $+e$
- alle Ladungen auf/in Körpern können nur als ganzzahlige Vielfache der Elementarladung auftreten
- Aufgrund des geringen Zahlenwerts von $e$ wird bei makroskopischer Betrachtung die Ladung als Kontinuum betrachtet
Leitfähigkeit
Leiter
Im Leiter sind Ladungsträger frei beweglich.
Beispiele:
- Metalle
- Plasma
Halbleiter
Im Halbleiter können Ladungsträger durch Wärme und Lichteinstrahlung generiert werden. Häufig ist bereits durch die Raumtemperatur eine geringe Bewegung der Elektronen möglich.
Beispiele:
- Silizium, Diamant
Isolator
Im Isolator sind Ladungsträger fest an den Atomhüllen gebunden.
Beispiele:
- viele Kunststoffe und Salze
Übungen
Aufgabe 1.2.1 Ladungen I
Wie viele Elektronen bilden die Ladung von einem Coulomb?
Aufgabe 1.2.2 Ladungen II
Ein Luftballon hat auf der Oberfläche eine Ladung von $Q=7nC$. Wie viele Elektronen sind zusätzlich auf dem Luftballon?
1.3 Effekte des elektrischen Stroms
Ziele
Nach dieser Lektion sollten Sie:
- wissen, dass zwischen Ladungen Kräfte wirken.
- das Coulombsche Gesetz kennen und anwenden können.
- Welche Effekte des elektrischen Stroms kennen Sie?
erste Näherung an die el. Ladung
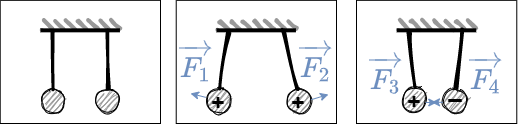
- erster Versuch (siehe Abbildung 2):
- zwei Ladungen ($Q_1$ und $Q_2$) sind im Abstand $r$ aufgehängt
- Ladungen werden durch Hochspannungsquelle erzeugt und auf die beiden Probekörper übertragen
- Ergebnis
- Probekörper mit gleichen Ladungen versehen $\rightarrow$ Abstoßung
- Probekörper mit Ladungen unterschiedlichen Vorzeichens versehen $\rightarrow$ Anziehung
- Erkenntnisse
- Die Kräfte können nicht mechanisch erklärt werden
- Es scheint zwei unterschiedliche Arten von Ladungen zu existieren. $\rightarrow$ positive (+) und negative (-) Ladung
Coulomb-Kraft
Aufbau für eigene Versuche
Nehmen Sie eine Ladung ($+1nC$) und positionieren Sie diese. Messen Sie das Feld über eine Probeladung (einen Sensor) aus.
Versuch zum Coulomb'schen Gesetz
- Qualitative Untersuchung mittels zweitem Versuch
- zwei Ladungen ($Q_1$ und $Q_2$) im Abstand $r$
- zusätzlich Messung der Kraft $F_C$ (z.B. über Federwaage)
- Versuch ergibt:
- Kraft steigt linear bei größerer Ladung $Q_1$ oder $Q_2$
$ F_C \sim Q_1$ und $ F_C \sim Q_2$ - Kraft fällt quadratisch bei größerem Abstand $r$
$ F_C \sim {1 \over {r^2}}$ - mit einem Proportionalitätsfaktor $a$:
$ F_C = a \cdot {{Q_1 \cdot Q_2} \over {r^2}}$
- Proportionalitätsfaktor $a$
- Der Proportionalitätsfaktor $a$ wird so definiert, dass sich in der Elektrodynamik einfachere Beziehungen entstehen.
- $a$ wird damit zu:
$a = {{1} \over {4\pi\cdot\varepsilon}}$ - $\varepsilon_0$ ist die Elektrische Feldkonstante. Im Vakuum wird $\varepsilon_0 = \varepsilon$
- Die Formel ähnelt derjenigen der Gravitationskraft: $F_G = {\gamma \cdot {{m_1 \cdot m_2} \over {r^2}}}$
Merke:
Die Coulombkraft (im Vakuum) lässt sich berechnen über$\boxed{ F_C = {{{1} \over {4\pi\cdot\varepsilon_0}} \cdot {{Q_1 \cdot Q_2} \over {r^2}}}}$
mit $\varepsilon_0 = 8,85 \cdot 10^{-12} \cdot {{C^2 \over {m^2\cdot N}}} = 8,85 \cdot 10^{-12} \cdot {{As} \over {Vm}}$
1.4 Ladung und Strom
Ziele
Nach dieser Lektion sollten Sie:
- die technische Stromrichtung und den Stromfluss der Elektronen unterscheiden können
- Katode und Anode bei Komponenten bestimmen können
- die Definition von Strom anwenden können
Die elektrische Ladung
- Aus vorherigen Versuchen ist klar, dass es zwei Ladungstypen gibt. In Materie sind diese:
- (+) $\rightarrow$ Überschuss an positiven Ladungen
- (-) $\rightarrow$ Überschuss an negativen Ladungen
- weiterer Versuch:
- (+) und (-) werden durch einen Leiter verbunden
- $\rightarrow$ Elektronen wandern von (-)-Pol zum (+)-Pol
- $\rightarrow$ elektrischer Strom
qualitative Betrachtung
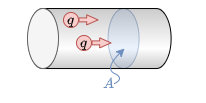
- In dem Gedankenexperiment sei folgendes gegeben (siehe Abbildung 3):
- der oben genannte Leiter mit einem Kontrollquerschnitt $A$ senkrecht zum Leiter
- die Ladungsmenge $\Delta Q = n \cdot e$, welche in einer bestimmten Zeitdauer $\Delta t$, die Fläche $A$ durchschreiten
- Bei einem gleichmäßiger Ladungstransport über längere Zeit, also Gleichstrom (engl. DC für Direct Current), gilt:
- Die Menge der Ladungen pro Zeit welche die Fläche durchfließen ist konstant:
${{\Delta Q} \over {\Delta t}} = konst. = I$ - $I$ bezeichnet hier die Stärke des Gleichstroms
- Die Einheit von $I$ ist die SI-Einheit Ampere: $1 A = {{1 C}\over{1 s}}$ . Damit gilt für die Einheit Coulomb $1 C = 1 A\cdot s$
Definition der Stromstärke
Es fließt der Strom von $1 A$, wenn in $1 s$ eine Ladungsmenge von $1 C$ durch den Leiterquerschnitt transportiert wird.Vor 2019: Es fließt der Strom von $1 A$, wenn zwei parallele Leiter von je $1m$ Länge im Abstand von $1m$ eine Kraft von $F_C = 0,2\cdot 10^{-6} N$ aneinander ausüben.
Merke:
Ein elektrischer Strom ist die gerichtete Bewegung von freien, elektrischen Ladungsträgern.Festlegung der Stromrichtung
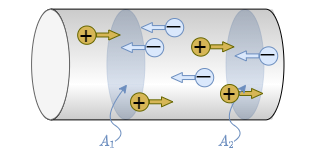
Ein Ladungstransport kann stattfinden durch (Abbildung 4):
- negative Ladungsträger $\color{midnightBlue}{\Delta Q_n}$ (z.B. Elektronen in einem metallischen Leiter)
- positive Ladungsträger $\color{brown}{\Delta Q_p}$ (z.B. bestimmte Halbleitermaterialien oder in elektrochemische Zellen)
- positive und negative Ladungsträger (z.B. bestimmte Halbleitermaterialien, Plasma)
Die gesamte transportierte Ladung beträgt $\Delta Q = \color{brown}{\Delta Q_p} - \color{midnightBlue}{\Delta Q_n} = n_p \cdot e - n_n \cdot (-e)$
$\rightarrow$ Die Stromrichtung muss unabhängig von der Bewegungsrichtung der elektrischen Ladungsträger festgelegt werden.
Definition der Stromrichtung (nach DIN5489)
Der Strom in einem Leiter von einer Querschnittsfläche $A_1$ zu einer Querschnittsfläche $A_2$ wird positiv gerechnet, wenn sich:- positive Ladungsträger von $A_1$ nach $A_2$ bewegen, bzw.
- negative Ladungsträger von $A_2$ nach $A_1$ bewegen.
Die Stromrichtung (bzw. technische Stromrichtung) ist der Richtungssinn des positiven Stroms, also der positiven Ladungsträger.
Definition der Elektroden (nach DIN5489)
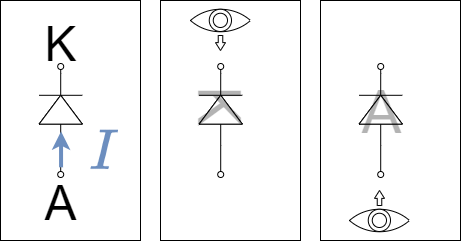
Als Elektrode ist bezeichnet man einen Anschluss einer elektrischen Komponente. In der Regel sind Elektroden dadurch gekennzeichnet, dass ein Materialwechsel stattfindet (z.B. Metall->Halbleiter, Metall->Flüssigkeit)- Anode: Elektrode an welcher der Strom in das Bauteil eintritt
- Kathode: Elektrode an welcher der Strom in das Bauteil austritt.
Als Eselsbrücke kann man sich den Aufbau, Form und Elektroden der Diode merken (siehe Abbildung 5).
Übungen
Aufgabe 1.4.1 Ermittlung des Stroms aus der Ladung pro Zeit
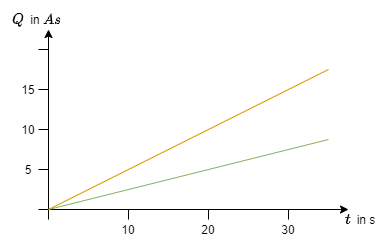
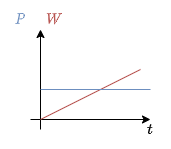
Es sei der Ladungsgewinn pro Zeit an einem Objekt gegeben.
- Ermitteln Sie aus nebenstehendem Diagramm (siehe Abbildung 6) die Ströme und zeichnen Sie diese in das Diagramm ein.
- Wie könnte bei nicht linearer Änderung der Ladungsmenge am Objekt vorgegangen werden?
Aufgabe 1.4.2 Elektronenfluss
Wie viele Elektronen treten durch einen Kontrollquerschnitt eines metallischen Leiters, wenn $4,5s$ lang der Strom von $40mA$ fließt?
1.5 Spannung, Potential und Energie
Ziele
Nach dieser Lektion sollten Sie:
- den Energiegewinn einer Ladung bei überwinden einer Spannugsdifferenz ermitteln können
energetischer Ansatz
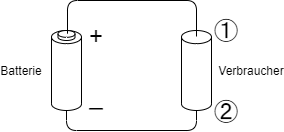
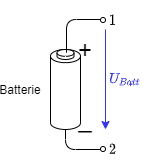
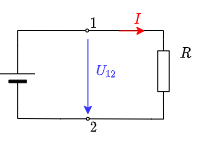
Gegeben sei ein elektrischer Leiter („Verbraucher“) an einer Batterie (siehe Abbildung 7)
- $\rightarrow$ Strom fließt
- Ähnlich wie beim Transport einer Masse im Schwerefeld wird beim Transport der Ladung im „Spannungsfeld“ Energie nötig
- Das konkrete elektrische Feld werden wir später im Semester betrachten
- Eine Punktladung $q$ wird von Elektrode ① zur Elektrode ② bewegt
Die ähnelt einer bewegten Massepunkt im Schwerefeld. - $\rightarrow$ es findet ein Energieumsatz statt
- Der Energieumsatz ist proportional der transportierten Ladungsmenge $q$
- In vielen Fällen ist den „energetischen Weg“ von ① zu ② ladungsunabhängig zu charakterisieren:
$\boxed{{{W_{1,2}}\over{q}} = U_{1,2}}$ - Im englischen Sprachraum wird häufig $V$ (für Voltage) als Bezeichnung der Größe genutzt:
z.B.- $VCC = 5V$ : Spannungsversorgung eines IC (Voltage Common Collector),
- $V_{S+} = 15V$ : Spannungsversorgung eines Operationsverstärkers (Voltage Supply plus).
Vergleich Mechanik zu Elektrik
Elektrik
Potential
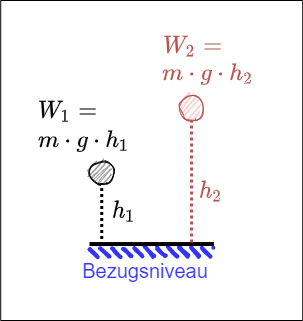
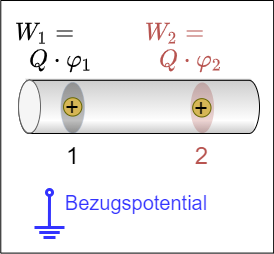
Das Potential $\varphi$ wird immer festgelegt relativ zu einem Bezugspunkt.
Üblich ist:
- Erdpotential (Erde, Masse, Ground)
- unendlich entfernter Punkt
Zur Verschiebung der Ladung muss die Potentialtifferenz überwunden werden. Die Potentialdifferenz ist unabhängig vom Bezugspotential. $\boxed{\Delta W_{1,2} = W_1 - W_2 = Q \cdot \varphi_1 - Q \cdot \varphi_2 = Q \cdot (\varphi_1 - \varphi_2)}$
Daraus ergibt sich:
$\boxed{{\Delta W_{1,2} \over {Q}} = \varphi_1 - \varphi_2 = U_{1,2}}$
Merke:
- Spannung ist immer eine Potentialdifferenz.
- Die Einheit der Spannung ist Volt: $1 V$
Definition der Spannung
Eine Spannung von $1 V$ liegt dann zwischen zwei Punkten an, wenn eine Ladung von $1 C$ zwischen diesen beiden Punkten eine Energieänderung von $1J = 1Nm$ erfährt.Aus $W=U \cdot Q$ ergibt sich auch die Einheit: $1Nm = 1V\cdot As \rightarrow 1V = 1{{Nm}\over{As}}$
Spannung zwischen zwei Punkten
Für die Spannung zwischen zwei Punkten ergibt sich mit dem bisherigen Kenntnissen folgende Definition:
$U_{12} = \varphi_1 - \varphi_2 = -U_{21} = - (\varphi_2 - \varphi_1)$
Es ist also im Folgenden stets die Reihenfolge der Indizes zu beachten.
Definition der konventionellen Richtung der Spannung (nacg DIN5489)
Die Spannung von $U_{12}$ entlang einem Weg von Punkt ① nach ② wird positiv, wenn das Potential in ① größer ist als das Potential in ②.Übungen
Aufgabe 1.5.1 Richtung der Spannung
Geben Sie für die Spannungen $U_{Batt}$, $U_{12}$ und $U_{21}$ in Abbildung 10 an, ob diese nach der Spannungsdefinition positiv oder negativ sind.
1.6 Widerstand und Leitwert
Ziele
Nach dieser Lektion sollten Sie:
- das ohmsche Gesetz kennen und anwenden können.
- den Widerstand aus dem spezifischen Widerstand berechnen können.
- den Leitwert aus dem Widerstand bzw. der spezifischen Leitfähigkeit ermitteln können.
- wissen, welche Fälle der Temperaturabhängigkeiten unterschieden und wie diese benannt werden.
- den Widerstand bei unterschiedlichen Temperaturen berechnen können.
- wissen, dass es verschiedene Bauformen gibt und, dass die physikalische Größe des Widerstands nicht von der geometrischen Größe abhängt
Stromfluss erfordert im allgemeinen Energieaufwand. Diese Energie wird dem elektrischen Stromkreis entzogen und in der Regel in Wärme gewandelt. Der Grund dafür ist der Widerstand des Leiters.
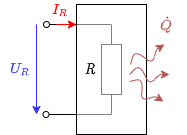
Ein Widerstand ist ein elektrisches Bauteil mit zwei Anschlüssen (bzw. Klemmen). Bauteile mit zwei Anschlüssen werden als Zweipol oder Eintor bezeichnet (Abbildung 11). Im zweiten Semester werden auch Vierpole bzw. Zweitore dazukommen.
Im Allgemeinen ist die Ursache-Wirkung-Beziehung so, dass eine angelegte Spannung am Widerstand den Stromfluss erzeugt. Es gilt aber auch die Umgekehrte Beziehung: Sobald ein elektrischer Strom über einen Widerstand fließt, wird ein Spannungsabfall am Widerstand erzeugt.
In der Elektrotechnik werden in den Schaltbildern mit idealisierten Komponenten gearbeitet. Dabei wird der Widerstand der Zuleitungen entweder vernachlässigt - sofern dieser sehr klein zu allen anderen Widerstandswerten ist - oder durch einen separaten Widerstand eingezeichnet.
Linearität von Widerständen
Lineare Widerstände
Abb. 12: lineare Widerstände im U-I-Diagramm
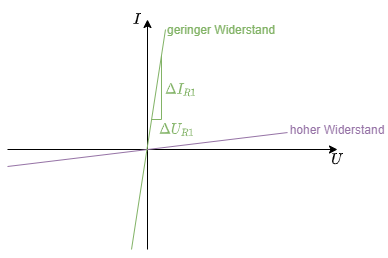
- Bei linearen Widerständen ist der Widerstandswert $R={{U_R}\over{I_R}}=const.$ und damit unabhängig von $U_R$
- Es ergibt sich das ohmsche Gesetz:
$\boxed{R={{U_R}\over{I_R}}}$ mit der Einheit $[R]={{[U_R]}\over{[I_R]}}= 1{{V}\over{A}}= 1\Omega$ - In Abbildung 12 lässt sich der Wert $R$ aus dem Verlauf der Geraden ablesen $R={{\Delta U_R}\over{\Delta I_R}}$
- Der Reziprokwert (Kehrwert) des Widerstands wird Leitwert genannt: $G={{1}\over{R}}$ mit der Einheit $1 S$ (Siemens). Dieser Wert ist im $U$-$I$-Diagramm als Steigung zu sehen.
Nichtlineare Widerstände
Abb. 13: nichtlineare Widerstände im U-I Diagramm
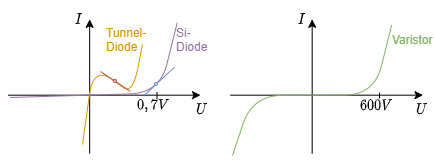
- Der Punkt im $U$-$I$-Diagramm, welcher in einem System eingenommen wird, nennt sich Arbeitspunkt oder Betriebspunkt. Im Abbildung 13 sind im linken Diagramm jeweils ein Arbeitspunkt mit einem Kreis markiert.
- Bei nichtlinearen Widerständen ist der Widerstandswert $R={{U_R}\over{I_R(U_R)}}=f(U_R)$. Dieser Widerstandswert ist vom Arbeitspunkt abhängig.
- Häufig sind kleine Änderungen um den Arbeitspunkt interessant (z.B. bei kleinen Störungen von Lastmaschinen). Hierfür wird der differentielle Widerstand $r$ (auch dynamischer Widerstand) ermittelt:
$\boxed{r={{dU_R}\over{dI_R}}\approx{{\Delta U_R}\over{\Delta I_R}}}$ mit der Einheit $[R]=1\Omega$ - Wie beim Widerstand $R$, ist auch beim differentiellen Widerstand $r$ der Reziprokwert der differentieller Leitwert $g$.
- In Abbildung 13 lässt sich der differentieller Leitwert $g$ aus der Steigung der Geraden in jedem Punkt ablesen $g={{dI_R}\over{dU_R}}$
Widerstand als Materialeigenschaft
Anschauliche Erklärung zum spezifischer Widerstand
Der Widerstandwert lässt sich auch über die Geometrie des Widerstands herleiten. Dazu kann ein Experiment mit unterschiedlich geformten Widerständen durchgeführt werden. Dabei lässt sich feststellen:
- der Widerstandswert $R$ steigt proportional mit der Länge $l$, die der Strom zurücklegen muss: $R \sim l$
- der Widerstandswert $R$ fällt umgekehrt proportional mit der Querschnittsfläche $A$ durch welche der Strom durchtritt: $R \sim {{1}\over{A}}$
- der Widerstandswert $R$ ist abhängig vom Material (Tabelle 6)
- damit erhält man:
$R \sim {{l}\over{A}}$
| Material | $\rho$ in ${{\Omega\cdot {mm^2}}\over{m}}$ |
|---|---|
| Silber | $1,59\cdot 10^{-2}$ |
| Kupfer | $1,79\cdot 10^{-2}$ |
| Aluminium | $2,78\cdot 10^{-2}$ |
| Gold | $2,2\cdot 10^{-2}$ |
| Blei | $2,1\cdot 10^{-1}$ |
| Graphit | $8\cdot 10^{0}$ |
| Akkusäure (Bleiakku) | $1,5\cdot 10^4$ |
| Blut | $1,6\cdot 10^{6}$ |
| (Leitungs)Wasser | $2 \cdot 10^{7}$ |
| Papier | $1\cdot 10^{15} ... 1\cdot 10^{17}$ |
Merke:
Der Widerstand lässt sich berechnen über$\boxed{R = \rho \cdot {{l}\over{A}} } $
- $\rho$ ist der materialabhängige, spezifische Widerstand mit der Einheit: $[\rho]={{[R]\cdot[A]}\over{l}}=1{{\Omega\cdot m^{\not{2}}}\over{\not{m}}}=1 \Omega\cdot m$
- Häufig wird statt $1 \Omega\cdot m$ die Einheit $1 {{\Omega\cdot {mm^2}}\over{m}}$ genutzt. Es gilt: $1 {{\Omega\cdot {mm^2}}\over{m}}= 10^{-6} \Omega m$
- Es existiert auch ein spezifischer Leitwert $\kappa$, gegeben über den Leitwert $G$ : $G= \kappa \cdot {{A}\over{l}}$
- Der spezifische Leitwert $\kappa$ ist der Kehrwert des spezifischem Widerstands $\rho$: $\kappa$
Temperaturabhängigkeit von Widerständen
Erklärung der Temperaturabhängigkeit von Widerständen
Der Widerstandswert wird - neben den bisher genannten Einflüssen von Geometrie und Material - auch von andere von anderen Effekten beeinflusst. Diese sind z.B.:
- Wärme (thermoresistiver Effekt, z.B. im Widerstandsthermometer)
- Licht (photoresistiver Effent z.B. im Bauteil Photowiderstand)
- Magnetfeld (magnetoresistiver Effekt z.B. in Festplatten)
- Druck (piezoresistiver Effekt z.B. Reifendrucksensor)
- chemische Umgebung (chemoresistiver Effekt z.B. chemische Analyse der Atemluft)
Um diese Einflüsse in Formel zu fassen, wird häufig auf das mathematische Hilfsmittel der Taylorreihe zurückgegriffen. Diese soll hier praktisch anhand des thermoresistives Effekts genutzt werden. Der thermoresistive Effekt, bzw. die Temperaturabhängigkeit von Widerständen ist eines der häufigsten (Stör-)Einflüssen in Bauteilen.
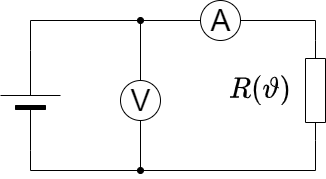
Der Ausgangspunkt für soll hier auch wieder ein Experiment sein. Es soll der ohmsche Widerstand in Abhängigkeit der Temperatur bestimmt werden. Dazu wird der Widerstand mittels einer Spannungsquelle, einem Voltmeter (Spannungsmessgerät) und einem Amperemeter (Strommessgerät) ermittelt und die Temperatur geändert (Abbildung 14).
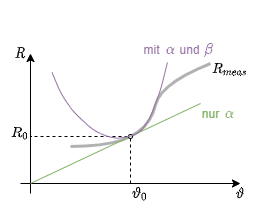
Es ergibt sich ein Verlauf des Widerstands $R$ über die Temperatur $\vartheta$ wie in Abbildung 15 gezeigt. Diese werden in erster Näherung durch einen linearen Verlauf um einen Arbeitspunkt angenähert. Daraus ergibt sich:
$R(\vartheta) = R_0 + c\cdot (\vartheta - \vartheta_0)$
- Die Konstante wird hierbei ersetzt durch $c = R_0 \cdot \alpha$
- $\alpha$ ist hierbei der lineare Widerstands-Temperaturkoeffizient mit der Einheit: $ [\alpha] = {{1}\over{[\vartheta]}} = {{1}\over{K}} $
- Neben dem linearen Term ist es auch möglich mit höherem Exponenten des Temperatureinflusses die Genauigkeit der Berechnung von $R(\vartheta)$ erhöhen. Dieser Ansatz wir in Mathematik unter Potenzreihe nochmals detaillierter betrachtet
- Diese Widerstands-Temperaturkoeffizienten werden mit griechischen Buchstaben beschrieben: $\alpha$, $\beta$, $\gamma$, …
Merke:
Die Temperaturabhängigkeit eines Widerstands wird über folgende Gleichung beschrieben: $\boxed{ R(\vartheta) = R_0 (1 + \alpha \cdot (\vartheta - \vartheta_0) + \beta \cdot (\vartheta - \vartheta_0)^2 + \gamma \cdot (\vartheta - \vartheta_0)^3 + ...}$
Dabei sind:
- $\alpha$ der (lineare) Widerstands-Temperaturkoeffizient mit der Einheit: $ [\alpha] = {{1}\over{K}} $
- $\beta$ der (quadratische) Widerstands-Temperaturkoeffizient mit der Einheit: $ [\beta] = {{1}\over{K^2}} $
- $\gamma$ der Widerstands-Temperaturkoeffizient mit der Einheit: $ [\gamma] = {{1}\over{K^3}} $
- $\vartheta_0$ die vorgegebene Bezugstemperatur (oder Referenztemperatur), meist $0°C$ oder $25°C$
Je weiter der Temperaturbereich von der Bezugstemperatur abweicht, desto mehr Temperaturkoeffizient sind notwendig, um den tatsächlichen Verlauf nachzubilden (Abbildung 16).
Ausblick
Neben der Angabe der Parameter $\alpha$,$\beta$, … ist gelegentlich auch die Angabe von $R_{25}$ und $B_{25}$ zu finden. Hierbei handelt es sich um eine andere Variante an Näherung, welche sich auf die Temperatur von $25°C$ bezieht. Diese beruht auf der Arrhenius-Gleichung, welche in der Chemie die Reaktionskinetik mit der Temperatur verbindet. Bei NTCs verknüpft die Arrhenius-Gleichung die Hemmung der Ladungsträgerbewegung durch Gittervibrationen mit der Temperatur $R(T) \sim e^{{B}\over{T}} $Auch hier lässt sich wieder eine Reihen-Entwicklung ansetzen: $R(T) \sim e^{A + {{B}\over{T}} + {{C}\over{T^2}} + ...}$
Häufig wird aber nur $B$ angegeben.
Durch Verhältnisbildung einer beliebigen Temperatur $T$ und $T_{25}=298,15 K$ ($\hat{=} 25°C$) ergibt sich:
${{R(T)}\over{R_{25}}} = {{exp \left({{B}\over{T}}\right)} \over {exp \left({{B}\over{298,15 K}}\right)}} $ mit $R_{25}=R(T_{25})$
Damit lässt sich die endgültige Formel ermitteln:
$R(T) = R_{25} \cdot exp \left( B_{25} \cdot \left({{1}\over{T}} - {{1}\over{298,15 K}} \right) \right) $
Arten von temperaturabhängigen Widerständen
Neben der Temperaturabhängigkeit als Störeinfluss gibt es auch Bauteile, welche bewusst auf eine bestimmten Temperatureinfluss gezüchtet worden sind. Diese werden als Thermistor (Kofferwort aus: thermally-sensitive resistor) bezeichnet. Die Thermistoren teilen sich in prinzipiell Heißleiter und Kaltleiter auf.
Eine Sonderform sind Materialien, welche in explizit auf eine minimale Temperaturabhängigkeit optimiert wurden (z.B. Konstantan oder Isaohm).
Heißleiter
Abb. 17: Heißleiter im U-I-Diagramm
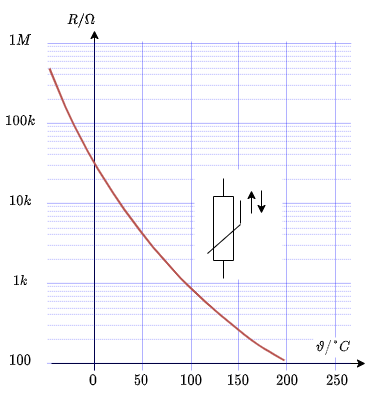
- Wie der Name vermuten lässt, hat der Heißleiter bei höheren Temperaturen einen geringeren Widerstand
- Ein Heißleiter wird auch NTC (engl. für negative temperature coefficient) genannt
- Beispiele dafür sind Halbleiter
- Anwendungen sind Einschaltstrombegrenzer und Temperatursensoren. Für den gewünschten Arbeitspunkt wird dabei ein dort stark nicht-linearer Verlauf gewählt (z.B. Fieberthermometer).
Kaltleiter
Abb. 18: Kaltleiter im U-I Diagramm
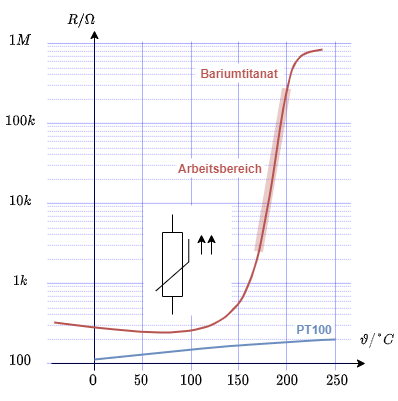
- Der Kaltleiter zeigt bei höheren Temperaturen einen höheren Widerstand
- Ein Kaltleiter wird auch PTC (engl. für positive temperature coefficient) genannt
- Beispiele dafür sind dotierte Halbleiter oder Metalle
- Anwendungen sind Temperatursensoren. Hierzu bieten sie häufig einen großen Temperaturbereich und gute Linearität (z.B. PT100 im Bereich von $-100°C$ bis $200°C$).
- Interaktives Beispiel zum Kaltleiter
Bauformen von Widerständen
Die Bauformen werden hier nicht näher erklärt. Es wird auf das rechtsstehende Video verwiesen.
Übungen
Aufgabe 1.6.1 vorgerechnetes Beispiel zum spezifischen Widerstand
Aufgabe 1.6.2 Widerstand eines Bleistift-Strichs
Es soll angenommen werden, dass eine weiche Bleistift-Mine zu 100% aus Graphit besteht. Wie groß ist der Widerstand einer $5cm$ langen und $0,2mm$ breiten Linie, wenn diese eine Höhe von $0,2\mu m$ hat?
Der spez. Widerstand ist über die Tabelle 6 gegeben.
Aufgabe 1.6.3 Widerstand einer Zylinderspule
Gegeben sei eine Zylinderspule in Form einer mehrlagigen Wicklung, wie sie z.B. auch in Motoren vorkommen können. Die Zylinderspule hat einen inneren Durchmesser von $d_i=70mm$ und einen äußeren Durchmesser von $d_a = 120mm$. Die Windungsanzahl beträgt $n_W=1350$ Windungen, der Drahtdurchmesser $d=2,0mm$ und die spezifische Leitfähigkeit des Drahtes $\kappa_{Cu}=56 \cdot 10^6 {{S}\over{m}}$.
Berechnen Sie zunächst die aufgewickelte Drahtlänge und im Anschluss den ohmschen Widerstand der gesamten Spule.
Aufgabe 1.6.4 Widerstand einer Zuleitung
Die Zuleitung zu einem Verbraucher soll ausgetauscht werden. Aufgrund der Anwendung muss der Leiterwiderstand gleich bleiben.
- Die alte Aluminium-Zuleitung hatte eine spezifische Leitfähigkeit $\kappa_{Al}=33\cdot 10^6 {{S}\over{m}}$ und einen Querschnitt $A_{Al}=115mm^2$
- Die neue Kupfer-Zuleitung hat eine spezifische Leitfähigkeit $\kappa_{Cu}=56\cdot 10^6 {{S}\over{m}}$
Welcher Leitungsquerschnitt $A_{Cu}$ muss gewählt werden ?
Aufgabe 1.6.5 Dehnmessstreifen
t.b.d.
Aufgabe 1.7.6: temperaturabhängiger Widerstand einer Wicklung (Klausuraufgabe, ca 6% einer 60minütigen Klausur, WS2020)
Auf dem Rotor eines Asynchronmotors sind die Wicklungen in Kupfer ausgelegt. Die Länge des Wickeldrahts ist 40 m. Der Durchmesser ist 0,4 mm.
Beim Start des Motors ist dieser gleichmäßig auf die Umgebungstemperatur von 20°C abgekühlt.
Im Betrieb haben die Wicklungen auf dem Rotor eine Temperatur von 90°C.
$\alpha_{Cu,20°C}=0,0039 \frac{1}{K}$
$\beta_{Cu,20°C}=0,6 \cdot 10^{-6} \frac{1}{K^2}$
$\rho_{Cu,20°C}=0,0178 \frac{\Omega mm^2}{m}$
Verwenden Sie sowohl den linearen als auch quadratischen Temperaturkoeffizienten! 1. Bestimmen Sie den Widerstand der Leitung für $T = 20°C$.
2. Welche Widerstandserhöhung $\Delta R$ ist zwischen $20°C$ und $90°C$ bei einer Wicklung festzustellen?
1.7 Leistung und Wirkungsgrad
Ziele
Nach dieser Lektion sollten Sie:
- die elektrische Leistung und Energie an einem Widerstand berechnen können.
Ermittlung der elektrischen Leistung im Gleichstrom-Stromkreis
Aus dem Kapitel 1.5 Spannung, Potential und Energie ist bekannt, dass eine Bewegung einer Ladung über eine Potentialdifferenz hinweg einer Änderung der Energie entspricht. Ladungstransport bedeutet also automatisch Energieaufwand. Häufig interessiert aber der Energieaufwand pro Zeiteinheit.
Die Energieaufwand pro Zeiteinheit stellt die Leistung dar:
$\boxed{P={{\Delta W}\over{\Delta t}}}$ mit der Einheit $[P]={{[W]}\over{[t]}}=1 {{J}\over{s}} = 1 {{Nm}\over{s}} = 1 V\cdot A = 1 W$
Für eine konstante Leistung $P$ und einer Anfangsenergie $W(t=0)=0$ gilt:
$\boxed{W=P \cdot t}$
Gelten die oben genannten Einschränkungen nicht, muss die erzeugte/benötigte Energie über ein Integral berechnet werden.
Neben dem Stromfluss von der Quelle zum Verbraucher (und zurück), fließt auch die Leistung von der Quelle zum Verbraucher.
Betrachtet man nur einen Gleichstrom-Stromkreis, so wird zwischen den Klemmen folgende Energie umgesetzt (siehe auch Abbildung 19 und Abbildung 20):
$W=U_{12}\cdot Q = U_{12} \cdot I \cdot t$
Damit ergibt sich für die Leistung (d.h. pro Zeiteinheit umgesetzte Energie):
$\boxed{P=U_{12} \cdot I}$ mit der Einheit $[P]= 1 V\cdot A = 1W \quad$ … $W$ steht hier für Watt.
Für ohmsche Widerstände gilt:
$\boxed{P=R\cdot I^2 = {{U_{12}^2}\over{R}}}$
Nenngrößen von ohmschen Verbrauchern
| Name der Nenngröße | physikalische Größe | Beschreibung |
|---|---|---|
| Nennleistung | $P_N$ | $P_N$ ist die im Dauerbetrieb zulässige Leistungsabgabe eines Geräts (Verbraucher oder Generator) |
| Nennstrom | $I_N$ | $I_N$ ist der im Betrieb mit Nennleistung auftretender Strom |
| Nennspannung | $U_N$ | $U_N$ ist der im Betrieb mit Nennleistung auftretender Spannung |
Wirkungsgrad
Die nutzbare (= nach außen abgegebene) $P_A$ Leistung ist immer kleiner als die zugeführte (eingehende) Leistung $P_E$. Die Differenz wird als Verlustleistung $P_V$ bezeichnet. Es gilt damit:
$P_E = P_A + P_V$
Anstelle der Verlustleistung $P_V$ wird häufig der Wirkungsgrad $\eta$ angegeben:
$\boxed{\eta = {{P_{A}}\over{P_{E}}}\overset{!}{<} 1}$
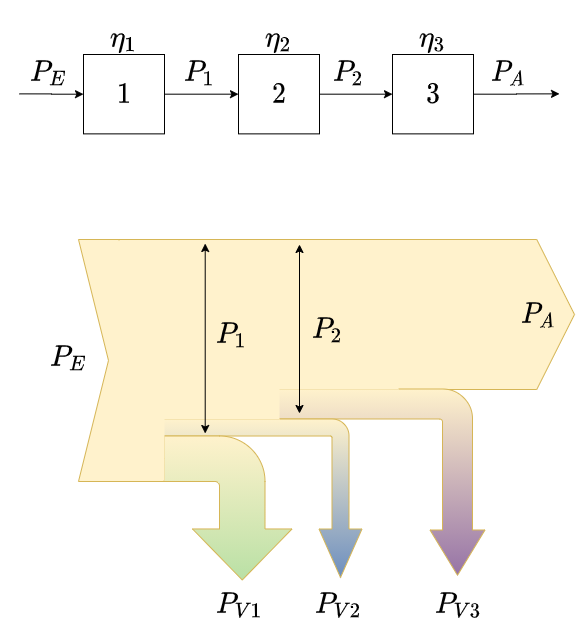
Bei hintereinandergeschalteten Systemen (siehe Abbildung 21) ergibt sich der Gesamtwiderstand über:
$\boxed{\eta = {{P_{A}}\over{P_{E}}} = {\not{P_{1}}\over{P_{E}}}\cdot {\not{P_{2}}\over \not{P_{1}}}\cdot {{P_{A}}\over \not{P_{2}}} = \eta_1 \cdot \eta_3 \cdot \eta_3}$
Übungen
Aufgabe 1.7.1 vorgerechnetes Beispiel zur elektrischen Leistung und Energie
Aufgabe 1.7.2 Leistung
Auf einer Platine wird ein SMD Widerstand zur Strommessung eingesetzt. Der Widerstandswert soll $R=0,2\Omega$ betragen, die Maximalleistung $P_N=250 mW$.
Welcher Strom kann höchstens gemessen werden?
Aufgabe 1.7.3 Verlustleistung und Wirkungsgrad I
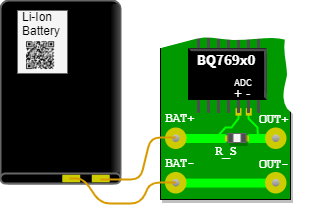
- Der Batteriemonitor BQ769x0 misst die Lade- und Entladeströme einer Lithium-Ionen-Batterie mittels der Spannung über einem Messwiderstand (eng. Shunt). In Abbildung 22 ist der Analog-Digital-Wandler ($ADC$) dieses Chips über die Platine am Shunt $R\_S$ angeschlossen. Durch den Shunt fließt der Entladestrom vom Batterieanschluss $BAT+$ zu $OUT+$ und über $OUT-$ zurück zu $BAT-$. Der Shunt soll so ausgelegt sein, dass die bipolaren Messsignale einen Spannungspegel im Bereich von $-0,20 V$ bis $+0,20 V$ haben. Der Analog-Digital-Wandler hat eine Auflösung von $15uV$. Anhand der Ströme kann die Ladung in der Batterie gezählt und damit der Ladezustand (SOC) ermittelt werden.
- Zeichnen Sie ein Ersatzschaltbild mit Spannungsquelle (Batterie), Messwiderstand und Lastwiderstand $R_L$. Zeichnen Sie auch die Messpannung und Lastspannung ein.
- Der Shunt soll einen Widerstandswert von $1m\Omega$ haben. Welche maximalen Lade-/Entladeströme sind noch messbar? Welche minimale Stromänderung ist messbar?
- Welche Verlustleistung wird im Extremfall am Shunt erzeugt?
- Nun soll der Wirkungsgrad berechnet werden
- Ermitteln Sie den Wirkungsgrad als Funktion von $R\_S$ und $R_L$. Beachten Sie, dass durch beide Widerstände der gleiche Strom fließt.
- Sonderaufgabe: Die Batterie soll eine Nominalspannung von $10V$ haben (3 Zellen) und der maximale Entladestrom soll fließen. Welchen Wirkungsgrad ergeben sich allein durch die Messung?
Aufgabe 1.7.4 Verlustleistung und Wirkungsgrad II
Eine Wasserpumpe ($\eta_P = 60\%$) besitzt einen elektromotorischem Antrieb ($\eta_M=90\%$). Die Pumpe soll je Minute $500l$ Wasser $12m$ hochpumpen.
- Welche Nennleistung muss der Motor haben?
- Welchen Strom nimmt der Motor am $230V$-Netz auf?
Weiterführendes
- Omega Tau Nr. 303 : Podcast mit einem Forscher der BTP über die Weiterentwicklung des SI Einheiten Systems