Dies ist eine alte Version des Dokuments!
3. Lineare Quellen und Zweipole
Aus dem Alltag ist bekannt, dass Batteriespannungen bei starker Belastung einbrechen. Dies zeigt sich zum Beispiel bei beim Drehen des Zündschlüssels im Winter: Die Belastung durch den Startermotor ist teilweise so groß, dass das Abblendlicht oder Radio kurzzeitig aussetzt.
Ein anderes Beispiel sind $1,5V$-Batterien: Wird eine solche Batterie durch ein Drahtstück kurzgeschlossen so fließt nicht soviel Strom, dass das Drahtstück glüht, sondern merklich weniger.
Es ist also sinnvoll hier das Konzept der idealen Spannungsquelle weiter zu entwickeln. Zusätzlich werden wir sehen, dass damit auch eine Möglichkeit eröffnet wird, kompliziertere Schaltungen umzuwandeln und zu vereinfachen.
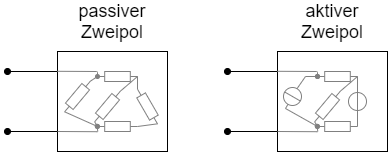
Zunächst soll der Begriff des Zweipols aus dem Kapitel Grundlagen und Grundbegriffe erweitert werden (Abbildung 1).
- Als passiver Zweipol wird im Folgenden ein Zweipol bezeichnet, welcher ausschließlich als Verbraucher wirkt. Damit gilt für den passiven Zweipol, dass die Strom-Spannungs-Kennlinie immer durch den Ursprung verläuft (siehe auch Kapiel Einfache Stromkreise)
- Aktive Zweipole hingegen wirken auch als Erzeuger elektrischer Energie. Damit verläuft die Strom-Spannungs-Kennlinie dort nicht durch den Ursprung. Aktive Zweipole enthalten immer mindestens eine Quelle (d.h. mindestens eine Strom- oder Spannungsquelle).
3.1 lineare Quellen
Ziele
Nach dieser Lektion sollten Sie:
- den Unterschied zwischen einer idealen und linearen Spannungs- bzw. Stromquelle beschreiben können.
- den Zusammenhang zwischen abgegebener Spannung, Quellenspannung $U_q$ und Innenwiderstand $R_i$ kennen und anwenden können.
- den Zusammenhang zwischen abgegebenem Strom, Quellenstrom $I_q$ und Innenleitwert $G_i$ kennen und anwenden können.
- anhand von Leerlaufspannung und Kurzschlussstrom den Spannungsverlauf der linearen (Spannungs-/Strom)quelle darstellen können.
- anhand zweier Strom/Spannungs-Messpunkte die Leerlaufspannung und den Kurzschlussstrom ermitteln können.
- den Grund für Dualität von Strom- und Spannungsquelle erklären können.
- eine lineare Stromquelle in eine lineare Spannungsquelle und umgekehrt umwandeln können.
praktisches Beispiel einer realitätsnahen Quelle
Für die ideale Spannungsquelle wurde definiert, dass diese unabhängig von der Last stets die gleiche Spannung liefert. In Abbildung 2 wird im Gegensatz dazu ein Beispiel einer „realitätsnahen“ Spannungsquelle als aktiven Zweipol dargestellt.
- Dieser aktiven Zweipol erzeugt bei offener Schaltung eine Spannung von $1,5V$ und einen Strom von $0A$.
- Wird nun ein Widerstand hinzugeschalten, so sinkt die Spannung, wohingegen der Strom steigt. Beispielsweise liegt am Widerstand von $2 \Omega$ eine Spannung von $1,2V$ an und ein Strom von $0,6A$ fließt.
- Über den äußeren Schalter können die Anschlüsse des aktiven Zweipols direkt miteinander verbunden werden. Dann fließt ein Strom von $3A$ bei einer Spannung von $0V$.
Diese Erkenntnis soll nun mit einigen Fachtermini beschrieben werden:
- Man spricht vom Leerlauf, wenn kein Strom aus einem aktiven Zweipol entnommen wird: $I_{LL}=0$.
Die Spannung entspricht der Leerlaufspannung $U=U_{LL}$ (englisch: OCV für Open Circuit Voltage).
Die Leerlaufleistung ist $P_{LL}=U_{LL} \cdot I_{LL} = 0$. - Man spricht vom Kurzschluss, wenn die Klemmen des Zweipols widerstandslos überbrückt sind. Der dann fließende Strom wird als Kurzschlussstrom bezeichnet $I=I_{KS}$.
Die Kurzschlussspannung ist $U_{KS}=0V$.
Auch die Kurzschlussleistung ist $P_{KS}=U_{KS} \cdot I_{KS} = 0$. - Im Bereich zwischen Leerlauf und Kurzschluss gibt der aktive Zweipol Leistung an einen angeschlossenen Verbraucher ab.
Wichtig: Wie in Folgenden zu sehen sein wird, können durch den Kurzschlussstrom im Inneren des Zweipols erhebliche Verlustleistung und damit eine große Abwärme entstehen. Dafür ist nicht jeder reelle Zweipol ausgelegt.
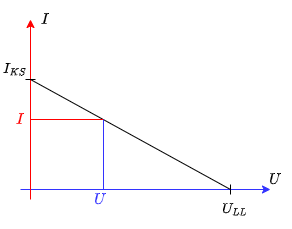
Interessant ist nun die Strom-Spannungs-Kennlinie der Schaltung in Abbildung 2. Diese ist in der Simulation unten zu sehen. Es ergibt sich ein linearer Verlauf (siehe Abbildung 3).
Rein mathematisch lässt sich der Verlauf über die Grundgleichung linearer Graphen mit dem y-Achsenabschnitt $I_{KS}$ und einer Steigung von $-{{I_{KS}}\over{U_{LL}}}$ darstellen:
\begin{align*} I = I_{KS} - {{I_{KS}}\over{U_{LL}}}\cdot U \tag{3.1.1} \end{align*}
Andererseits kann die Formel auch nach $U$ aufgelöst werden:
\begin{align*} U = U_{LL} - {{U_{LL}}\over{I_{KS}}}\cdot I \tag{3.1.2} \end{align*}
Merke:
Ergibt ein Zweipol einen linearen Verlauf zwischen $U_{LL}$ und $I_{KS}$ so wird er lineare Quelle genannt. Dieser Verlauf beschreibt in guter Näherung das Verhalten vieler realer Quellen. Häufig findet man synonym zum Begriff 'lineare Quelle' auch den Begriff 'reale (Spannungs)Quelle'. Dieser ist aber etwas irreführend, da es sich um ein vereinfachtes Modell für die Realität handelt.
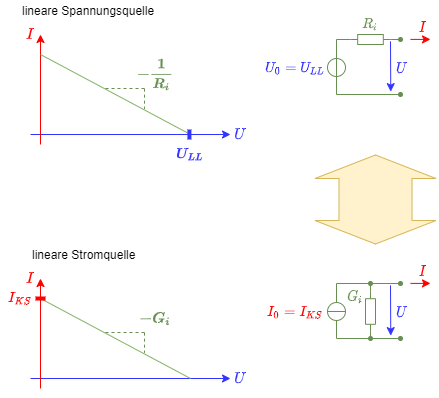
Wie sieht nun das Innere der linearen Quelle aus? In Abbildung 4 sind zwei mögliche, lineare Quellen dargestellt, die im Folgenden betrachtet werden.
lineare Spannungsquelle
Die lineare Spannungsquelle besteht aus einer Reihenschaltung einer idealen Spannungsquelle mit der Quellspannung $U_0$ (englisch: EMF für Elektro-Magnetic-Force) und dem Innenwiderstand $R_i$. Zur Ermittlung der Spannung außerhalb des aktiven Zweipols lässt sich das System als Spannungsteiler betrachten. Dabei gilt:
\begin{align*} U = U_0 - R_i \cdot I \end{align*}
Die Quellspannung $U_0$ der idealen Spannungsquelle ist an den Klemmen des Zweipols zu messen, wenn dieser unbelastet ist. Dann fließt kein Strom über den Innenwiderstand $R_i$ und es ergibt sich dort kein Spannungsabfall. Es gilt also: Die Quellenspannung ist gleich der Leerlaufspannung $U_0 = U_{LL}$.
\begin{align*} U = U_{LL} - R_i \cdot I \end{align*}
Wenn die äußere Spannung $U=0$ ist, handelt es sich um den Kurzschlussfall. In diesem Fall wird $0 = U_{LL} - R_i \cdot I_{KS}$ und umgeformt $R_i = {{U_{LL}}\over{I_{KS}}}$. Es ergibt sich also die Gleichung $(3.1.2)$: \begin{align*} U = U_{LL} - {{U_{LL}}\over{I_{KS}}} \cdot I \end{align*}
Ist das also der gesuchte Aufbau der linearen Quelle? Zur Überprüfung soll nun noch die zweite lineare Quelle betrachtet werden.
lineare Stromquelle
Die lineare Stromquelle besteht nun aus einer Parallelschaltung einer idealen Stromquelle mit dem Quellstrom $I_0$ und dem Innenwiderstand $R_i$, bzw. dem Innenleitwert $G_i = {{1}\over{R_i}}$. Zur Ermittlung der Spannung außerhalb des aktiven Zweipols lässt sich das System als Stromteiler betrachten. Dabei gilt:
\begin{align*} I = I_0 - G_i \cdot U \end{align*}
Hierbei kann der Quellstrom im Kurzschlussfall an den Klemmen gemessen werden. Es gilt also: $I_{KS}= I_0$
\begin{align*} I = I_{KS} - G_i \cdot U \end{align*}
Wenn der äußere Strom $I=0$ ist, handelt es sich um den Leerlauf-Fall. In diesem Fall wird $0 = I_{KS} - G_i \cdot U_{LL}$ und umgeformt $G_i = {{I_{KS}}\over{U_{LL}}}$.
Es ergibt sich also Gleichung $(3.1.1)$:
\begin{align*} I = I_{KS} - {{I_{KS}}\over{U_{LL}}} \cdot U \end{align*}
Es scheint also so, als ob die beiden linearen Quellen das gleiche beschreiben.
Dualität der linearen Quellen
Durch die vorherigen Berechnungen kamen wir zur interessanten Erkenntnis, dass sowohl die lineare Spannungsquelle, als auch die lineare Stromquelle das gleiche Ergebnis liefern. Es gilt: Für eine lineare Quelle kann als Ersatzschaltbild sowohl eine lineare Spannungsquelle als auch eine lineare Stromquelle angegeben werden! Wie bereits bei der Stern-Dreieck-Transformation wird damit nicht nur für eine Blackbox zwei Erklärungen geliefert. Auch hier können lineare Spannungsquellen in lineare lineare Stromquellen umgewandelt werden und umgekehrt.
Die Abbildung 5 stellt nochmals die beiden lineare Quellen und deren Kennlinien gegenüber:
- Die lineare Spannungsquelle ist gegeben durch die Quellspannung $U_0$, bzw. die Leerlaufspannung $U_{LL}$ und dem Innenwiderstand $R_i$
- Die lineare Stromquelle ist gegeben durch den Quellstrom $I_0$, bzw. den Kurzschlussstrom $I_{KS}$ und dem Innenleitwert $G_i$
Die Umwandlung geschieht nun so, dass sich die gleiche Kennlinie ergibt:
- Von linearer Spannungsquelle in lineare Stromquelle:
Gegeben: Quellspannung $U_0$, bzw. Leerlaufspannung $U_{LL}$, Innenwiderstand $R_i$
Gesucht: Quellstrom $I_0$, bzw. Kurzschlussstrom $I_{KS}$ , Innenleitwert $G_i$
$\boxed{I_{KS} = {{U_{LL}}\over{R_i}}}$ , $\boxed{G_i = {{1}\over{R_i}}}$ - Von linearer Stromquelle in lineare Spannungsquelle:
Gegeben: Quellstrom $I_0$, bzw. Kurzschlussstrom $I_{KS}$ , Innenleitwert $G_i$
Gesucht: Quellspannung $U_0$, bzw. Leerlaufspannung $U_{LL}$, Innenwiderstand $R_i$
$\boxed{U_{LL} = {{I_{KS}}\over{G_i}}}$ , $\boxed{R_i = {{1}\over{G_i}}}$
Arbeitspunkt einer realen Spannungsquelle
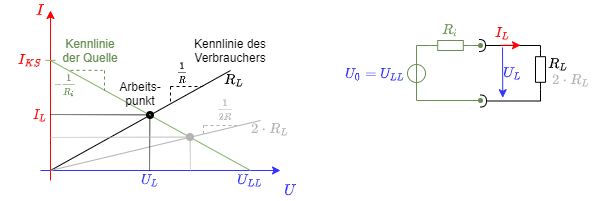
Abbildung 6 zeigt die Kennlinien der linearen Spannungsquelle (links) und eines ohmschen Widerstands (rechts). Dazu werden beide in der Simulation mit einem Testsystem verbunden: Im Fall der Quelle mit einem variablen, ohmschen Widerstand, im Fall des Verbrauchers mit einer variablen Quelle. Die so gebildeten Kennlinien wurden in vorherigen Kapitel beschrieben.
Aus beiden Kennlinien kann der Arbeitspunkt bestimmt werden. Dieser wird eingenommen, wenn beide die lineare Spannungsquelle mit dem ohmschen Widerstand verbunden werden (ohne die jeweiligen Testssysteme). In Abbildung 7 sind beide Kennlinien in einem Strom-Spannungsdiagramm gezeichnet. Der Schnittpunkt ist gerade der sich einstellende Arbeitspunkt. Wird der Lastwiderstand variiert, so ändert sich die Steigung umgekehrt proportional und ein neuer Arbeitspunkt stellt sich ein (hellgrau in der Abbildung).
Die Herleitung des Arbeitspunkts ist wird auch hier nochmals in einem Video erklärt.
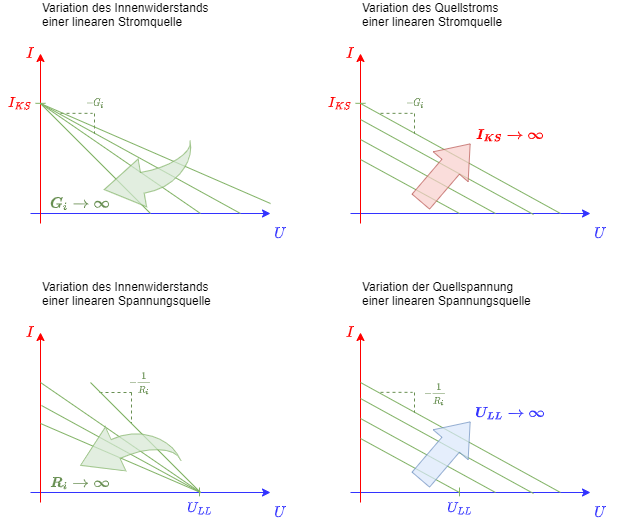
Es soll noch kurz auf die Variation der unterschiedlichen Quellparameter eingegangen werden.
Bei der linearen Stromquelle kann der Quellstrom $I_0$ und der Innenleitwert $G_i$ variiert werden. Daraus ergeben sich die Geradenscharen in Abbildung 8 oben. Der Quellstrom verschiebt die Geraden, wobei die Steigung konstant bleibt. Der Innenleitwert ändert nur die Steigung; es ergibt sich eine Geradenschar um den Schnittpunkt $I_0 = I_{KS}$.
Da eine ideale Stromquelle stets den Quellstrom liefern soll, ist ihr Innenleitwert $G_i=0$.
Bei der linearen Spannungsquelle kann die Quellspannung $U_0$ und der Innenwiderstand $R_i$ variiert werden. Daraus ergeben sich die Geradenscharen in Abbildung 8 unten. Die Quellspannung verschiebt die Geraden, wobei die Steigung konstant bleibt. Der Innenwiderstand ändert nur die Steigung; es ergibt sich eine Geradenschar um den Schnittpunkt $U_0 = U_{LL}$.
Da eine ideale Spannungsquelle stets die Quellspannung liefern soll, ist ihr Innenwiderstand $R_i=0$.
Aufgabe 3.1.1 Stromquelle in Spannungsquelle umwandeln
Aufgabe 3.1.2 Spannungsquelle in Stromquelle umwandeln
3.2 Umwandlung beliebiger linearer Zweipole
Ziele
Nach dieser Lektion sollten Sie:
- wissen, dass jede beliebige lineare Schaltung mit zwei Anschlüssen aus ohmschen Widerständen und Quellen als lineare Stromquelle bzw. lineare Spannungsquelle zu verstehen ist.
- die Quellen-Umwandlung bei komplizierteren Schaltungen mit mehreren Stromquellen bzw. Spannungsquellen anwenden können
- wissen, wie die Leerlaufspannung $U_{LL}$ und der Kurzschlusstrom $I_{KS}$) ermittelt werden können.
- die Parameter der Ersatzspannungsquelle (Innenwiderstand $R_i$ und Quellenspannung $U_q$) einer beliebigen linearen Schaltung berechnen können.
- die grafische Interpretation von Spannung und Strom am linearen Zweipol in Form einer Kennlinie verstehen und zeichnen können.
In Abbildung 5 ist zu sehen, dass der durch das Ohmmeter (Widerstandsmessgerät) gemessene Innenwiderstand der linearen Stromquelle genau gleich dem der linearen Spannungsquelle ist.
Betrachtet man die Eigenschaften des Ohmmeters in der Simulation, stellt man fest, dass dort ein Messstrom zur Ermittlung des Widerstandswerts genutzt wird. Dieses Konzept wird im 2. Semester noch Teil der Elektrotechniklabor-Versuchs zu Widerständen sein.
Jedoch wird hier ein sehr großer Messstrom von $1A$ verwendet. Dieser könnte in realen Aufbauten zu hohen Spannungen bzw. zur Zerstörung von Komponenten führen.
Warum ist dieser dennoch in der Simulation so hoch gewählt? Stellen Sie bei beiden linearen Quellen den Messstrom auf (realistischere) $1mA$. Was fällt dabei auf?
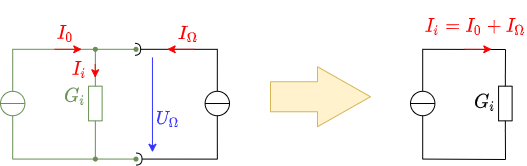
Die Schaltung in Abbildung 10 zeigt diese Schaltung nochmals. Das Ohmmeter ist durch eine Stromquelle und ein Voltmeter ersetzt, da im Folgenden nur die elektrischen Eigenschaften wichtig sind. In diesem Aufbau zeigt sich, dass der Strom durch $G_i$ gerade durch $I_i = I_0 + I_\Omega$ gegeben ist (Knotensatz). Die beiden Quellen in der Schaltung lassen sich also reduzieren.
Damit sollte die Situation mit einem Messstrom mit $1mA$ deutlich werden. Die Spannung am Widerstand ist nun durch $U_\Omega = R \cdot (I_0 + I_\Omega)$. Nur wenn $I_\Omega$ sehr groß ist, wird $I_0$ vernachlässigbar. Der Strom eines herkömmlichen Ohmmeters kann dies nicht bei jeder Messung gewährleisten.
Merke:
Sollen Widerstände in einer Schaltung gemessen werden, so muss mindestens ein Anschluss des Widerstands aus der Schaltung gelöst werden. Ansonsten können weitere Quellen oder Widerstände das Messergebnis verfälschen.komplexeres Beispiel
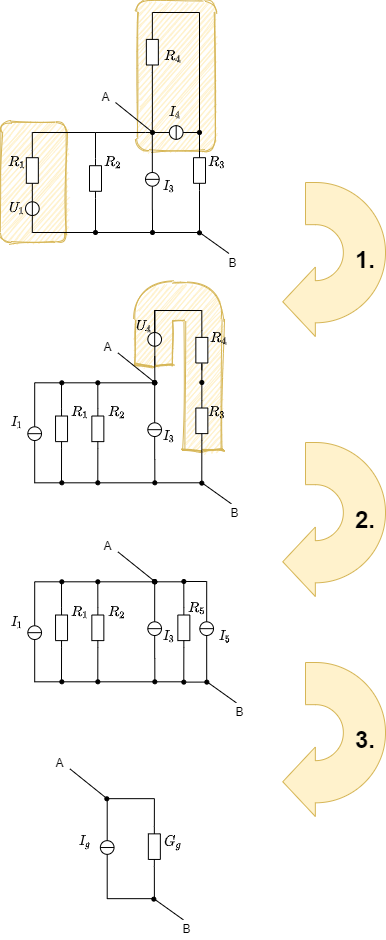
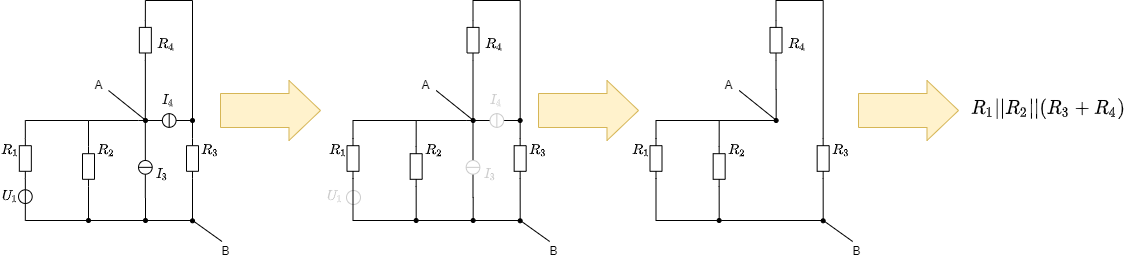
Diese Erkenntnis kann nun aber auch bei komplizierteren Schaltungen genutzt werden. In Abbildung 8 ist eine solche Schaltung gezeichnet. Diese soll in einen gesuchten Ersatzleitwert $G_g$ und eine gesuchte Ersatzstromquelle mit $I_g$ umgewandelt werden.
Wichtig hierbei: Es können nur Zweipole über die Quellen-Dualität umgewandelt werden. D.h. es dürfen bei ausgewählten Teilbereichen der Schaltung nur 2 Knoten als Ausgangsklemmen agieren. Gibt es mehr Knoten ist die Umwandlung nicht möglich.
- Als erstem Schritt sollen Quellen so umgewandelt werden, dass nach der Umwandlung Widerständer zusammengefasst werden können. In diesem Beispiel geschieht dies durch:
- die Umwandlung der linearen Spannungsquelle $R_1$ und $U_1$ in eine lineare Stromquelle mit $I_1={{U_1}\over{R_1}}$ und $R_1$ (bzw. $G_1={{1}\over{R_1}}$)
- die Umwandlung der linearen Stromquelle $R_4$ und $I_4$ in eine lineare Spannungsquelle mit $U_4={{I_4}\cdot{R_4}}$ und $R_4$
- Im zweiten Schritt kann die in 1. gebildete lineare Spannungsquelle $U_4$ mit $R_4$ mit dem Widerstand $R_3$ verbunden werden. Daraus kann wieder eine lineare Stromquelle erstellt werden. Diese hat nun einen Widerstand von $R_5 = R_3+R_4$ und eine ideale Stromquelle mit $I_5 = {{U_4}\over{R_3+R_4}}= {{{I_4}\cdot{R_4}}\over{R_3+R_4}} $.
- Das nun entstandene Schaltbild ist eine Parallelschaltung von idealen Stromquellen und Widerständen. Damit lassen sich die Werte der idealen Ersatzstromquelle und des Ersatzwiderstands ermitteln:
- ideale Ersatzstromquelle $I_g$: \begin{align*} I_g = I_1 + I_3 + I_5 = I_1 + I_3 + I_4\cdot{{R_4}\over{R_3+R_4}} \end{align*}
- Ersatzleitwert $G_g$: \begin{align*} G_g = \Sigma G_i = {{1}\over{R_1}}+{{1}\over{R_2}}+{{1}\over{R_5}}={{1}\over{R_1}}+{{1}\over{R_2}}+{{1}\over{R_3+R_4}} \end{align*}
vereinfachte Ermittlung des Innenwiderstands
Merke:
Ist nur der Ersatzwiderstand einer komplexeren Schaltung gesucht, so kann folgender Ansatz genutzt werden:
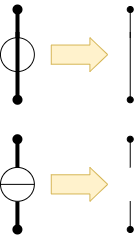
- Ersetze alle ideale Spannungsquellen durch einen Kurzschluss
(= Innenwiderstand der idealen Spannungsquelle) - Ersetze alle ideale Stromquellen durch eine offenen Kontakt
(= Innenwiderstand der idealen Stromquelle) - Füge die übriggebliebenen Widerstände über die Regeln zu Parallel- und Reihenschaltung zu einem Ersatzwiderstand zusammen.
Die Ersatzschaltungen für die idealen Quellen sind über die Schaltbilder ersichtlich (siehe Abbildung 13).
Damit kann auch der Ersatzwiderstand der obigen komplexen Schaltung schnell hergeleitet werden.
Für den Quellstrom $I_0$ ideale Ersatzstromquelle bzw. der Quellspannung $U_0$ ideale Ersatzspannungsquelle kann diese Herleitung nicht genutzt werden.
Aufgabe 3.2.1 Lösung einer Schaltungsvereinfachung I
Aufgabe 3.2.2 Lösung einer Schaltungsvereinfachung II
Aufgabe 3.2.3 Lösungsskizze für eine schwierigere Schaltungsvereinfachung
Aufgabe 3.2.4 3 kurze, aber interessante Schaltungsaufgaben
3.3 Leistung an Zweipolen und Bezugsgrößen
Ziele
Nach dieser Lektion sollten Sie:
- die Quellenleistung und Verbraucherleistung berechnen können.
- die Optimierungsziele für Energietechnik und Nachrichtentechnik unterscheiden können.
- den Wirkungsgrad und Ausnutzungsgrad berechnen können.
Leistung und Wirkungsgrad wurden bereits im 1. Kapitel und 2. Kapitel für einen einfachen Gleichstrom-Stromkreis betrachtet. Im Folgenden soll dies nochmals mit den Kenntnissen der Zweipole analysiert werden. Gerade für die Bereiche der Nachrichten- und Energietechnik ist dies wichtig. Die Ziele sind dabei unterschiedlich:
- In Energietechnik ist die Leistungsübertragung das Ziel. Die Leistung soll damit möglichst ohne Verluste abgegeben werden.
- In Nachrichtentechnik ist die Informationsübertragung im Fokus. Damit z.B. aus einer Antenne das bestmögliche Signal entnommen werden kann, muss hier die maximale Leistung entnommen werden.
Diese beiden Ziele scheinen zunächst das ähnlich zu klingen, sind aber deutlich zu unterscheiden, wie gleich zu sehen sein wird.
Leistungsmessung
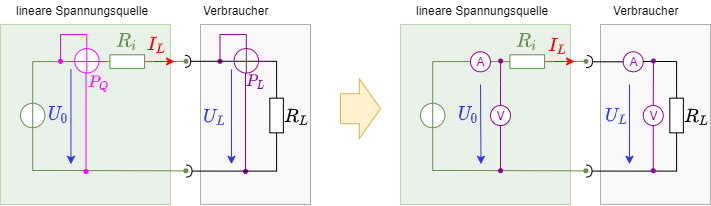
Zunächst muss betrachtet werden, wie die Leistung bestimmt werden kann. Das Leistungsmessgerät (oder Wattmeter) besteht aus einem kombinierten Amperemeter und Voltmeter.
In Abbildung 15 ist das Wattmeter mit dem Schaltsymbol als rundes Element mit gekreuzten Messeingängen zu sehen. In der Schaltung ist auch je eine Wattmeter für die (nicht außen messbare) abgegebene Leistung der idealen Quelle $P_Q$ und die aufgenommene Leistung des Verbrauchers $P_R$ eingezeichnet.
Die Simulation in Abbildung 16 zeigt folgendes:
- Die Schaltung mit linearer Spannungsquelle ($U_0$ und $R_i$), sowie einer ohmschen Last $R_L$.
- Einem nachgebildeten Wattmeter, wobei das Amperemeter durch ein Messwiderstand $R_S$ (englisch: Shunt) und eine Spannungsmessung für $U_S$ umgesetzt ist. Die Leistung ist dann: $P_L = {{1}\over{R_S}}\cdot U_S \cdot U_L$.
- im Oszilloskop-Bereich (unten)
- Links ist ist die Leistung
P_Lüber die Zeit in einem Diagramm aufgetragen. - Rechts ist das bereits bekannte Strom-Spannungs-Diagramm der aktuellen Werte dargestellt.
- Den Schieberegler
Lastwiderstand R_L, mit welchem der Wert des Lastwiderstands $R_L$ geändert werden kann.
Versuchen Sie nun in der Simulation den Wert des Lastwiderstands $R_L$ (Schieberegler) so zu variieren, dass sich die maximale Leistung einstellt. Welcher Widerstandswert stellt sich ein?
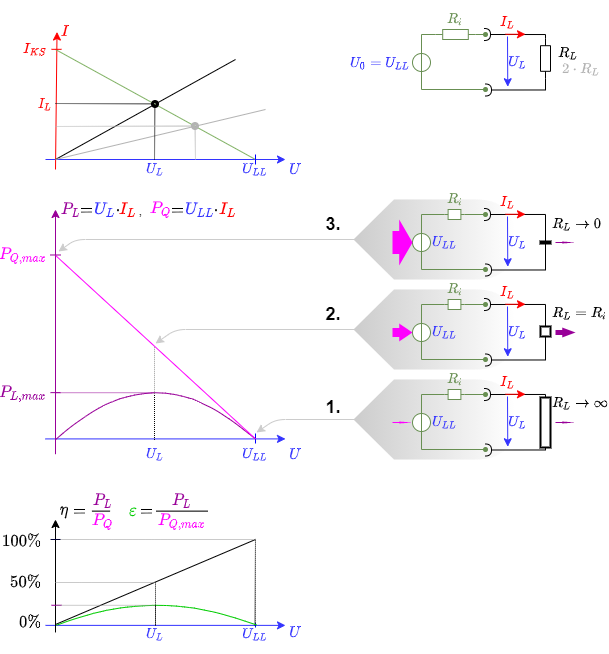
Abbildung 17 zeigt drei Diagramme:
- Diagramm oben: Strom-Spannungs-Diagramm der linearen Spannungsquelle.
- Diagramm mittig: Quellenleistung $P_Q$ und Verbraucherleistung $P_L$ über abgegebene Spannung $U_L$
- Diagramm unten: Wirkungsgrad über abgegebene Spannung $U_L$
Die beiden Leistungen sind wie folgt definiert:
- Quellenleistung: $\, \, \large{ P_Q = U_0 \cdot I_L} $
- Verbraucherleistung: $\large{ P_L = U_L \cdot I_L} $
- Beide Leistungen $P_Q$ und $P_L$ sind ohne Stromfluss gleich 0. Die Quellenleistung wird maximal, bei maximalem Stromfluss, also wenn der Verbraucherwiderstand $R_L=0$. In diesem Fall fließt die gesamte Leistung über den internen Widerstand ab. Der Wirkungsgrad fällt auf $0\%$. Dies ist beispielsweise bei einer durch einen Draht kurzgeschlossenen Batterie der Fall.
- Wird der Verbraucherwiderstand gerade so groß wie der Innenwiderstand $R_L=R_i$, so ergibt sich ein Spannungsteiler bei dem die Verbraucherspannung gerade die halbe Leerlaufspannung wird: $U_L = {{1}\over{2}}\cdot U_{LL}$. Andererseits ist auch der Strom halb so groß, wie der Kurzschlussstrom $I_L=I_{KS}$, da der Widerstand an der idealen Spannungsquelle doppelt so groß als im Kurzschlussfall.
- Wird der Verbraucherwiderstand hochohmig $R_L\rightarrow\infty$, so fließt zwar immer weniger Strom, aber immer mehr Spannung fällt am Verbraucher ab. Damit steigt der Wirkungsgrad und nähert sich $100\%$ für $R_L\rightarrow\infty$.
Der ganze Zusammenhang kann in einer ausführlichen Simulation nochmals analysiert werden.
In der Energietechnik ist eine Situation nahe an (1.) gewünscht: Maximale Leistungsabgabe bei geringsten Verlusten am Innenwiderstand der Quelle. Der Innenwiderstand der Quelle sollte also im Vergleich zum Verbraucher niedrig sein $R_L \gg R_i $. Der Wirkungsgrad soll gegen $100\%$ gehen und lässt sich folgendermaßen berechnen:
\begin{align*}\eta = {{P_{ab}}\over{P_{zu}}} = {{R_L\cdot I_L^2}\over{(R_L+R_i) \cdot I_L^2}} \\ \boxed{ \eta = {{R_L}\over{R_L+R_i}} } \end{align*}
In der Nachrichtentechnik ist eine Situation eine andere und entspricht der Situation (2.): Es soll die maximale Leistung aus der Quelle entnommen werden, ohne Rücksicht auf die Verluste über den Innenwiderstand. Dazu wird der Innenwiderstand der Quelle (z.B. eines Empfängers) und des Verbrauchers (z.B. der nachgelagerten Auswertung) aufeinander abgestimmt. Dieser Fall wird Leistungsanpassung oder Widerstandsanpassung genannt.
Video
Erklärung der Leistungsanpassung