Musterlösung Wintersemester 2020/2021
Aufgabe 5.4.2 Feldstärke in unterschiedlicher Geometrie I (Klausuraufgabe, ca 6% einer 60minütigen Klausur)
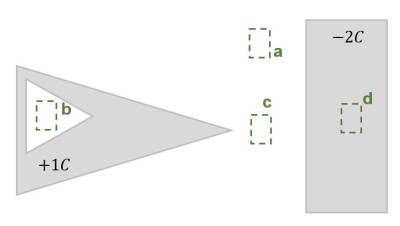
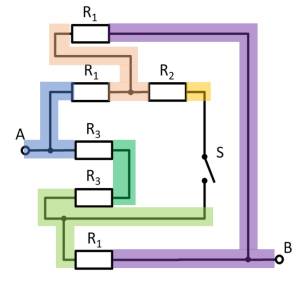
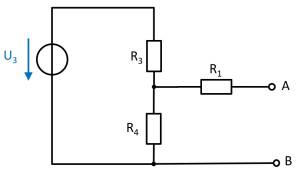
In der Abbildung rechts ist eine Anordnung aus idealen metallischen Leitern (grau) mit angegebener Ladung gezeigt. In weiß ist ein Dielektrikum (z.B. Vakuum) dargestellt. Mehrere, bezeichnete Bereiche sind durch grün gestrichelte Rahmen eingezeichnet, welche sich teilweise im Innern der Objekte befinden.
Ordnen Sie die bezeichneten Bereiche eindeutig nach aufsteigender Feldstärke (Betrag)! Geben Sie auch an, wenn bezeichneten Bereiche betragsmäßig die gleiche Feldstärke haben.
- Welches Feld herrscht in einem Raum vor, der vollständig durch einen leitfähigen Leiter umgeben wird?
- Wie verhält sich das Feld im Inneren eines Leiters?
- Erhöht oder sinkt die Feldstärke, wenn sich eine Ladung sich von einer anderen Ladung wegbewegt?
- Ist das Feld an bei einer Spitze höher oder niedriger?
- Bei $b$ und $d$ ist kein Feld messbar, da der umgebene Leiter auf einem konstanten Feld liegt. Er ergibt sich keine Potentialdifferenz und damit auch kein Feld.
- Bei $c$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt. Durch die Spitze kommt es zu einer Ladungsüberhöhung und damit zu einem höheren Feld.
- Bei $a$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt.
Aufgabe 5.1.3 Kräfte auf Ladungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
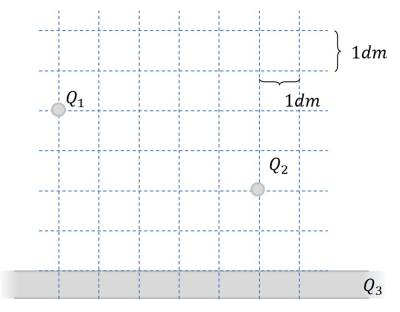
Gegeben ist eine im Vakuum befindliche Anordnung elektrischer Ladungen (siehe Bild rechts).
Die Ladungen haben folgende Werte:
$Q_1=7 μC$ (Punktladung)
$Q_2=5 μC$ (Punktladung)
$Q_3=0 C$ (unendlich ausgedehnte Flächenladung)
$\varepsilon_0=8,854\cdot 10^{-12} F/m$ , $\varepsilon_r=1$
1. Berechnen Sie Betrag der Kraft von $Q_2$ auf $Q_1$, ohne die Kraftwirkung von $Q_3$.
- Welche Gleichung ist für die Kraftwirkung von Ladungen anzuwenden?
- Wie lässt sich der Abstand zwischen den beiden Ladungen ermitteln?
2. Ist diese Kraft anziehend oder abstoßend?
- Welche Kraftwirkung zeigen gleich bzw. gegensätzlich geladene Körper aufeinander?
3. Nun sei $Q_2=0$ und die Flächenladung $Q_3$ in der Art gestaltet, dass sich ein homogenes elektrisches Feld mit $E_3=100 kV/m$ ergibt.
Welche Kraft (Betrag) ergibt sich nun auf $Q_1$?
- Welche Gleichung ist für die Kraftwirkung im homogenen Feld anzuwenden?
Aufgabe 5.2.1 mehrere Kräfte auf eine Ladung I (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
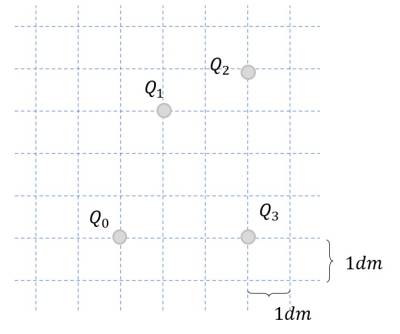
Gegeben ist die die Anordnung elektrischer Ladungen im Bild rechts.
Es ergeben sich folgende Kraftwirkungen:
$F_{01}=-5 N$
$F_{02}=-6 N$
$F_{03}=+3 N$
Ermitteln Sie rechnerisch die den Betrag der resultierenden Kraft.
- Wie müssen die Kräfte vorbereitet werden, dass sie tatsächlich addiert werden können?
Die vorhandenen Kräfte müssen in Koordinaten zerlegt werden. Hier empfehlen sich die orthogonalen Koordinaten ($x$ und $y$).
Das Koordinatensystem sei so ausgelegt, dass der Ursprung in $Q_0$ liegt mit der x-Achse in Richtung Q_3 und die y-Achse entsprechend rechtwinklig dazu.
Zur Koordinatenzerlegung sind die Winkel $alpha_{0n}$ der Kräfte zur x-Achse notwendig.
Diese ergeben sich im gewählten Koordinatensystem aus den Koordinaten der Ladungen: $\alpha_{0n} = atan(\frac{\Delta y}{\Delta x})$
$\alpha_{01} = atan(\frac{3}{1})= 1,249 = 71,6°$
$\alpha_{02} = atan(\frac{4}{3})= 0,927 = 53,1°$
$\alpha_{03} = atan(\frac{0}{3})= 0= 0°$
Dann ergeben sich die zerlegten Kräfte zu:
\begin{align*} F_{x,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{x,0n} = F_{0n} \cdot sin(\alpha_{0n}) \\ F_{x,0} &= (-5N) \cdot sin(71,6°) + (-6N) \cdot sin(53,1°) + (+3N) \cdot sin(0°) \\ F_{x,0} &= -2,18 N \\ \\ F_{y,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{y,0n} = F_{0n} \cdot cos(\alpha_{0n}) \\ F_{y,0} &= (-5N) \cdot cos(71,6°) + (-6N) \cdot cos(53,1°) + (+3N) \cdot cos(0°) \\ F_{y,0} &= -9,54 N \\ \\ \end{align*}
Aufgabe 2.7.7 Vereinfachen von Schaltungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
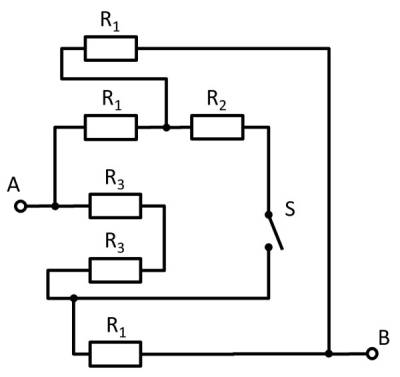
Gegeben ist die nebenstehende Schaltung mit
$R_1=10 \Omega$
$R_2=20 \Omega$
$R_3=5 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Der Schalter sollt dabei durch eine offene Leitung ersetzt werden.
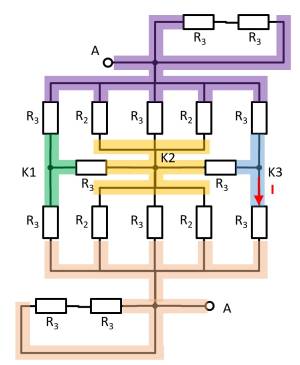
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
Es ergibt sich somit:
Damit lassen sich $R_3$ und $R_3$ zu $R_{33} = 2 \cdot R_3 = R_1$ zusammenfassen und es ergibt sich so ein linker und ein rechter Spannungsteiler.
Nun ist sichtbar, dass sich im linken und rechten Spannungsteiler das gleiche Potential am jeweiligen Abzweig, bzw. am Knoten K1 (grün) und K2 (pink).
Der Gesamtwiderstand lässt sich also berechnen als $R_{ges} = (2 \cdot R_1)||(2 \cdot R_1)$.
Durch die Symmetrie können aber auch die Knoten K1 und K2 kurzgeschlossen werden. Es gilt also auch $R_{ges} = 2 \cdot \left( R_1||R_1 \right)$.
2. Welcher Gesamtwiderstand ergibt sich, wenn Schalter $S$ geschlossen wird?
Der Widerstand bleibt also gleich.
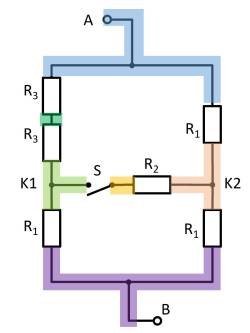
Aufgabe 2.7.8: Vereinfachen von Schaltungen II (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$R_2=10 \Omega$
$R_3=20 \Omega$
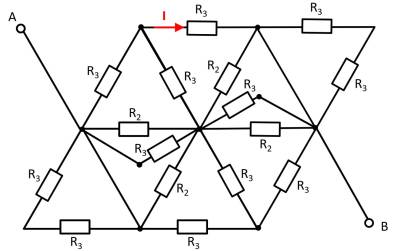
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Schalter (falls vorhanden) sollten dabei durch eine offene oder kurzgeschlossene Leitung ersetzt werden.
- Ergeben sich gleiche Potentiale an verschiedenen Knoten, die geschickt genutzt werden können?
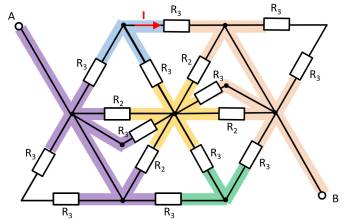
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
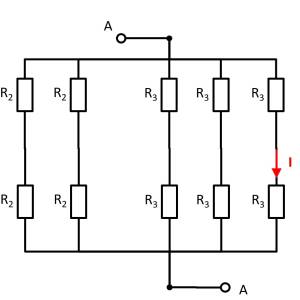
Es zeigt sich, dass die beiden Widerstände $R_3$ oben links und unten rechts jeweils kurzgeschlossen sind. Es ergibt sich somit:
Hier hilft es das Potential der Knoten K1, K2 und K3 zu betrachten. Bei K2 müssen dazu die Widerstände $R_2 || R_3 || R_2$ oben und unten jeweils zusammengefasst werden. Es ergeben sich also die gleichen Widerstandswerte oben und unten. Auch bei den Knoten K1 und K2 ergeben sich jeweils die gleichen Widerstandwerte oben wie unten. Mit den jeweils gleichen Verhältnissen der Widerstände bei K1, K2 und K3 lässt sich folgern, dass über die Widerstände $R_3$ zwischen K1 und K2 bzw. K2 und K3 kein Strom fließt. Diese tragen also nicht zum Gesamtwiderstand bei. In einem solchen Fall kann zwischen den relevanten Knoten für die Rechnung ein Kurzschluss oder eine offene Leitung frei gewählt werden. Im folgenden wird eine offene Leitung gewählt. Zusätzlich können die parallelen Stränge noch umsortiert werden.
Damit ergibt sich:
\begin{align*} R_{ges} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) \quad && || \quad \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{ges} &= R_2 \quad && || \quad \frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{ges} &= R_2 \quad && || \quad \frac{2}{3}\cdot R_3 \\ R_{ges} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} = \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Nun sei die Spannung von A nach B: $U_{AB}=U_0= 20 V$. Wie groß ist der Strom $I$?
Aufgabe 4.5.2: Leerlaufspannung über Superposition (Klausuraufgabe, ca 12% einer 60minütigen Klausur, WS2020)
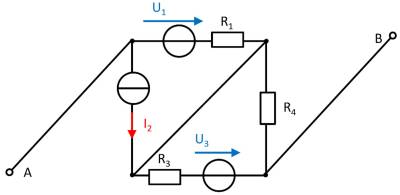
Gegeben ist die nebenstehende Schaltung mit
$R_1=5 \Omega$
$U_1=2 V$
$I_2=1 A$
$R_3=20 \Omega$
$U_3=8 V$
$R_4=10 \Omega$
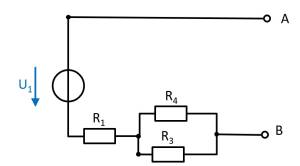
Bestimmen Sie die Leerlaufspannung zwischen A und B mittels des Superpositionsprinzips.
- Wie sehen die Einzelschaltungen aus, durch denen die Wirkungen (Spannung zwischen A und B) der einzelnen Quellen berechenbar wird?
Durch welchen Ersatzwiderstand muss eine Strom- bzw. eine Spannungsquelle bei der Berechnung der einzelnen Wirkungen ersetzt werden? - Wo liegen bei der Einzelbetrachtung die Leerlaufspannungen an?
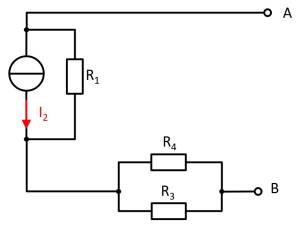
(Spannungs)Quelle $U_1$
- Stromquelle $I_2$ durch Kurzschluss ersetzen
- Spannungsquelle $U_3$ durch offene Leitung ersetzen
Werden die Komponenten verschoben, so ist die Schaltung besser zu verstehen:
Es zeigt sich, dass sich im Leerlauffall durch keinen Widerstand Strom fließt. Für die Wirkung gilt also: $U_{AB,1} = U_1$
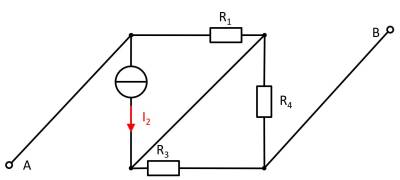
(Strom)Quelle $I_2$
- Spannungsquelle $U_1$ durch offene Leitung ersetzen
- Spannungsquelle $U_3$ durch offene Leitung ersetzen
Auch hier können Komponenten verschoben werden, um die Schaltung besser zu verstehen:
Hier erzeugt die Stromquelle $I_2$ am Widerstand $R_2$ die Spannung $U_{AB_2}$: $U_{AB,2} = - R_1 \cdot I_2$
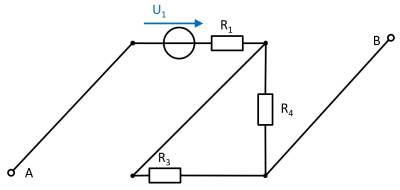
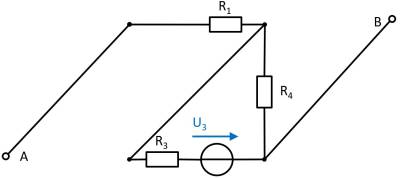
(Spannungs)Quelle $U_3$
- Spannungsquelle $U_1$ durch offene Leitung ersetzen
- Stromquelle $I_2$ durch Kurzschluss ersetzen
Ebenso wird auch hier die Schaltung verständlicher durch ein Verschieben der Komponenten:
In dieser Schaltung ergibt sich im Leerlauffall ein unbelasteter Spannungsteiler über $R_3$ und $R_4$. Über den Widerstand $R_1$ fließt im Leerlauf kein Strom.
Es ergibt sich:
\begin{align*} U_{AB,3} = \frac{R_4}{R_3 + R_4} \cdot U_3 \end{align*}
Resultierende Spannung
\begin{align*} U_{AB} &= U_1 - R_1 \cdot I_2 + \frac{R_4}{R_3 + R_4} \cdot U_3 \\ \end{align*}
Aufgabe 3.1.3: Last an linearer Quelle (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
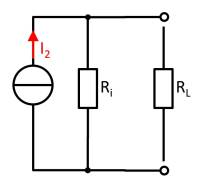
Gegeben ist eine lineare Stromquelle, welche eine ohmsche Last $R_L=10\Omega$ versorgt. Es ergibt sich ein Strom an der Last von $I_L=2A$. Der Kurzschlussstrom ist $5 A$.
1. Zeichnen Sie das Ersatzschaltbild des Aufbaus.
- Wie Sieht eine lineare Stromquelle aus?
- Wie wird die Last verschalten?
2. Wie groß die der Innenleitwert der Quelle?
- Im Kurzschlussfall fließt der Kurzschlussstrom nur durch $R_L$
- Für eine Vereinfachung der Rechnung bietet es sich an die lineare Stromquelle in eine lineare Spannungsquelle umzuwandeln.
Die Umwandlung wandelt auch die Schaltung von einer Parallelschaltung in eine Reihenschaltung.
Die Spannung $U_{LL}$ liegt also am Spannungsteiler aus $R_i$ und $R_L$: $U_{LL} = U_i + U_L$
Mit dem Lastwiderstand $R_L$ ergibt sich ein Strom von $I_L$ durch die Reihenschaltung.
Mit den gegebenen $R_L$ und $I_L$ lässt sich die Spannung $U_L$ an der Last berechnen.
Die restliche Spannung $U_i$ liegt am Innenwiderstand $R_i$ an, durch den auch der Strom $I_L$ fließt. Somit ergibt sich für den Leitwert $G_i$:
\begin{align*} U_{LL} &= U_i + U_L \\ R_i \cdot I_{KS} &= R_i \cdot I_L + R_L \cdot I_L \\ R_i \cdot I_{KS} - R_i \cdot I_L &= R_L \cdot I_L \\ R_i \cdot (I_{KS} - I_L) &= R_L \cdot I_L \\ R_i &= R_L \cdot \frac{I_L}{I_{KS} - I_L} \\ G_i &= \frac{I_{KS} - I_L}{R_L \cdot I_L} \\ \end{align*}
3. Welche Leistung nimmt die Last auf?
Aufgabe 1.7.6: temperaturabhängiger Widerstand einer Wicklung (Klausuraufgabe, ca 6% einer 60minütigen Klausur, WS2020)
Auf dem Rotor eines Asynchronmotors sind die Wicklungen in Kupfer ausgelegt. Die Länge des Wickeldrahts ist 40 m. Der Durchmesser ist 0,4 mm.
Beim Start des Motors ist dieser gleichmäßig auf die Umgebungstemperatur von 20°C abgekühlt.
Im Betrieb haben die Wicklungen auf dem Rotor eine Temperatur von 90°C.
$\alpha_{Cu,20°C}=0,0039 \frac{1}{K}$
$\beta_{Cu,20°C}=0,6 \cdot 10^{-6} \frac{1}{K^2}$
$\rho_{Cu,20°C}=0,0178 \frac{\Omega mm^2}{m}$
Verwenden Sie sowohl den linearen als auch quadratischen Temperaturkoeffizienten! 1. Bestimmen Sie den Widerstand der Leitung für $T = 20°C$.
2. Welche Widerstandserhöhung $\Delta R$ ist zwischen $20°C$ und $90°C$ bei einer Wicklung festzustellen?
Aufgabe 5.9.3: geschichteter Plattenkondensator (Klausuraufgabe, ca 6% einer 60minütigen Klausur, WS2020)
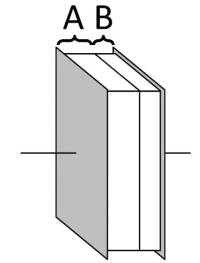
Bestimmen Sie die Kapazität $C$ für den rechts gezeichneten Plattenkondensator mit den folgenden Daten:
- rechteckige Elektroden mit einer Kantenlänge von $6 cm$ und $8 cm$
- Abstand der Platten: $2 mm$
- Dielektrikum A:
- $\varepsilon_{r,A} = 1 (Luft)$
- Dicke $d_A = 1,5 mm$
- Dielektrikum B:
- $\varepsilon_{r,B} = 100 (Eis)$
- Dicke $d_B = 0,5 mm$
$\varepsilon_{0} = 8,854 \cdot 10^{-12} F/m$
- Durch welche Schaltung lässt sich ein geschichteter Aufbau mit unterschiedlichen Dielektrika ersetzen?
Es ergibt sich somit: $C = \frac{C_A \cdot C_B}{C_A + C_B}$
Die Teilkapazität $C_A$ lässt sich berechnen durch \begin{align*} C_A &= \varepsilon_{0} \varepsilon_{r,A} \cdot \frac{A}{d_A} && | \text{mit } A = 3 cm \cdot 5cm = 6 \cdot 10^{-2} \cdot 8 \cdot 10^{-2} m^2 = 48 \cdot 10^{-4} m^2\\ C_A &= 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{1,5 \cdot 10^{-3} m} \\ C_A &= 28,33 \cdot 10^{-12} F \\ \end{align*}
Die Teilkapazität $C_B$ lässt sich berechnen durch \begin{align*} C_B &= \varepsilon_{0} \varepsilon_{r,B} \cdot \frac{B}{d_B} \\ C_B &= 100 \cdot 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{0,5 \cdot 10^{-3} m} \\ C_B &= 8,500 \cdot 10^{-9} F \\ \end{align*}
Aufgabe 7.2.6: Laden und Entladen von RC-Gliedern (Klausuraufgabe, ca 11% einer 60minütigen Klausur, WS2020)
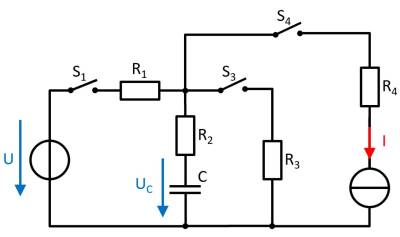
Gegeben ist die nebenstehende Schaltung mit
- $U = 10 V$
- $I = 4 mA$
- $R_1 = 100 \Omega, R_2 = 80 \Omega, R_3 = 50 \Omega, R_4 = 10 \Omega$
- $C = 40 nF$
Zu Beginn ist der Kondensator entladen, alle Schalter sind geöffnet. Der Schalter S1 wird zum Zeitpunkt t = 0 s geschlossen.
1. Bestimmen Sie die Zeitkonstante $\tau$ für diesen Ladevorgang.
- Welche Ersatzschaltung ergibt sich durch die Schalterstellung?
- Durch welche Größen lässt sich $\tau$ bestimmen?
- Wodurch fließt der Ladestrom?
2. Welche Spannung stellt sich am Kondensator $C$ zum Zeitpunkt $t=10 µs$ ein?
3. Wie hoch ist die Energie im Kondensator, wenn dieser vollständig geladen ist?
4. Bestimmen Sie die neue Zeitkonstante, die wirksam ist, wenn nach dem vollständigen Laden der Schalter S1 geöffnet und gleichzeitig S2 geschlossen wird.
5. Nachdem der Kondensator vollständig entladen wurde, werden alle Schalter wieder geöffnet.
Der Schalter S4 wird für $t = 1μs$ geschlossen.
Welche Spannung stellt sich an C ein?
- Durch die Stromquelle ergibt sich ein kontinuierlicher Fluss an Ladungen in den Kondensator.
- Die Widerstände auf dem Weg sind für den Strom in den Kondensator irrelevant. Sie erhöhen bei einer idealen Stromquelle nur die notwendige Spannung, um den Strom zu treiben.