Dies ist eine alte Version des Dokuments!
Musterlösung Wintersemester 2020/2021
Aufgabe 5.4.2 Feldstärke in unterschiedlicher Geometrie I (Klausuraufgabe, ca 6% einer 60minütigen Klausur)
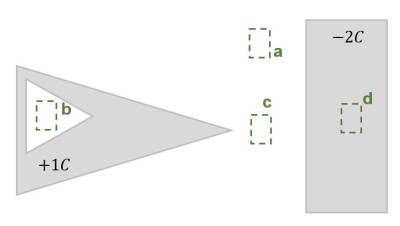
In der Abbildung rechts ist eine Anordnung aus idealen metallischen Leitern (grau) mit angegebener Ladung gezeigt. In weiß ist ein Dielektrikum (z.B. Vakuum) dargestellt. Mehrere, bezeichnete Bereiche sind durch grün gestrichelte Rahmen eingezeichnet, welche sich teilweise im Innern der Objekte befinden.
Ordnen Sie die bezeichneten Bereiche eindeutig nach aufsteigender Feldstärke (Betrag)! Geben Sie auch an, wenn bezeichneten Bereiche betragsmäßig die gleiche Feldstärke haben.
- Welches Feld herrscht in einem Raum vor, der vollständig durch einen leitfähigen Leiter umgeben wird?
- Wie verhält sich das Feld im Inneren eines Leiters?
- Erhöht oder sinkt die Feldstärke, wenn sich eine Ladung sich von einer anderen Ladung wegbewegt?
- Ist das Feld an bei einer Spitze höher oder niedriger?
- Bei $b$ und $d$ ist kein Feld messbar, da der umgebene Leiter auf einem konstanten Feld liegt. Er ergibt sich keine Potentialdifferenz und damit auch kein Feld.
- Bei $c$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt. Durch die Spitze kommt es zu einer Ladungsüberhöhung und damit zu einem höheren Feld.
- Bei $a$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt.
Aufgabe 5.1.3 Kräfte auf Ladungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
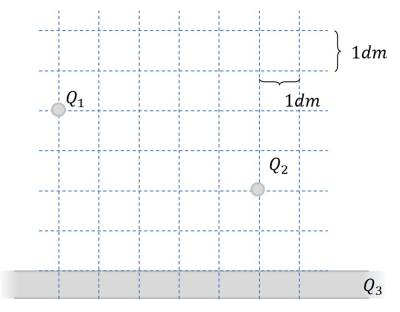
Gegeben ist eine im Vakuum befindliche Anordnung elektrischer Ladungen (siehe Bild rechts).
Die Ladungen haben folgende Werte:
$Q_1=7 μC$ (Punktladung)
$Q_2=5 μC$ (Punktladung)
$Q_3=0 C$ (unendlich ausgedehnte Flächenladung)
$\varepsilon_0=8,854\cdot 10^{-12} F/m$ , $\varepsilon_r=1$
1. Berechnen Sie Betrag der Kraft von $Q_2$ auf $Q_1$, ohne die Kraftwirkung von $Q_3$.
- Welche Gleichung ist für die Kraftwirkung von Ladungen anzuwenden?
- Wie lässt sich der Abstand zwischen den beiden Ladungen ermitteln?
2. Ist diese Kraft anziehend oder abstoßend?
- Welche Kraftwirkung zeigen gleich bzw. gegensätzlich geladene Körper aufeinander?
3. Nun sei $Q_2=0$ und die Flächenladung $Q_3$ in der Art gestaltet, dass sich ein homogenes elektrisches Feld mit $E_3=100 kV/m$ ergibt.
Welche Kraft (Betrag) ergibt sich nun auf $Q_1$?
- Welche Gleichung ist für die Kraftwirkung im homogenen Feld anzuwenden?
Aufgabe 5.2.1 mehrere Kräfte auf eine Ladung I (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
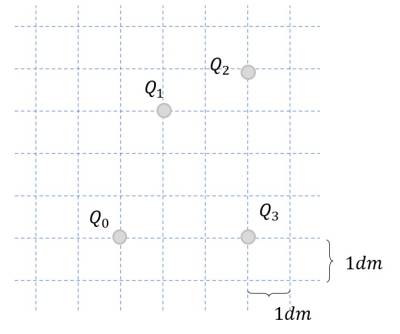
Gegeben ist die die Anordnung elektrischer Ladungen im Bild rechts.
Es ergeben sich folgende Kraftwirkungen:
$F_{01}=-5 N$
$F_{02}=-6 N$
$F_{03}=+3 N$
Ermitteln Sie rechnerisch die den Betrag der resultierenden Kraft.
- Wie müssen die Kräfte vorbereitet werden, dass sie tatsächlich addiert werden können?
Die vorhandenen Kräfte müssen in Koordinaten zerlegt werden. Hier empfehlen sich die orthogonalen Koordinaten ($x$ und $y$).
Das Koordinatensystem sei so ausgelegt, dass der Ursprung in $Q_0$ liegt mit der x-Achse in Richtung Q_3 und die y-Achse entsprechend rechtwinklig dazu.
Zur Koordinatenzerlegung sind die Winkel $alpha_{0n}$ der Kräfte zur x-Achse notwendig.
Diese ergeben sich im gewählten Koordinatensystem aus den Koordinaten der Ladungen: $\alpha_{0n} = atan(\frac{\Delta y}{\Delta x})$
$\alpha_{01} = atan(\frac{3}{1})= 1,249 = 71,6°$
$\alpha_{02} = atan(\frac{4}{3})= 0,927 = 53,1°$
$\alpha_{03} = atan(\frac{0}{3})= 0= 0°$
Dann ergeben sich die zerlegten Kräfte zu:
\begin{align*} F_{x,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{x,0n} = F_{0n} \cdot sin(\alpha_{0n}) \\ F_{x,0} &= (-5N) \cdot sin(71,6°) + (-6N) \cdot sin(53,1°) + (+3N) \cdot sin(0°) \\ F_{x,0} &= -2,18 N \\ \\ F_{y,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{y,0n} = F_{0n} \cdot cos(\alpha_{0n}) \\ F_{y,0} &= (-5N) \cdot cos(71,6°) + (-6N) \cdot cos(53,1°) + (+3N) \cdot cos(0°) \\ F_{y,0} &= -9,54 N \\ \\ \end{align*}
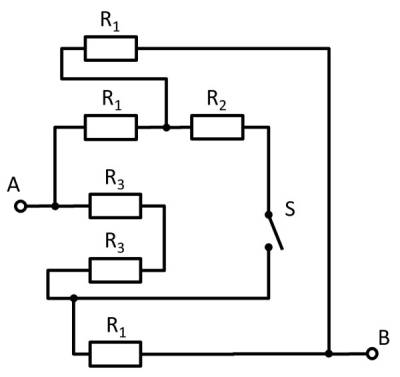
Aufgabe 2.7.7 Vereinfachen von Schaltungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
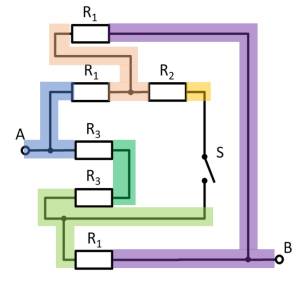
Gegeben ist die nebenstehende Schaltung mit
$R_1=10 \Omega$
$R_2=20 \Omega$
$R_3=5 \Omega$
und dem Schalter $S$.
1. Bestimmen Sie den Gesamtwiderstand $R_{ges}$ zwischen A und B durch Zusammenfassen der Widerstände bei offenem Schalter $S$.
- Wie lässt sich die Schaltung besser darstellen bzw. auseinanderziehen?
- Der Schalter sollt dabei durch eine offene Leitung ersetzt werden.
Hierzu können die einzelnen Zweige farbig hervorgehoben und als „leitfähiges Gummiband“ interpretiert werden.
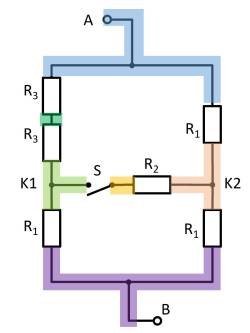
Es ergibt sich somit:
Damit lassen sich $R_3$ und $R_3$ zu $R_{33} = 2 \cdot R_3 = R_1$ zusammenfassen und es ergibt sich so ein linker und ein rechter Spannungsteiler.
Nun ist sichtbar, dass sich im linken und rechten Spannungsteiler das gleiche Potential am jeweiligen Abzweig, bzw. am Knoten K1 (grün) und K2 (pink).
Der Gesamtwiderstand lässt sich also berechnen als $R_{ges} = (2 \cdot R_1)||(2 \cdot R_1)$.
Durch die Symmetrie können aber auch die Knoten K1 und K2 kurzgeschlossen werden. Es gilt also auch $R_{ges} = 2 \cdot \left( R_1||R_1 \right)$.
2. Welcher Gesamtwiderstand ergibt sich, wenn Schalter $S$ geschlossen wird?
Der Widerstand bleibt also gleich.