This is an old revision of the document!
7. Schaltvorgänge an RC-Kombinationen
- Kondensator in IC's --> MOSFET
- Laden / Entladen von FET-Kondensator
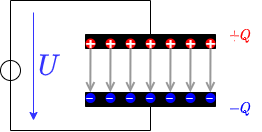
Im vorherigen Kapitel wurde bereits der Kondensator beschrieben. Er besteht aus zwei isolierten Leitern, die von einem Isolator getrennt sind (vgl. figure 1).
Sie dienen als Energiespeicher. Dies geschieht in folgender Art:
- Eine äußere Quelle zieht Ladungsträger von einer der Elektroden ab und befördert diese zur anderen Elektrode
- Ist die äußere Quelle eine Spannungsquelle mit der Spannung $U$ so stellt sich nach einer gewissen Zeit ein stationärer Zustand ein.
In diesem ist eine fester Anzahl $+Q$ auf der positiven Elektrode und $-Q$ auf der negativen Elektrode. - Diese Ladungen bilden in Zwischenraum der Elektroden ein elektrisches Feld aus. Dieses Feld speichert die zugeführte Energie.
Es gilt: Je größer die Spannung $U$ ist, desto mehr Ladungen $Q$ werden auf der Elektrode gespeichert. Dieser Zusammenhang ist direkt proportional mit der Proportionalitätskonstante $C$:
\begin{align*} C = {{Q}\over{U}} \quad \quad \text{mit:} \quad [C]=1 {{As}\over{V}}= 1 F = 1 Farad \end{align*}
Aber nicht immer ist direkt zu erkennen, das ein Aufbau einen Kondensator enthält.
So sind folgende Beispiele auch Kondensatoren:
- offener Schalter: Liegt zwischen den beiden Metallteilen eine Spannung an, so können sich dort auch Ladungen ansammeln.
Da die Abstände in der Regel groß sind und als Dielektrikum Luft verwendet wird, ist die Kapazität des so gebildeten Kondensators sehr klein. - Freileitung: Eine Freileitung stellt gegen das Massepotential des Erdbodens auch ein Kondensator dar. Das Laden und Entladen durch den Wechselstrom führt dazu, dass sich polarisierbare Moleküle Ausrichten können. So werden z.B. die Wassertropfen in der Nähe der Leitung durch das Feld durchgewalkt und brummen mit $100Hz$ und vielfachem davon (Oberwellen). Durch Spitzenentladung ergibt sich das hochfrequente Knistern.
- Leiterbahn: Auch eine Leiterbahn auf einer Platine kann gegen eine naheliegende Massefläche einen Kondensator darstellen. Dies kann für digitale Signale eine Problem darstellen (sieh Lade- und Entladekurven im Folgenden)
- Menschlicher Körper: Der menschliche Körper kann ebenso Ladung aufnehmen. Die so aufgenommene Ladung bildet gegenüber anderen Objekten einen Kondensator. Dieser kann auf einige $kV$ aufgeladen werden. Dies macht besondert in Elektrolaboren Probleme, da durch die bloße Berührung von Bauteilen diese zerstört werden können.
- Membran von Nervenzellen: Auch bei Nervenzellen ergeben sich durch die Lipiddoppelschicht (Membran der Nervenzelle) und den zwei zellulären Flüssigkeiten mit unterschiedlichen Elektrolyten (Ionen) ergeben einen Kondensator. Die Nervenzellen sind für eine schnellere Übertragung mit einer dicken Schicht (Myelinschicht) umgeben. Diese senkt die Kapazität und erhöht damit das nacheinander stattfindende Aufladen aufeinanderfolgender Teile der Nervenzelle. Bei Krankheiten wie Creutzfeldt–Jakob oder Multiple Sklerose dünnt sich diese Schicht aus. Dies führt zu verzögerter Signalübertragung welche die Krankheitsbilder prägt.
Im Folgenden soll der Ladevorgang eines Kondensators näher betrachtet werden. Dazu muss man sich vergegenwärtigen, dass beim Laden des Kondensators neben der Spannungsquelle $U_0$ und dem Kondensator $C$ immer auch ein Widerstand $R$ in der Schaltung vorliegt. Dieser setzt sich zusammen aus dem Innenwiderstand der (nicht-idealen) Spannungsquelle, dem Innenwiderstand des Kondensators und dem parasitären (=störenden) Widerstand der Leitung. Bei praktischen Anwendungen ist häufig erwünscht dass sich Kondensatoren in einem bestimmten Zeitbereich aufladen. Dazu wird ein weiterer, reeller Widerstand in die Schaltung eingefügt. Die so entstandene Aneinanderreihung von Widerstand und Kondensator wird RC-Glied genannt. Sie gleicht einem Spannungsteiler, bei dem ein Widerstand durch einen Kondensator ausgetauscht wurde.
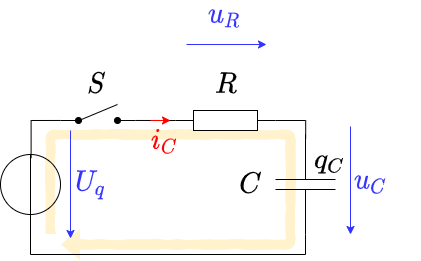
Um das Laden zu starten, wird noch ein (idealer) Schalter $S$ eingefügt.
Die zu betrachtende Schaltung sieht also dann aus wie in figure 2 gezeigt.
Ein idealer Schalter ist dabei gekennzeichnet durch:
- unendlich schnellem Schalten
- Widerstand von $0\Omega$ im geschlossenen Zustand (“Kurzschluss”)
- Widerstand $\rightarrow \infty$ im offenen Zustand (“offene Leitung”)
- keiner kapazitiven Wirkung
- Eine zeitlich veränderliche Spannung $u_C(t)$ am Kondensator oder die Spannung $u$ einer Wechselspannungsquelle im Gegensatz zu einer konstanten Spannung $U_0$ an einer Konstantspannungsquelle
- Ein zeitlich veränderlicher Strom $i_L(t)$ an einer Spule oder zeitlich veränderlicher Strom $i_L(t)$ an einem Kondensator
Da durch den kleinen Buchstaben bereits die Zeitabhängigkeit klar ist, wird bei diesen Größen gelegentlich diese nicht durch das nachgestellte $(t)$ angegeben. Es ist also $u = u(t)$.
7.1 Zeitverlauf des Lade- und Entladevorgangs
Ziele
Nach dieser Lektion sollten Sie:
- die Zeitkonstante $\tau$ kennen und insbesondere ausrechnen können.
- den Zeitverlauf der Ströme und Spannungen am RC-Glied bei gegebenem Widerstand und Kapazität ermitteln können.
- die Stetigkeitsbedingungen der elektrischen Größen kennen.
- wissen, ab wann (=nach welchem Maß) der Kondensator als vollständig aufgeladen / entladen gilt, also ein stationärer Zustand als erreicht betrachtet werden kann.
In der Simulation rechts sehen Sie die oben angesprochene Schaltung in einer etwas abgewandelten Form:
- Die Kapazität $C$ kann über den Widerstand $R$ geladen werden, wenn der Wechselschalter $S$ die Gleichspannungsquelle $U_0$ mit den beiden verbindet.
- Über den Schalter $S$ ist aber auch möglich die Reichenschaltung von $R$ und $C$ kurzzuschließen.
- Weiterhin wird der Strom $i_C$ und die Spannung $u_C$ im Oszilloskop als Datenpunkte über der Zeit und in der Schaltung als Zahlenwert angezeigt.
- Zusätzlich ist es möglich mit den Slidern
Capacitance CundResistance Rden Kapazitätswert $C$ und Widerstandswert $R$ zu verändern.
Aufgaben:
- Machen Sie sich damit vertraut, wie der Kondensatorstrom $i_C$ und die Kondensatorspannung $u_C$ von der vorgegebenen Kapazität $C$ und dem Widerstand $R$ abhängt.
Nutzen Sie dazu für $R=\{ 10\Omega, 100\Omega, 1k\Omega\}$ und $C=\{ 1\mu F, 10 \mu F\}$. Wie schnell steigt die Kondensatorspannung $u_C$ jeweils n? - Welche Größe ($i_C$ oder $u_C$) ist hier stetig? Warum muss diese stetig sein? Warum muss die andere Größe unstetig sein?
Diese Schaltung wird in Folgenden in zwei einzelne Schaltungen zerlegt, welche nur das Laden bzw. nur das Entladen betrachten.
Um den Ladevorgang eines Kondensators zu verstehen, soll ein zunächst ungeladener Kondensator mit der Kapazität $C$ über einen Widerstand $R$ von einer Gleichspannungsquelle $U_0$ geladen werden.
- Damit die Spannung $U_0$ zu einer bestimmten Zeit $t_0 = 0 s$ erst wirkt wird der Schalter $S$ zu diesem Zeitpunkt geschlossen.
- Direkt nach dem Zeitpunkt $t_0$ fließt der maximale Strom (“Ladestrom”) im Stromkreis. Dieser wird nur durch den Widerstand $R$ begrenzt. Der ungeladene Kondensator hat zu dem Zeitpunkt eine Spannung $u_C(t_0)=0V$. Die maximale Spannung $u_R(t_0)=U_0$ liegt am Widerstand an. Der Strom ist $i_C(t_0)={{U_0}\over{R}}$.
- Durch den Strom fließen Ladungsträger von einer Elektrode zur anderen. Damit wird der Kondensator geladen und seine Spannung steigt $u_C$.
- Somit reduziert sich die Spannung $u_R$ am Widerstand und damit auch der Strom $i_R$.
- Durch den so reduzierten Strom fließen weniger Ladungen auf der Kondensator.
- Idealerweise ist der Kondensator erst bei $t \rightarrow \infty$ vollständig auf die vorgegebene Spannung $U_0$ geladen. Er trägt dann die Ladung: $q(t \rightarrow \infty)=Q = C \cdot U_0$
Der Ablauf soll nun im Einzelnen in Formeln gefasst werden.
In der Schaltung werden lineare Bauteile genutzt, d.h. die Komponentenwerte für den Widerstand $R$ und die Kapazität $C$ sind unabhängig vom Strom oder der Spannung.
Dann gelten Definitionsgleichungen für den Widerstand $R$ und die Kapazität $C$ auch für zeitlich veränderliche oder infinitesimale Größen:
\begin{align*} R = {{u_R(t)}\over{i_R(t)}} = {{du_R}\over{di_R}} = const. \\ C = {{q(t)}\over{u_C(t)}} = {{dq}\over{du_C}} = const. \tag{7.1.1} \end{align*}
Die folgenden Erklärungen sind auch in diesen beiden Videos zum zum Laden und Entladen gut erklärt.
Laden eines Kondensators zum Zeitpunkt t=0
Durch die Betrachtung der Masche ergibt sich allgemein: Die Spannung der Quelle ist gleich der Summe der beiden Spannungen über Widerstand und Kondensator.
\begin{align*} U_0 =u_R + u_C = R \cdot i_C + u_C \tag{7.1.2} \end{align*}
Im ersten Augenblick $dt$ fließt durch den Strom $i_C$ ein infinitesimal kleines Ladungs“häppchen” $dq$ von der Spannungsquelle getrieben durch den Stromkreis.
Für diese ergibt sich mit $(7.1.1)$:
\begin{align*} i_C = {{dq}\over{dt}} \quad \quad \text{und} \quad dq = C \cdot du_C \end{align*}
Aus den beiden Formeln lässt sich der Ladestrom $i_C$ ermitteln:
\begin{align*} i_C = C \cdot {{du_C}\over{dt}} \tag{7.1.3} \end{align*}
Damit wird $(7.1.2)$ zu:
\begin{align*} U_0 &=u_R + u_C \\ &= R \cdot C \cdot {{du_C}\over{dt}} + u_C \end{align*}
- hier folgt etwas Mathematik:
-
Dieses Ergebnis stellt eine Differentialgleichung 1. Ordnung dar.
Dieses sollte generell so umgeschrieben werden, dass der (von der Variablen) abhängige Teil auf eine und der Rest auf der anderen Seite steht.
Dies liegt hier schon vor. Der passende Ansatz für ein solches Problem ist:\begin{align*} u_C(t) = \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \end{align*}
\begin{align*} U_0 &= R \cdot C \cdot {{d}\over{dt}}(\mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C}) + \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \\ &= R \cdot C \cdot \mathcal{AB} \cdot e^{\mathcal{B}\cdot t} + \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \\ U_0 - \mathcal{C} &= ( R \cdot C \cdot \mathcal{AB} + \mathcal{A} ) \cdot e^{\mathcal{B}\cdot t} \\ \end{align*}
Diese Gleichung muss für jedes $t$ gelten. Dies ist nur möglich wenn der linke als auch der rechte Term gleich 0 werden.
Es gilt also:\begin{align*} \mathcal{C} = U_0 \\ \\ R \cdot C \cdot \mathcal{AB} + \mathcal{A} &= 0 \quad \quad | : \mathcal{A} \quad | -1 \\ R \cdot C \cdot \mathcal{B} &= - 1 \\ \mathcal{B} &= - {{1}\over{R C}} \\ \end{align*}
Es ergibt sich also:
\begin{align*} u_C(t) = \mathcal{A} \cdot e^{\large{- {{t}\over{R C}} }} + U_0 \end{align*}
Für die Lösung muss noch gelten, dass zum Zeitpunkt $t_0=0$ gerade gilt $u_C(t_0) = 0$:
\begin{align*} 0 &= \mathcal{A} \cdot e^{\large{0}} + U_0 \\ 0 &= \mathcal{A} + U_0 \\ \mathcal{A} &= - U_0 \end{align*}
Die Lösung ist also:
\begin{align*} u_C(t) &= - U_0 \cdot e^{\large{- {{t}\over{R C}}}} + U_0 \end{align*}
Und damit ergibt sich: \begin{align*} u_C(t) &= U_0 \cdot (1 - e^{\large{- {{t}\over{R C}}}}) \end{align*}
Und mit $(7.1.3)$ wird $i_C$ zu: \begin{align*} i_C(t) &= {{U_0}\over{R}} \cdot e^{\large{- {{t}\over{R C}} } } \end{align*}
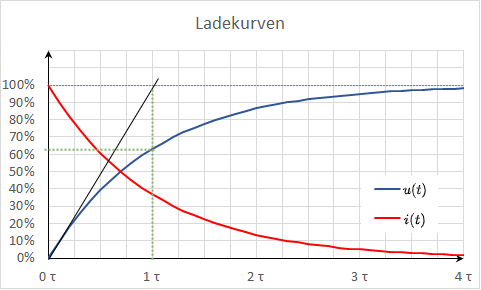
In figure 4 sind die beiden Zeitverläufe für die Ladespannung $u_C(t)$ und den Ladestrom $i_C(t)$ des Kondensators dargestellt.
Merke:
- Im Exponenten muss ein einheitenloser Term stehen. Also muss $RC$ auch eine Zeit darstellen.
Diese Zeit wird Zeitkonstante $\tau =R \cdot C$ genannt.
- Zum Zeitpunkt $t=\tau$ ergibt sich: $u_C(t) = U_0 \cdot (1 - e^{- 1}) = U_0 \cdot (1 - {{1}\over{e}}) = U_0 \cdot ({{e-1}\over{e}}) = 0,63 \cdot U_0 = 63\% \cdot U_0 $
Es wird also der Kondensator nach einem $\tau$ auf $63$% aufgeladen.
- Zum Zeitpunkt $t=2 \cdot \tau$ ergibt sich: $u_C(t) = U_0 \cdot (1 - e^{- 2}) = 86 \% \cdot U_0 = (63 \% + (1-63 \%) \cdot 63 \% ) \cdot U_0$
Nach jedem weiteren $\tau$ wird also der noch nicht aufgeladene Rest ($1-63 \%$) wieder zu $63\%$ aufgeladen.
- Nach etwa $t=5 \cdot \tau$ ergibt sich ein zu über $99\%$ geladener Kondensator.
In realen Schaltungen kann nach $5 \cdot \tau$ von einem geladenen Kondensator ausgegangen werden. - die Zeitkonstante $\tau$ kann auf mehrere Wege grafisch bestimmt werden:
- Eintragen des Spannungswertes welcher $63\%$ entspricht auf der y-Achse. Suchen des Schnittpunktes mit dem Graphen. Ablesen des Zeitpunkts (siehe grüne Linien in figure 4).
- Einzeichnen der Tangente zur (Spannungs)Ladekurve zum Zeitpunkt des entladenen Kondensators.
Diese schneidet eine horizontale Linie auf der Höhe der Ladespannung am Punkt $t=\tau$ (siehe schwarze und hellblaue Linien in figure 4).
Entladen eines Kondensators zum Zeitpunkt t=0
Für die Entladung wird folgende Situation betrachtet:
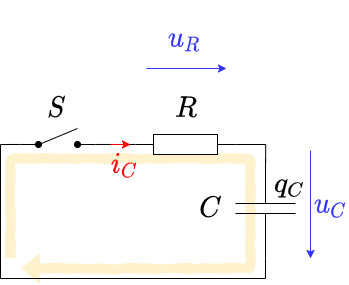
- Ein auf die Spannung $U_0$ geladener Kondensator mit der Kapazität $C$ wird über einen Widerstand $R$ zum Zeitpunkt $t=t_0$ kurzgeschlossen.
- Dadurch liegt anfangs die volle Spannung $U_0$ an dem Widerstand an: $u_R(t_0)=U_0$
- Der anfängliche Entladestrom wird damit über den Widerstand definiert: $i_C ={{u_R}\over{R}}$
- Durch die abfließenden Ladungen wird die Spannung des Kondensators $u_C$ abgesenkt, da gilt: $u_C = {{q(t)}{C}}$
- Idealerweise ist der Kondensator erst bei $t \rightarrow \infty$ vollständig entladen.
Auch dieser Ablauf soll nun im Einzelnen in Formel gefasst werden. Durch die Betrachtung der Masche ergibt sich allgemein: Die Summe der beiden Spannungen über Widerstand und Kondensator summieren sich auf Null.
\begin{align*} 0 =u_R + u_C = R \cdot i_C + u_C \end{align*}
Damit ergibt sich mit $(7.1.3)$:
\begin{align*} 0 =u_R + u_C = R \cdot C \cdot {{du_C}\over{dt}} + u_C \end{align*}
- auch hier nutzt etwas Mathematik:
-
Dieses Ergebnis stellt wieder eine Differentialgleichung 1. Ordnung dar.
Der passende Ansatz für ein solches Problem ist:\begin{align*} u_C(t) = \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \end{align*}
\begin{align*} 0 &= R \cdot C \cdot {{d}\over{dt}}(\mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C}) + \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \\ &= R \cdot C \cdot \mathcal{AB} \cdot e^{\mathcal{B}\cdot t} + \mathcal{A} \cdot e^{\mathcal{B}\cdot t} + \mathcal{C} \\ 0 - \mathcal{C} &= ( R \cdot C \cdot \mathcal{AB} + \mathcal{A} ) \cdot e^{\mathcal{B}\cdot t} \\ \end{align*}
Diese Gleichung muss für jedes $t$ gelten. Dies ist nur möglich wenn der linke als auch der rechte Term gleich 0 werden.
Es gilt also:\begin{align*} \mathcal{C} = 0 \\ \\ R \cdot C \cdot \mathcal{AB} + \mathcal{A} &= 0 \quad \quad | : \mathcal{A} \quad | -1 \\ R \cdot C \cdot \mathcal{B} &= - 1 \\ \mathcal{B} &= - {{1}\over{R C}} \\ \end{align*}
Es ergibt sich also:
\begin{align*} u_C(t) = \mathcal{A} \cdot e^{\large{- {{t}\over{R C}} }} \end{align*}
Für die Lösung muss noch gelten, dass zum Zeitpunkt $t_0=0$ gerade gilt $u_C(t_0) = U_0$:
\begin{align*} U_0 &= \mathcal{A} \cdot e^{\large{0}} \\ U_0 &= \mathcal{A} \\ \mathcal{A} &= U_0 \end{align*}
Und damit ergibt sich: \begin{align*} u_C(t) &= U_0 \cdot e^{\large{- {{t}\over{\tau}}}} \quad \text{mit} \quad \tau = R C \end{align*}
Und mit $(7.1.3)$ wird $i_C$ zu: \begin{align*} i_C(t) &= - {{U_0}\over{R}} \cdot e^{\large{- {{t}\over{R C}} } } \end{align*}
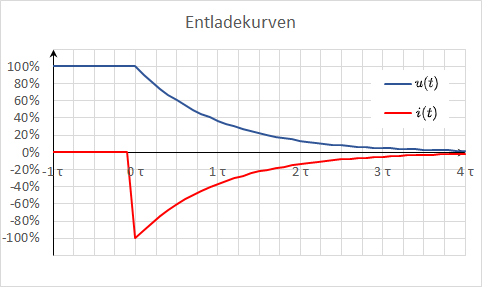
In figure 6 sind wieder die beiden Zeitverläufe dargestellt; diesmal für die Entladespannung $u_C(t)$ und den Entladestrom $i_C(t)$ des Kondensators.
Da Der Strom nun aus dem Kondensator herausfließt, ist das Vorzeichen von $i_C$ negativ.
Periodische Schaltvorgänge
In der Simulation rechts ist ein periodischer Schaltvorgang zu sehen. Dabei wird über den Schalter der Kondensator periodisch ge- und entladen.
Dabei sind in der Simulation drei Slider gegeben, um den Widerstand $R$ (Resistance R), die Kapazität $C$ (Capacity C) und die Frequenz $f$ (Frequency f) ändern zu können.
Im Verlauf unten in der Simulation ist die Spannung $u_C$ über den Kondensator in grün und der Strom $i_C$ in gelb dargestellt.
Aufgaben:
- Erhöhen Sie die die Frequenz auf $f=10kHz$ über den entsprechenden Slider. Welche Veränderung ergibt sich für $u_C$ und $i_C$?
- Erhöhen Sie nun zusätzlich die Kapazität auf $C=10 \mu F$ über den entsprechenden Slider. Welche Veränderung ergibt sich für $u_C$ und $i_C$?
- Erhöhen Sie nun zusätzlich den Widerstand auf $R= 1 k\Omega$ über den entsprechenden Slider. Welche Veränderung ergibt sich für $u_C$ und $i_C$?
7.2 Energie eines Kondensators
Ziele
Nach dieser Lektion sollten Sie:
- den Energieinhalt in einem Kondensator berechnen können.
- die Energieänderung eines Kondensators berechnen können, welche sich durch eine Änderung der Spannung zwischen den Kondensatoranschlüssen ergibt.
- (Anfangs)Strom, (End)Spannung und Ladung beim Ladungsausgleich von mehreren Kondensatoren (auch über Widerstände) berechnen können.
Es soll nun der Kondensator als Energiespeicher näher betrachtet werden. Laut des Kapitels ermittlung_der_elektrischen_leistung_im_gleichstrom-stromkreis ist die Leistung für konstante Werte (Gleichstom) definiert als:
\begin{align*} P={{\Delta W}\over{\Delta t}} = U \cdot I \end{align*}
Für veränderliche Signale ergibt sich die Momentanleistung als:
\begin{align*} p={{dw}\over{dt}} = u \cdot i \end{align*}
Beim Laden des Kondensators zum Zeitpunkt $t_0 = 0$ ergibt sich als für die gespeicherte Energie $W$ zu einem späteren Zeitpunkt $t_1 =t$:
\begin{align*} W = \int_{t0}^t1 dw = \int_{0}^t u \cdot i dt = \int_{0}^t u_C \cdot i_C dt \end{align*}
Beim Ladevorgang gilt
\begin{align*} u_C(t) = U_0 \cdot (1 - e^{ - {{t}\over{\tau}} }) \\ i_C(t) = {{U_0}\over{R}} \cdot e^{ -{{t}\over{\tau}} } \end{align*}
Insbesondere gilt:
\begin{align*} C = {{q(t)}\over{u_C(t)}} \quad &\rightarrow \quad &q(t) &= {u_C(t)}\cdot{C} \\ i_C(t) = {{d q(t)}\over{dt}} \quad &\xrightarrow{C=konst.} \quad &i_C(t) &= C \cdot {{d u_C(t)}\over{dt}} \end{align*}
Damit wird die gespeicherte Energie:
\begin{align*} W &= \int_{0}^t u_C(t) \cdot C \cdot {{d u_C(t)}\over{dt}} dt \\ &= C \cdot \int_{0}^{U} u_C(t) d u_C(t) \\ &= C \cdot \left[{{1}\over{2}} U^2 \right] _0^U \\ &= C \cdot U^2 \end{align*}
Herleitung der Energieinhalts eines Kondensators
Aufgaben
Aufgabe 7.2.1 Übungsaufgabe zum Laden/Entladen des Kondensators
Aufgabe 7.2.2 weitere Übungsaufgabe zum Laden/Entladen des Kondensators
Aufgabe 7.2.3 weitere Übungsaufgabe zum Laden des Kondensators
Aufgabe 7.2.4 Übungsaufgabe zum Ladungsausgleich zweier Kondensatoren