Dies ist eine alte Version des Dokuments!
2. Simple DC circuits
So far, only simple circuits consisting of a source and a load connected by wires have been considered.
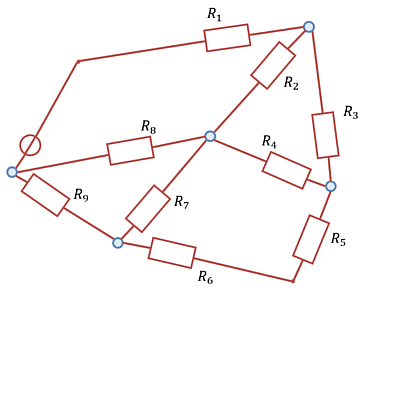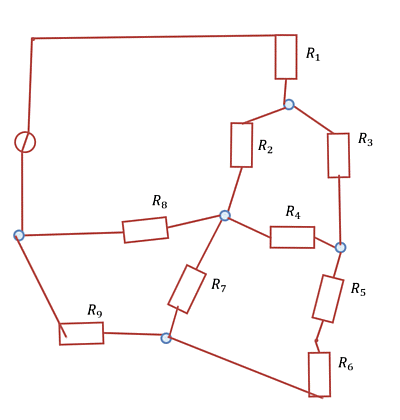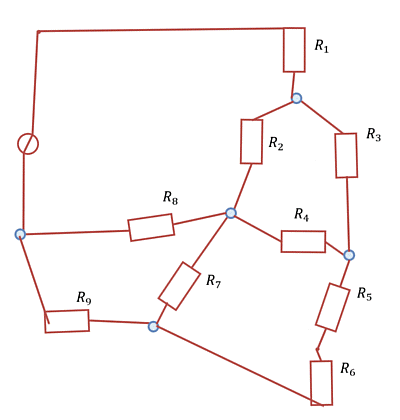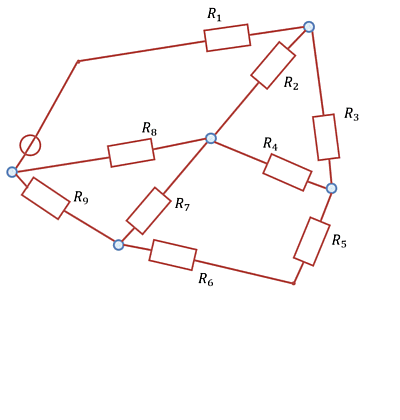
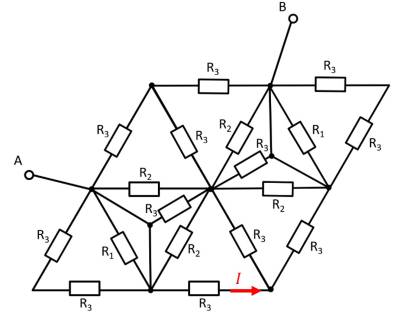
In the following, more complicated circuit arrangements will be analysed. These initially contain only one source, but several lines and many ohmic loads (cf. Abbildung 1).
2.1 ideal components
goals
After this lesson you should:
- Know the representation of ideal current and voltage sources in the U-I diagram.
- Know the internal resistance of ideal current and voltage sources.
- Know the symbol of ideal current and voltage sources.
- Know the properties of ideal resistance and ideal connection.
Every electrical circuit consists of three elements:
- Consumers: consumers convert electrical energy into energy that is not purely electrical.
e.g.- into electrostatic energy (capacitor)
- into magnetostatic energy (magnet)
- into electromagnetic energy (LED, light bulb)
- into mechanical energy (loudspeaker, motor)
- into chemical energy (charging an accumulator)
- sources (generators): sources convert energy from another form of energy into electrical energy. (e.g. generator, battery, photovoltaic).
- wires (interconnections): the wires of interconnection lines link consumers to sources.
These elements will be considered in more detail below.
Consumer
- The colloquial term 'consumer' in electrical engineering stands for an electrical consumer - i.e. a component which converts electrical energy into another form of energy.
- A resistor is often also referred to as a consumer. In addition to pure ohmic consumers, however, there are also ohmic-inductive consumers (e.g. coils in a motor) or ohmic-capacitive consumers (e.g. various power supplies using capacitors at the output). Correspondingly the equation „consumer is a resistor“ is wrong.
- Current-voltage characteristics (vgl. Abbildung 2)
- Current-voltage characteristics of a load always run through the origin, because without current there is no voltage and vice versa.
- Ohmic loads have a linear current-voltage characteristic which can be described by a single numerical value.
The slope in the $U$-$I$-characteristic is the conductance: $I = G \cdot U = {{U}\over{R}}$
Sources
- Sources act as generators of electrical energy
- A distinction is made between ideal and real sources.
The real sources are described in the following chapter (non-ideal_sources_and_two_terminal_networks).
The ideal voltage source generates a defined constant output voltage $U_s$ (in German often $U_q$ for Quellenspannung).
In order to maintain this voltage, it can supply any current.
The current-voltage characteristic also represents this (see Abbildung 3).
The circuit symbol shows a circle with two terminals. In the circuit, the two terminals are short-circuited.
Another circuit symbol shows the negative terminal of the voltage source as a „thick minus symbol“, the positive terminal is drawn wider.
The ideal current source produces a defined constant output current $I_s$ (in German often $I_q$ for Quellenstrom).
For this current to flow, any voltage can be applied to its terminals.
The current-voltage characteristic also represents this (see Abbildung 4).
The circuit symbol shows again a circle with two connections. This time the two connections are left open in the circle and a line is drawn perpendicular to them.
wire connection
- The ideal connection line is resistance-free and transmits current and voltage instantaneously.
- Real existing influences (e.g. voltage drop) of connections are considered via separately drawn components (e.g. ohmic resistance).
2.2 Reference-arrow Systems and first consideration of a DC circuit
Goals
After this lesson you should:
- Be able to apply and distinguish between the producer and consumer reference arrow systems.
In the chapter 1. Preparation and Proportions the conventional directional sense of currents and voltages has already been discussed. Unfortunately, with meshed networks it is often not clear ahead of the calculation in which direction the conventional sense of direction of all currents and voltages runs.
In Abbildung 5 such a meshed net is shown. In this circuit a switch $S_1$ and a current $I_2$ are marked. Once the state of the switch is swapped, the direction of the current changes.
Generator and Load (Reference) Arrow System
For the direction of the arrows different conventions are available. Here (and quite often in Germany) the convention of power engineering is used. This convention is
Generator Reference Arrow System
With sources (or generators), energy is taken from the environment and made available to the circuit.
For generators, the arrowfoot of the current is attached to the arrowhead of the voltage. Voltage and current arrows are antiparallel ($\uparrow \downarrow$).
For generators holds: $P_{1} = U_{12} \cdot I_1 \stackrel{!}{>} 0$
The power transfer from the environment to the power system via the generator or the generator arrow system is calculated positively.
Load Reference Arrow System
In the case of consumers, energy is taken from the circuit and made available to the environment.
For consumers, the arrowfoot or arrowhead of the current and voltage are related. Voltage and current arrows are parallel ($\uparrow \uparrow$).
For consumers, the following holds:
$P_{3} = U_{34} \cdot I_3 \stackrel{!}{>} 0$
The power transfer from the power system to the environment via the consumer or the consumer arrow system is also calculated positively.
Note:
- Before the calculation, the reference arrows for currents and voltages are set arbitrarily, with the following conditions:
- the generator arrow system - current antiparallel to the voltage arrow - is used for all sources (e.g. all voltage and current sources)
- the motor arrow system - current parallel to the voltage arrow - is used for all consumers (e.g. all passives like resistors, capacitors, inductors, diodes etc.)
- for loads, where the direction of the power is not known, the motor arrow system is recommented (e.g. passives, in case what these are part of a machine, like inductors of a motor)
- After the calculation means
- $I>0$: The reference arrow reflects the conventional directional sense of the current
- $I<0$: The reference arrow points in the opposite direction to the conventional directional sense of the current
- Reference arrows of the current are drawn in the wire if possible.
The reference arrow system
2.3 Nodes, Branches and Loops
Explanation of the different network structures
(Graphs and trees are only needed in later chapters)
Goals
After this lesson you should:
- Be able to identify the nodes, branches and loops in a circuit.
- Be able to use them to make a circuit clearer.
Electrical circuits typically have the structure of networks. Networks consist of two elementary structural elements:
- Branches (German: Zweige): Connections between two nodes
- Node (German: Knoten): Connection points of several branches
Please note in the case of electrical circuits:
- Branches contain at least one component.
- Nodes connect more than two branches and can also be spatially extended.
Branches in electrical networks are also called two-pole. Their behaviour is described by current-voltage characteristics and explained in more detail in the chapter non-ideal_sources_and_two_pole_networks .
In addition, another term is to be explained:
A loop is a closed path in the mesh. This means that a loop begins and ends at the same node and runs over at least one further node.
Since a voltmeter can also be present as a component between two nodes, it is also possible to close a loop by a drawn voltage arrow (cf. $U_1$ in Abbildung 10).
Please keep in mind, that usually the entire behaviour of networked circuits almost always changes when a change occurs in one branch or at one node. This is in contrast to other cause-effect relationships, but comparable to changes in other larger networks, e.g. a traffic jam in the road network, due to which other roads experience a higher load. For electrical engineering, this means that in the case of changing circuits, the focus is often on determining the interrelationships (formulas, current-voltage characteristics) and not on a single numerical value.
Simplifications
With the knowledge of nodes, branches and meshes, circuits can be simplified. Circuits can be reshaped arbitrarily as long as all branches remain at the same nodes after reshaping The Abbildung 11 shows how such a transformation is possible.
For practical tasks, repeated trial and error can be useful. It is important to check afterwards that the same components are connected to each node as before the transformation.
Further examples can be found in the following video
Exercise 2.3.1 Branches and Nodes
For the markings in the circuits in Abbildung 12 indicate whether it is a branch, a node, or neither.
Exercise 2.3.2 Simplifications of circuits
Simplify the circuits in Abbildung 13.
2.4 Kirchhoff's circuit laws
Representation and application of Kirchhoff's circuit laws
Goals
After this lesson you should: Know and be able to apply Kirchhof's circuit laws (Kirchhoff's current law andKirchhoff's voltage law).
Kirchhoff's current law (Kirchhoff's first law)
The Kirchhoff's current law (Kirchhoff's nodal rule, in German: Knotensatz) formulates in the language of mathematics the experience that no charge „accumulations“ occur in electrical wires. This is of particular relevance at a network node (Abbildung 14). To formulate the equation at this node, the reference arrows of the currents are all set in the same way. That means: all point away from or towards the node.
Note:
The sum of all currents flowing from the nodes must be zero.
$\boxed{I_1 + I_2 + I_3 + ... + I_n = \sum_{x=1}^{n} I_x=0}$
From now on, the following definition applies:
- Currents whose current arrows point towards the node are added in the calculation.
- Currents whose current arrows point away from the node are subtracted in the calculation.
Parallel connection of resistors
From the Kirchhoff's current law, the total resistance for resistors connected in parallel can be derived (Abbildung 15):
Since the same voltage $U_{ab}$ is dropped across all resistors, using the Kirchhoff's current law:
$\large{{U_{ab}}\over{R_1}}+ {{U_{ab}}\over{R_2}}+ ... + {{U_{ab}}\over{R_n}}= {{U_{ab}}\over{R_{substitute}}$
$\rightarrow \large{{{1}\over{R_1}}+ {{1}\over{R_2}}+ ... + {{1}\over{R_n}}= {{1}\over{R_{substitute}} = \sum_{x=1}^{n} {{1}\over{R_x}}$
Thus, for resistors connected in parallel, the equivalent conductance $G_{eq}$ (German: Ersatzleitwert) is the sum of the individual conductances: $G_{eq} = \sum_{x=1}^{n} {G_x}$
In general: the equivalent resistance of a parallel circuit is always smaller than the smallest resistance.
Especially for two parallel resistors $R_1$ and $R_2$ applies: $R_{eq}= \large{{R_1 \cdot R_2}\over{R_1 + R_2}}$
Current divider
Derivation of the current divider with further considerations
The current divider rule can also be derived from the Kirchhoff's current law.
This states that, for resistors $R_1, ... R_n$ their currents $I_1, ... I_n$ behave just like the conductances $G_1, ... G_n$ through which they flow.
$\large{{I_1}\over{I_g}} = {{G_1}\over{G_g}}$
$\large{{I_1}\over{I_2}} = {{G_1}\over{G_2}}$
Exercise 2.4.1 Current divider
In the simulation in Abbildung 16 a current divider can be seen. The resistances are just inversely proportional to the currents flowing through it.
- What currents would you expect in each branch if the input voltage were lowered from $5V$ to $3.3V$? After thinking about your result, you can adjust the
Voltage(bottom right of the simulation) accordingly by moving the slider. - Think about what would happen if you flipped the switch before you flipped the switch.
After you flip the switch, how can you explain the current in the branch?
Exercise 2.4.2 two resistors
Two resistors of $18\Omega$ and $2 \Omega$ are connected in parallel. The total current of the resistors is $3A$.
Calculate the total resistance and how the currents is split to the branches.
Kirchhoff's voltage law (Kirchhoff's second law)
Also the Kirchhoff's voltage law describes in mathematical language another practical experience: Between two points $1$ and $2$ of a network there is only one potential difference. Thus the potential difference is in particular independent of the way a network is traversed between the two points $1$ and $2$. This can be described by considering the meshes.
Note:
In any mesh of an electrical circuit, the sum of all voltages is always zero (Abbildung 17):
$\boxed{U_{1} + U_{2} + ... + U_{n} = \sum_{x=1}^{n} U_x = 0}$
To calculate this, a sense of orbit must be specified. This can be chosen arbitrarily at first. However, the following specification then applies: Stresses whose stress arrows point in the direction of circulation are added in the calculation. Stresses whose arrows point against the direction of rotation are subtracted in the calculation.
Zur Berechnung muss ein Umlaufsinn festgelegt werden. Diese kann zunächst beliebig gewählt werden. Es gilt dann aber folgende Festlegung:
- Spannungen, deren Spannungspfeile im Umlaufsinn zeigen, werden in der Rechnung addiert.
- Spannungen, deren Spannungspfeile gegen Umlaufsinn zeigen, werden in der Rechnung subtrahiert.
Beweis des Maschensatzes
Drückt man die Spannungen in Abbildung 17 durch die Potentiale in den Knotenpunkten aus, so ergibt sich:
$U_{12}= \varphi_1 - \varphi_2 $
$U_{23}= \varphi_2 - \varphi_3 $
$U_{34}= \varphi_3 - \varphi_4 $
$U_{41}= \varphi_4 - \varphi_1 $
Werden diese Spannungen in die Maschengleichung eingesetzt, so wird
$U_{12}+U_{23}+U_{34}+U_{41} = 0$
Reihenschaltung von Widerständen
Über den Maschensatz lässt sich der Gesamtwiderstand einer Reihenschaltung (<imref BildNr13>) leicht ermitteln:
$U_1 + U_2 + ... + U_n = U_g$
$R_1 \cdot I_1 + R_2 \cdot I_2 + ... + R_n \cdot I_n = R_{ersatz} \cdot I $
Da bei der Reihenschaltung der Strom durch alle Widerstände gleich sein muss - also $I_1 = I_2 = ... = I$ - ergibt sich:
$R_1 + R_2 + ... + R_n = R_{ersatz} = \sum_{x=1}^{n} R_x $
Allgemein gilt: Der Ersatzwiderstand einer Reihenschaltung ist stets größer als der größte Widerstand.
Exercise 2.4.3 drei Widerstände
Gegeben sind drei gleiche Widerstände mit je $20k\Omega$.
Welche Werte sind durch beliebige Verschaltung von einem bis drei Widerstände realisierbar?
2.5 unbelasteter und belasteter Spannungsteiler
Der unbelastete Spannungsteiler
Herleitung des unbelasteten Spannungsteilers
Ziele
Nach dieser Lektion sollten Sie:
- den belasteten und unbelasteten Spannungsteiler auseinanderhalten können.
- die Unterschiede zwischen belasteten und unbelasteten Spannungsteiler beschreiben können.
Speziell die Hintereinanderschaltung von zwei Widerständen $R_1$ und $R_2$ soll nun näher betrachtet werden. Diese Situation tritt in vielen praktischen Anwendungen auf (z.B. Potentiometer). In Abbildung 21 ist diese Schaltung dargestellt.
Über die Maschengleichung ergibt sich
$\boxed{ {{U_1}\over{U}} = {{R_1}\over{R_1 + R_2}} }$
Das Verhältnis $k={{R_1}\over{R_1 + R_2}}$ entspricht auch der Position an einem Potentiometer.
Exercise 2.5.1 unbelasteter Spannungsteiler
In der Simulation in Abbildung 22 ist ein unbelasteter Spannungsteiler in Form eines Potentiometers zu sehen. Die ideale Spannungsquelle stellt $5V$ bereit. Das Potentiometer hat einen Gesamtwiderstand von $1K\Omega$. In der dargestellten Konfiguration ist dieser auf $500 \Omega$ und $500 \Omega$ ausgeteilt.
- Welche Spannung
U_outerwarten Sie, wenn der Schalter geschlossen würde? Nachdem Sie Ihr Ergebnis überlegt hatten, können Sie dieses durch Schließen das Schalters überprüfen. - Überlegen Sie sich zunächst was passiert wenn Sie durch Verschieben des Schleifers („Zwischenabgriff“) die Aufteilung der Widerstände verändern würden?
Durch den Slider unten rechts neben der Simulation lässt sich Ihre Vermutung überprüfen. - Bei welcher Stellung erhalten Sie ein
U_outvon $3,5V$?
Der belastete Spannungsteiler
Wird - im Gegensatz zum obigen, unbelasteten Spannungsteiler - an den Ausgangsklemmen eine Last $R_L$ angeschlossen (Abbildung 23), so beeinflusst diese die Ausgangsspannung.
Durch eine Schaltungsanalyse ergibt sich:
$ U_1 = \LARGE{{{U} \over {1 + {{R_2}\over{R_L}} + {{R_2}\over{R_1}} }} }$
bzw. an einem Potentiometer mit $k$ und $R_s = R_1 + R_2$:
$ U_1 = \LARGE{{{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}} }} }$
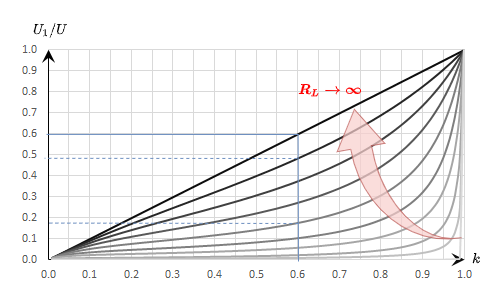
Abbildung 24 zeigt in welchem Verhältnis die ausgegebene Spannung $U_1$ zur eingehenden Spannung $U$ steht (y-Achse), in Bezug zum Verhältnis $k={{R_1}\over{R_1 + R_2}}$. Prinzipiell gleicht dies der Abbildung 21, hat aber hier noch eine weitere Dimension: Es sind mehrere Graphen eingezeichnet. Diese unterscheiden sich um das Verhältnis ${{R_s}\over{R_L}}$.
Was sagt dieses Diagramm nun aus? Dies soll an einem Beispiel gezeigt werden. Zunächst wird angenommen, dass ein unbelasteter Spannungsteiler mit $R_2 = 4 k\Omega$ und $R_1 = 6 k\Omega$, sowie eine Eingangsspannung von $10V$ vorliegt. Damit ist $k = 0,6$, $R_s = 10k\Omega$ und $U_1 = 6V$.
Nun wird dieser Spannungsteiler mit einem Lastwiderstand belastet. Liegt dieser bei $R_L = R_1 = 10 k\Omega$, so reduziert sich $k$ auf etwa $0,48$ und $U_1$ auf $4,8V$ - die Ausgangsspannung bricht also ein. Bei $R_L = 4k\Omega$ wird $k$ noch kleiner zu $k=0,375$ und $U_1 = 3,75V$. Ist die Last $R_L$ nur noch ein Zehntel des Widerstandes $R_s=R_1 + R_2$, so wird $k=0,18$ und $U_1=1,8V$. Aus der Ausgangspannung des unbelasteten Spannungsteilers ($6V$) wurde damit weniger als ein Drittel.
Exercise 2.5.2 belasteter Spannungsteiler
Ermitteln Sie aus der Schaltung in Abbildung 23 die obige Gleichung $ U_1 = {{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}}}}$ mit $k={{R_1}\over{R_1 + R_2}}$ und $R_s = R_1 + R_2$.
Exercise 2.5.3 belasteter Spannungsteiler
In der Simulation in Abbildung 25 ist ein belasteter Spannungsteiler in Form eines Potentiometers zu sehen. Die ideale Spannungsquelle stellt $5V$ bereit. Das Potentiometer hat einen Gesamtwiderstand von $1K\Omega$. In der dargestellten Konfiguration ist dieser auf $500 \Omega$ und $500 \Omega$ ausgeteilt. Der Lastwiderstand hat eine Größe von $R_L = 1 k\Omega$.
- Welche Spannung
U_OUTerwarten Sie, wenn der Schalter geschlossen würde? Hier müssen Sie etwas rechnen! Nachdem Sie Ihr Ergebnis berechnet hatten, können Sie dieses durch Schließen das Schalters überprüfen. - Bei welcher Aufteilung erhalten Sie $3,5V$. Ermitteln Sie das Ergebnis zunächst zur eine Rechnung.
Überprüfen sie es anschließend durch Verschieben des Slider unten rechts neben der Simulation.
Exercise 2.5.4 Anwendung des belasteten Spannungsteilers - Motor
Sie wollten einen Kleinstmotor für einen kleinen Roboter testen. Anhand des Maximalstroms und des Innenwiderstands ($R_M = 5\Omega$) errechnen Sie, dass dieser mit maximal $U_{M,max}=4V$ betrieben werden kann. Ein Kollege meinte, dass Sie $4V$ über den Aufbau in Abbildung 26 aus einer $9V$-Block Batterie erhalten können.
- Berechnen Sie zunächst den Maximalstrom $I_{M,max}$ des Motors.
- Zeichnen Sie die entsprechende elektrische Schaltung mit angeschlossenem Motor als ohmschen Widerstand.
- Beim Maximalstrom soll der Motor ein Drehmoment von $M= 100mNm$ abgeben können. Welches Drehmoment würde der Motor abgeben, wenn Sie den Aufbau so umsetzen? (Annahme: Das Drehmoment des Motors steigt proportional zum Motorstrom).
- Wie könnte ein Aufbau mit Potentiometer aussehen, mit dem man tatsächlich eine Spannung zwischen $0,5V$ bis $4V$ am Motor einstellen kann? Welchen Widerstandswert muss das Potentiometer haben?
- Bauen Sie Ihre Schaltung in untenstehender Simulation auf und testen Sie diese. Eine Einführung zur Online-Simulation finden Sie unter: Online Circuit Simulator.
Für diesen Aufbau benötigen Sie im wesentlichen folgende Tipps:- Das Verlegen von Verbindungen lässt sich über das Menü
Zeichnen » Verbindung einfügen (wire)aktivieren. Anschließend muss auf den Startpunkt geklickt und anschließend bis zum Endpunkt gezogen werden. - Beachten Sie, dass Verbindungen immer nur an Verbindungspunkten angeschlossen werden können. Der rot markierte Knoten am $5 \Omega$-Widerstand zeigt an, dass dieser nicht verbunden ist. Dieser könnte im ein Rasterschritt nach links verschoben werden, da dort ein Verbindungspunkt liegt.
- Mit Druck auf die
<ESC>Taste lässt sich das Einfügen von Komponenten deaktivieren. - Mit Rechtsklick auf eine Komponente lässt sich diese kopieren oder Werte wie der Widerstand über
Bearbeiten…ändern.
Exercise 2.5.5 Beispiele der Berechnung von belasteten Spannungsteilern
Spannungsteiler, Vorwiderstand (Längswiderstand) und Nebenwiderstand
Übung zum Spannungsteiler
Exercise 2.5.6 Beispiel eines belasteten Spannungsteiler: Erklärung ohne Rechnung
2.6 Stern-Dreieck-Schaltung
Ziele
Nach dieser Lektion sollten Sie:
- dreieckige Maschen in eine Sternform (und umgekehrt) umwandeln können
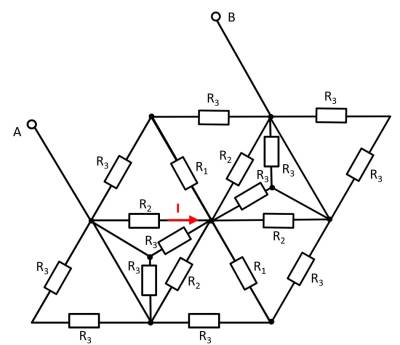
Zu Beginn des Kapitels wurde ein Beispiel eines Netzwerks gezeigt (Abbildung 1). Dabei kommt man aber mit dem Knoten- und Maschensatz nicht unmittelbar zur Lösung. Jedoch ist nach sichtbar, dass dort viele dreieckförmige Maschen bzw. sternförmige Knoten vorhanden sind (Abbildung 28). Auf diese soll nun tiefer eingegangen werden.
Dazu zunächst ein Resume aus den bisherigen Erkenntnissen. Über den Knoten- und Maschensatz wurde klar, dass sowohl aus einer Reihen-, als auch aus einer Parallelschaltung ein Ersatzwiderstand ermittelt werden kann. Betrachtet man den Ersatzwiderstand als eine Blackbox - d.h. der innere Ausbau ist unbekannt - so könnte dieser also durch beide Schaltungsarten interpretiert werden (Abbildung 29).
Wie hilft uns das nun im Falle einer dreieckförmigen Masche?
Auch in für diesen Fall kann man eine Blackbox bereitstellen. Diese müsste sich aber immer gleich verhalten, wie die dreieckförmige Masche, also beliebige, angelegte Spannungen sollten gleiche Ströme erzeugen.
Anders gesagt: Die zwischen zwei Klemmen messbaren Widerständen müssen für beide Schaltungen identisch sein.
Dazu sollen nun die verschiedenen Widerstände zwischen den einzelnen Knoten $a$, $b$ und $c$ betrachtet werden, siehe Abbildung 30. Es soll herausgefunden werden wie aus einer Stern-Schaltung eine Dreieck-Schaltung entwickelt werden kann (und umgekehrt).
Abb. 30: Stern-Dreieck-Transformation
Berechung der Umformungsformeln: Sternschaltung in Dreiecksschaltung
Dreieckschaltung
Bei der Dreieckschaltung sind die 3 Widerstände $R_{ab}^1$, $R_{bc}^1$ und $R_{ca}^1$ in einer Masche verschalten.
Für die Widerstände zwischen den zwei Anschlüssen (z.B. $a$ und $b$) wird die dritte ($c$) als nicht angeschlossen betrachtet. Damit ergibt sich eine Parallelschaltung des direkten Sternwiderstands $R_{ab}^1$ mit der Reihenschaltung der anderen beiden Sternwiderstände $R_{ca}^1 + R_{bc}^1$:
$R_{ab} = R_{ab}^1 || (R_{ca}^1 + R_{bc}^1) $
$R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + (R_{ca}^1 + R_{bc}^1)}} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} $
Gleiches gilt für die anderen Anschlüssen. Damit ergibt sich:
\begin{align*} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \tag{2.6.1} \end{align*}
Sternschaltung
Die Widerstände zwischen den Anschlüssen müssen nun denen bei der Sternschaltung gleichen. Auch bei der Sternschaltung sind 3 Widerstände verschalten, diese aber in Sternform. Die Sternwiderstände sind also alle mit einem weiteren Knoten $0$ in der Mitte verbunden: $R_{a0}^1$, $R_{b0}^1$ und $R_{c0}^1$
Auch hier wird vorgegangen wie bei der Dreieckschaltung: der Widerstand zwischen zwei Anschlüssen (z.B. $a$ und $b$) wird ermittelt, der weitere Anschluss ($c$) wird als offen betrachtet. Der Widerstand des weiteren Anschlusses ($R_{c0}^1$) ist nur an einer Seite angeschlossen. Dadurch fließt durch diesen kein Strom - er ist damit nicht zu berücksichtigen. Es ergibt sich:
\begin{align*} R_{ab} = R_{a0}^1 + R_{b0}^1 \\ R_{bc} = R_{b0}^1 + R_{c0}^1 \\ R_{ca} = R_{c0}^1 + R_{a0}^1 \tag{2.6.2} \end{align*}
Aus den Gleichungen $(2.6.1)$ und $(2.6.2)$ erhält man:
\begin{align} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{a0}^1 + R_{b0}^1 \tag{2.6.3} \end{align} \begin{align} R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{b0}^1 + R_{c0}^1 \tag{2.6.4} \end{align} \begin{align} R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{c0}^1 + R_{a0}^1 \tag{2.6.5} \end{align}
Die Gleichungen $(2.6.3)$ bis $(2.6.5)$ lassen sich nun so geschickt zusammenfassen, dass auf einer Seite nur noch ein Widerstand steht.
Eine Variante ist die Formeln als ${{1}\over{2}} \cdot \left( (2.6.3) + (2.6.4) - (2.6.5) \right)$ bzw. ${{1}\over{2}} \cdot \left(R_{ab} + R_{bc} - R_{ca}\right)$ zu kombinieren. Damit ergibt sich $R_{b0}^1$
\begin{align*} {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} + {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} - {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( R_{a0}^1 + R_{b0}^1 + R_{b0}^1 + R_{c0}^1 - R_{c0}^1 - R_{a0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)} + {R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)} - {R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( 2 \cdot R_{b0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 R_{ca}^1 + R_{ab}^1 R_{bc}^1 + R_{bc}^1 R_{ab}^1 + R_{bc}^1 R_{ca}^1 - R_{ca}^1 R_{bc}^1 - R_{ca}^1 R_{ab}^1}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{1}\over{2}} \cdot \left( {{ 2 \cdot R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{ R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} &= R_{b0}^1 \\ \end{align*}
Auf ähnlichem Weg kann man nach $R_{a0}^1$ und $R_{c0}^1$, sowie mit etwas abgewandeltem Ansatz auch auf $R_{ab}^1$, $R_{bc}^1$ und $R_{ca}^1$ auflösen.
Stern-Dreieck-Transformation
Merke:
Soll von einer Dreieckschaltung in eine Sternschaltung umgewandelt werden, so sind die Sternwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{an Anschluss x} \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Produkt der} \\ \text{am Anschluss x liegenden} \\ \text{Dreieckwiderstände} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller} \\ \text{Dreieckwiderstände} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{a0}^1 &= {{ R_{ca}^1 \cdot R_{ab}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{b0}^1 &= {{ R_{ab}^1 \cdot R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{c0}^1 &= {{ R_{bc}^1 \cdot R_{ca}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \end{align*}
Soll von einer Sternschaltung in eine Dreieckschaltung umgewandelt werden, so sind die Dreieckwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Dreieckwiderstand} \\ \text{zwischen den} \\ \text{Anschlüssen x und y } \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller Produkte} \\ \text{zwischen zwei} \\ \text{unterschiedlichen Sternwiderständen} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{gegenüber von x und y} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{ab}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{c0}^1}} \\ R_{bc}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{a0}^1}} \\ R_{ca}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{b0}^1}} \end{align*}
Exercise 2.6.1 Anwendung der Dreieck-Stern-Umwandlung
Exercise 2.6.2 schwierigere Aufgabe mit Stern-Dreieck-Umwandlung
2.7 Gruppenschaltung von Widerständen
Ziele
Nach dieser Lektion sollten Sie:
- Schaltungen, welche nur aus Widerständen bestehen, vereinfachen können.
- die Spannungen und Ströme in Schaltungen mit einer Spannungsquelle und mehreren Widerständen berechnen können.
- symmetrische Schaltungen vereinfachen können.
In diesem Unterkapitel wird auf eine Methodik eingegangen, welche beim Umformen von Schaltungen helfen soll. In Unterkapitel 2.6 Stern-Dreieck-Schaltung wurde gegen Ende bereits ein Netzwerk so umgeformt, dass es keine dreieckigen Maschen mehr enthält. Nun soll dieses Vorgehen systematisiert werden. Ausgangspunkt sind Aufgaben, bei denen für ein Widerstandsnetzwerk der Gesamtwiderstand, Gesamtstrom oder die Gesamtspannung berechnet werden muss.
einfaches Beispiel
Ein Beispiel für eine solche Schaltung ist in Abbildung ## gegeben. Hier ist $I_0$ gesucht. Dieser Strom kann über die (gegebene) Spannung $U_0$ und den Gesamtwiderstand zwischen den Klemmen $a$ und $b$ ermittelt werden. Gesucht ist also $R_{ab}$.
Wie bereits in den vorherigen Unterkapitel beschrieben, können hier auch Teilschaltung schrittweise in Ersatzwiderstände umgewandelt werden. Wichtig dabei ist, dass diese Teilschaltungen zur Umwandlung in Ersatzwiderstände immer nur zwei Anschlüsse (= zwei Knoten zur „Außenwelt“) haben dürfen.
Abbildung ## zeigt die schrittweise Umwandlung der Ersatzwiderstände an diesem Beispiel.
Als Ergebnis des Ersatzwiderstands erhält man:
\begin{align*} R_g = R_{12345} &= R_{12}||R_{345} = R_{12}||(R_3+R_{45}) = (R_1||R_2)||(R_3+R_4||R_5) \\ &= {{ {{R_1 \cdot R_2}\over{R_1 + R_2}} \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) }\over{ {{R_1 \cdot R_2}\over{R_1 + R_2}} +R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}} }} \quad \quad \quad \quad \quad \quad \bigg\rvert \cdot{{(R_1 + R_2) \cdot (R_4 + R_5)}\over{(R_1 + R_2) \cdot (R_4 + R_5)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) \cdot (R_4 + R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 \cdot (R_4 + R_5) + R_4 \cdot R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ \end{align*}
Beispiel mit Dreieck-Stern-Transformation
Mit der Dreieck-Stern-Transformation lässt sich nun auch das anfängliche Beispiel umwandeln. Bei komplizierteren Schaltungen ist die wiederholte Dreieck-Stern-Transformation mit anschließendem Zusammenfassen der Widerstände sinnvoll, solange bis die entstandene Schaltung leicht mit Knoten- und Maschensatz berechenbar wird (Abbildung ##). Hier wird auf eine Rechnung verzichtet - es empfiehlt sich hier mit Zwischenergebnissen für die transformierten Widerständen zu rechnen.
Beispiel mit Symmetrien in der Schaltung
Ein gewisser Sonderfall betrifft mögliche Symmetrien in Schaltungen. Falls dies3 vorhanden sind, kann eine weitere Vereinfachung vorgenommen werden.
Abbildung ## zeigt links ein symmetrischen Aufbau eines Netzwerks aus jeweils gleichen Widerständen $R$. Zum Verständnisgewinn ist in der Mitte in der gleichen Schaltung zusätzlich Schalter und Testpunkte (TP) verbaut, welche die Spannung gegen Masse anzeigen.
Über die Schalter kann nachgeprüft werden, ob ein Strom fließt, falls die jeweiligen Knoten verbunden werden. In der Simulation ist zu sehen, dass dies nicht der Fall ist. Im symmetrischen Aufbau sind diese Knoten jeweils auf dem gleichen Potential.
Damit lässt sich die Schaltung auch in die Form bringen, wie sie in Abbildung ## rechts zu sehen ist. Diese Schaltung ist wiederum leicht berechenbar:
\begin{align*} R_g = R || R + R || R || R || R + R || R || R || R + R || R = {{1}\over{2}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{2}}\cdot R = 1,5\cdot R \end{align*}
Exercise 2.7.1 Aufgabe zur Schaltungsvereinfachung I
Exercise 2.7.2 Aufgabe zur Schaltungsvereinfachung II + III
Exercise 2.7.3 Aufgabe zur Schaltungsvereinfachung IV
Exercise 2.7.4 Aufgabe zur Schaltungsvereinfachung IV
Exercise 2.7.5 Aufgabe zur Schaltungsvereinfachung V
Exercise 2.7.6 Aufgabe zur Schaltungsvereinfachung VI
Exercise 2.7.7 Simplifying Circuits (exam task, about 8% of a 60-minute exam, WS2020)
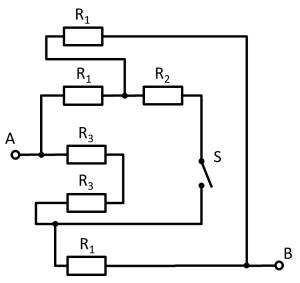
Given is the adjoining circuit with
$R_1=10 ~\Omega$
$R_2=20 ~\Omega$
$R_3=5 ~\Omega$
and the switch $S$.
1. Determine the total resistance $R_{\rm eq}$ between A and B by summing the resistances with the switch $S$ open.
- How can the circuit be better represented or pulled apart?
- The switch should be replaced by an open wire in this case.
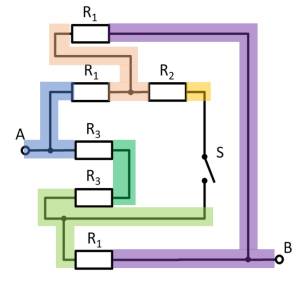
For this purpose, the individual branches can be highlighted in color and interpreted as a „conductive rubber band“.
This results in:
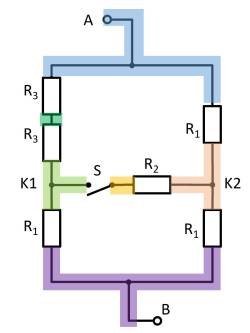
Thus $R_3$ and $R_3$ can be combined to $R_{33} = 2 \cdot R_3 = R_1$, yielding a left and a right voltage divider.
Now it is visible that in the left and right voltage divider, the same potential is at the respective branch, or at the node K1 (green) and K2 (pink).
Thus, the total resistance can be calculated as $R_{\rm eq} = (2 \cdot R_1)||(2 \cdot R_1)$.
However, by symmetry, nodes K1 and K2 can also be short-circuited. Thus, $R_{\rm eq} = 2 \cdot \left( R_1||R_1 \right)$ also holds.
2. What is the total resistance when switch $S$ is closed?
So the resistance remains the same.
Exercise 2.7.8: Simplifying Circuits II (written exam task, approx 8% of a 60-minute written exam, WS2020)
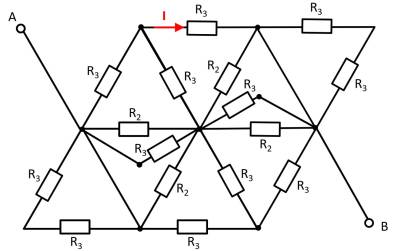
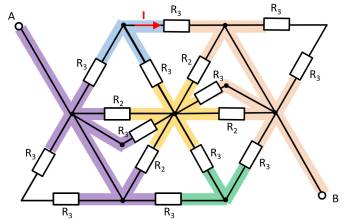
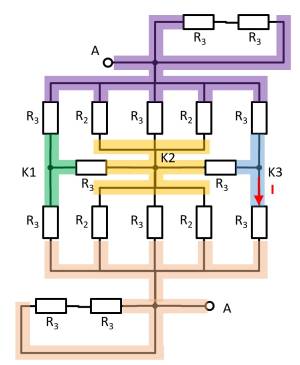
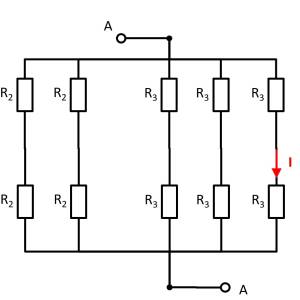
Given is the adjoining circuit with
$R_1=5 ~\Omega$
$R_2=10 ~\Omega$
$R_3=20 ~\Omega$
1. Determine the equivalent resistance $R_{\rm eq}$ between A and B by summing the resistances.
- How can the circuit be better represented or pulled apart?
- Switches (when used) should be replaced by an open or closed circuit.
- Does this result in equal potentials at different nodes that can be cleverly used?
For this purpose, the individual branches can be highlighted in color and interpreted as a „conductive rubber band“.
It can be seen that the two resistors $R_3$ at the top left and bottom right are each shorted. The result is thus:
Here it helps to consider the potential of the nodes K1, K2, and K3. For K2, the resistances $R_2 || R_3 || R_2$ must be combined at the top and bottom. Thus, the same resistance values at the top and bottom result. Also at the nodes K1 and K2 the same resistance values at the top and at the bottom result. With the same ratios of the resistances at K1, K2, and K3 respectively, it can be concluded that no current flows across the resistors $R_3$ between K1 and K2 or K2 and K3. Thus, these do not contribute to the total resistance. In such a case, a short circuit or an open line can be freely chosen between the relevant nodes for the calculation. In the following, an open line is chosen. Additionally, the parallel strings can be reordered.
This results in:
\begin{align*} R_{\rm eq} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) && || \; \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{\rm eq} &= R_2 && || \;\frac{2}{3}\cdot R_3 \\ R_{\rm eq} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} \\ R_{\rm eq} &= \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Now let the voltage from A to B be: $U_{AB}=U_0= 20 ~\rm V$. What is the current $I$?
Exercise 2.7.9 - Variation: Simplifying Circuits II (written exam task, approx 8% of a 60-minute written exam, WS2020)
Given is the adjoining circuit with
$R_1=10 ~\Omega$
$R_2=20 ~\Omega$
$R_3=5 ~\Omega$
1. Determine the equivalent resistance $R_{\rm eq}$ between A and B by summing the resistances.
2. Now let the voltage from A to B be: $U_{\rm AB}=U_0= 10 ~\rm V$. What is the current $I$?
Exercise 2.7.10 - Variation: Simplifying Circuits III (written exam task, approx 8% of a 60-minute written exam, WS2020)
weitere Exercises
Weitere Anfgaben sind Online auf den Seiten von HErTZ zu finden (Auswahl links im Menu).