Musterlösung Wintersemester 2020/2021
Aufgabe 5.4.2 Feldstärke in unterschiedlicher Geometrie I (Klausuraufgabe, ca 6% einer 60minütigen Klausur)
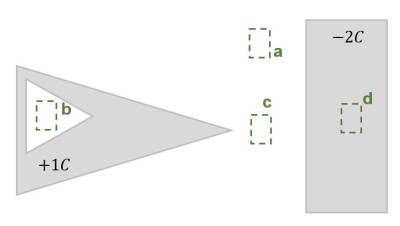
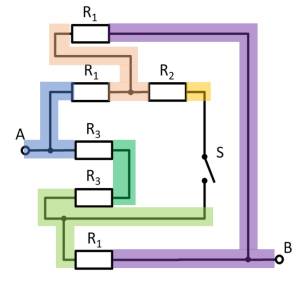
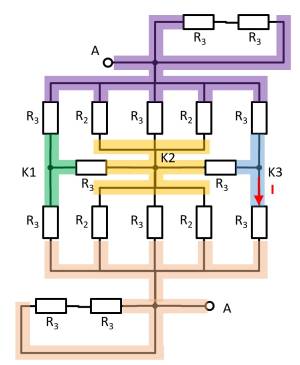
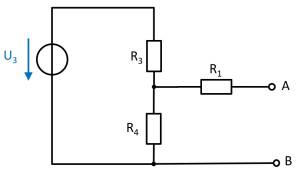
In der Abbildung rechts ist eine Anordnung aus idealen metallischen Leitern (grau) mit angegebener Ladung gezeigt. In weiß ist ein Dielektrikum (z.B. Vakuum) dargestellt. Mehrere, bezeichnete Bereiche sind durch grün gestrichelte Rahmen eingezeichnet, welche sich teilweise im Innern der Objekte befinden.
Ordnen Sie die bezeichneten Bereiche eindeutig nach aufsteigender Feldstärke (Betrag)! Geben Sie auch an, wenn bezeichneten Bereiche betragsmäßig die gleiche Feldstärke haben.
- Welches Feld herrscht in einem Raum vor, der vollständig durch einen leitfähigen Leiter umgeben wird?
- Wie verhält sich das Feld im Inneren eines Leiters?
- Erhöht oder sinkt die Feldstärke, wenn sich eine Ladung sich von einer anderen Ladung wegbewegt?
- Ist das Feld an bei einer Spitze höher oder niedriger?
- Bei $b$ und $d$ ist kein Feld messbar, da der umgebene Leiter auf einem konstanten Feld liegt. Er ergibt sich keine Potentialdifferenz und damit auch kein Feld.
- Bei $c$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt. Durch die Spitze kommt es zu einer Ladungsüberhöhung und damit zu einem höheren Feld.
- Bei $a$ ist ein Feld (Betrag >0) messbar, welches von der Ladung ($+1C$) zum länglichen Leiter ($-2C$) hinzeigt.
Aufgabe 5.1.3 Kräfte auf Ladungen (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
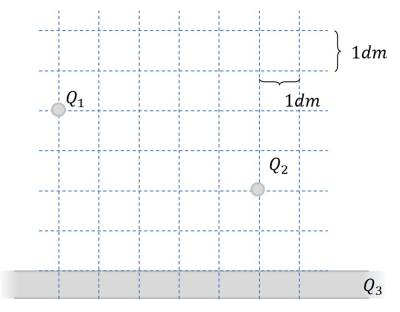
Gegeben ist eine im Vakuum befindliche Anordnung elektrischer Ladungen (siehe Bild rechts).
Die Ladungen haben folgende Werte:
$Q_1=7 μC$ (Punktladung)
$Q_2=5 μC$ (Punktladung)
$Q_3=0 C$ (unendlich ausgedehnte Flächenladung)
$\varepsilon_0=8,854\cdot 10^{-12} F/m$ , $\varepsilon_r=1$
1. Berechnen Sie Betrag der Kraft von $Q_2$ auf $Q_1$, ohne die Kraftwirkung von $Q_3$.
- Welche Gleichung ist für die Kraftwirkung von Ladungen anzuwenden?
- Wie lässt sich der Abstand zwischen den beiden Ladungen ermitteln?
2. Ist diese Kraft anziehend oder abstoßend?
- Welche Kraftwirkung zeigen gleich bzw. gegensätzlich geladene Körper aufeinander?
3. Nun sei $Q_2=0$ und die Flächenladung $Q_3$ in der Art gestaltet, dass sich ein homogenes elektrisches Feld mit $E_3=100 kV/m$ ergibt.
Welche Kraft (Betrag) ergibt sich nun auf $Q_1$?
- Welche Gleichung ist für die Kraftwirkung im homogenen Feld anzuwenden?
Aufgabe 5.2.1 mehrere Kräfte auf eine Ladung I (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
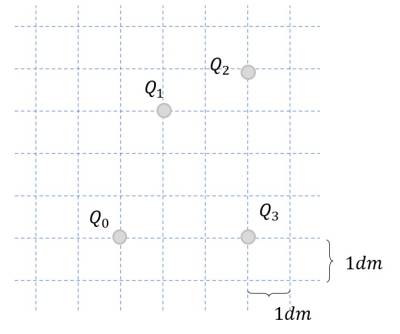
Gegeben ist die die Anordnung elektrischer Ladungen im Bild rechts.
Es ergeben sich folgende Kraftwirkungen:
$F_{01}=-5 N$
$F_{02}=-6 N$
$F_{03}=+3 N$
Ermitteln Sie rechnerisch die den Betrag der resultierenden Kraft.
- Wie müssen die Kräfte vorbereitet werden, dass sie tatsächlich addiert werden können?
Die vorhandenen Kräfte müssen in Koordinaten zerlegt werden. Hier empfehlen sich die orthogonalen Koordinaten ($x$ und $y$).
Das Koordinatensystem sei so ausgelegt, dass der Ursprung in $Q_0$ liegt mit der x-Achse in Richtung Q_3 und die y-Achse entsprechend rechtwinklig dazu.
Zur Koordinatenzerlegung sind die Winkel $alpha_{0n}$ der Kräfte zur x-Achse notwendig.
Diese ergeben sich im gewählten Koordinatensystem aus den Koordinaten der Ladungen: $\alpha_{0n} = atan(\frac{\Delta y}{\Delta x})$
$\alpha_{01} = atan(\frac{3}{1})= 1,249 = 71,6°$
$\alpha_{02} = atan(\frac{4}{3})= 0,927 = 53,1°$
$\alpha_{03} = atan(\frac{0}{3})= 0= 0°$
Dann ergeben sich die zerlegten Kräfte zu:
\begin{align*} F_{x,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{x,0n} = F_{0n} \cdot sin(\alpha_{0n}) \\ F_{x,0} &= (-5N) \cdot sin(71,6°) + (-6N) \cdot sin(53,1°) + (+3N) \cdot sin(0°) \\ F_{x,0} &= -2,18 N \\ \\ F_{y,0} &= F_{x,01} + F_{x,02} + F_{x,03} && | \quad \text{mit } F_{y,0n} = F_{0n} \cdot cos(\alpha_{0n}) \\ F_{y,0} &= (-5N) \cdot cos(71,6°) + (-6N) \cdot cos(53,1°) + (+3N) \cdot cos(0°) \\ F_{y,0} &= -9,54 N \\ \\ \end{align*}
Exercise 2.7.7 Simplifying Circuits (exam task, about 8% of a 60-minute exam, WS2020)
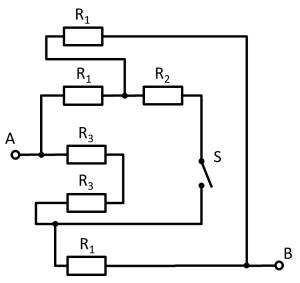
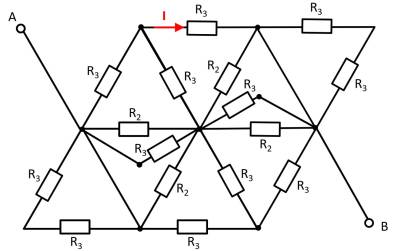
Given is the adjoining circuit with
$R_1=10 ~\Omega$
$R_2=20 ~\Omega$
$R_3=5 ~\Omega$
and the switch $S$.
1. Determine the total resistance $R_{\rm eq}$ between A and B by summing the resistances with the switch $S$ open.
- How can the circuit be better represented or pulled apart?
- The switch should be replaced by an open wire in this case.
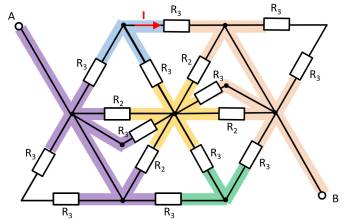
For this purpose, the individual branches can be highlighted in color and interpreted as a “conductive rubber band”.
This results in:
Thus $R_3$ and $R_3$ can be combined to $R_{33} = 2 \cdot R_3 = R_1$, yielding a left and a right voltage divider.
Now it is visible that in the left and right voltage divider, the same potential is at the respective branch, or at the node K1 (green) and K2 (pink).
Thus, the total resistance can be calculated as $R_{\rm eq} = (2 \cdot R_1)||(2 \cdot R_1)$.
However, by symmetry, nodes K1 and K2 can also be short-circuited. Thus, $R_{\rm eq} = 2 \cdot \left( R_1||R_1 \right)$ also holds.
2. What is the total resistance when switch $S$ is closed?
So the resistance remains the same.
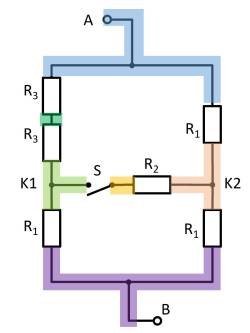
Exercise 2.7.8: Simplifying Circuits II (written exam task, approx 8% of a 60-minute written exam, WS2020)
Given is the adjoining circuit with
$R_1=5 ~\Omega$
$R_2=10 ~\Omega$
$R_3=20 ~\Omega$
1. Determine the equivalent resistance $R_{\rm eq}$ between A and B by summing the resistances.
- How can the circuit be better represented or pulled apart?
- Switches (when used) should be replaced by an open or closed circuit.
- Does this result in equal potentials at different nodes that can be cleverly used?
For this purpose, the individual branches can be highlighted in color and interpreted as a “conductive rubber band”.
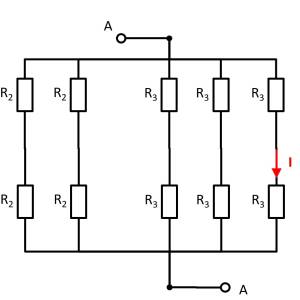
It can be seen that the two resistors $R_3$ at the top left and bottom right are each shorted. The result is thus:
Here it helps to consider the potential of the nodes K1, K2, and K3. For K2, the resistances $R_2 || R_3 || R_2$ must be combined at the top and bottom. Thus, the same resistance values at the top and bottom result. Also at the nodes K1 and K2 the same resistance values at the top and at the bottom result. With the same ratios of the resistances at K1, K2, and K3 respectively, it can be concluded that no current flows across the resistors $R_3$ between K1 and K2 or K2 and K3. Thus, these do not contribute to the total resistance. In such a case, a short circuit or an open line can be freely chosen between the relevant nodes for the calculation. In the following, an open line is chosen. Additionally, the parallel strings can be reordered.
This results in:
\begin{align*} R_{\rm eq} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) && || \; \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{\rm eq} &= R_2 && || \;\frac{2}{3}\cdot R_3 \\ R_{\rm eq} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} \\ R_{\rm eq} &= \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Now let the voltage from A to B be: $U_{AB}=U_0= 20 ~\rm V$. What is the current $I$?
Aufgabe 4.5.2: open circuit voltage via superposition (exam task, approx. 12 % of a 60-minute exam, WS2020)
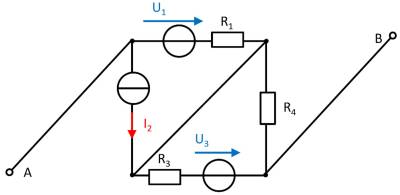
A circuit is given with the following parameters
$R_1=5 ~\Omega$
$U_1=2 ~\rm V$
$I_2=1 ~\rm A$
$R_3=20 ~\Omega$
$U_3=8 ~\rm V$
$R_4=10 ~\Omega$
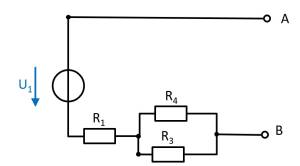
Determine the open circuit voltage between A and B using the principle of superposition.
- What do the individual circuits look like, by which the effects of the individual sources can be calculated?
Which equivalent resistor must be used to replace a current or voltage source when calculating the individual effects? - Where are the open-circuit voltages applied when looking at the individual components?
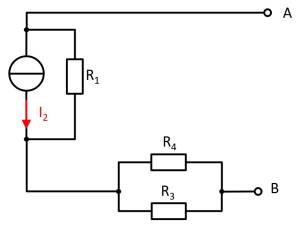
(Voltage) source $U_1$
- substitute the current source $I_2$ with a short-circuit
- substitute the voltage source $U_3$ with an open circuit
The components can be moved in order to understand the circuit s bit better.
For the open circuit, no current is flowing through any resistor. Therefore, the effect is: $U_{AB,1} = U_1$
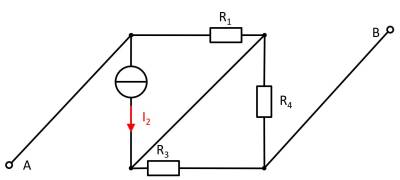
(current) source $I_2$
- substitute the voltage source $U_1$ with an open circuit
- substitute the voltage source $U_3$ with an open circuit
Also here, the components can be shifted for a better understanding:
Here, the current source $I_2$ creates a voltage drop $U_{AB_2}$ on the resistor $R_2$ : $U_{\rm AB,2} = - R_1 \cdot I_2$
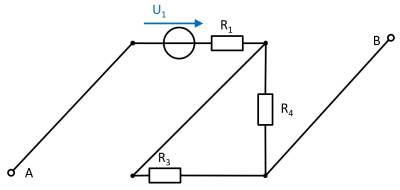
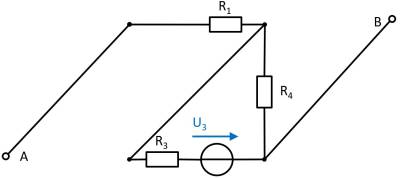
(Voltage) source $U_3$
- substitute the voltage source $U_1$ with an open circuit
- substitute the current source $I_2$ with a short-circuit
Again, rearranging the circuit might help for an understanding:
In this case, between the unloaded outputs $\rm A$ and $\rm B$ there will be an unloaded voltage divider given by $R_3$ and $R_4$.
On $R_1$ there is no voltage drop since there is no current flow out of the unloaded outputs.
Therefore:
\begin{align*} U_{\rm AB,3} = \frac{R_4}{R_3 + R_4} \cdot U_3 \end{align*}
resulting voltage
\begin{align*} U_{\rm AB} &= U_1 - R_1 \cdot I_2 + \frac{R_4}{R_3 + R_4} \cdot U_3 \\ \end{align*}
Aufgabe 3.1.3: Last an linearer Quelle (Klausuraufgabe, ca 8% einer 60minütigen Klausur, WS2020)
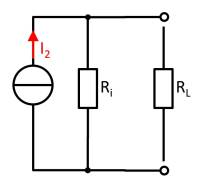
Gegeben ist eine lineare Stromquelle, welche eine ohmsche Last $R_L=10\Omega$ versorgt. Es ergibt sich ein Strom an der Last von $I_L=2A$. Der Kurzschlussstrom ist $5 A$.
1. Zeichnen Sie das Ersatzschaltbild des Aufbaus.
- Wie Sieht eine lineare Stromquelle aus?
- Wie wird die Last verschalten?
2. Wie groß die der Innenleitwert der Quelle?
- Im Kurzschlussfall fließt der Kurzschlussstrom nur durch $R_L$
- Für eine Vereinfachung der Rechnung bietet es sich an die lineare Stromquelle in eine lineare Spannungsquelle umzuwandeln.
Die Umwandlung wandelt auch die Schaltung von einer Parallelschaltung in eine Reihenschaltung.
Die Spannung $U_{LL}$ liegt also am Spannungsteiler aus $R_i$ und $R_L$: $U_{LL} = U_i + U_L$
Mit dem Lastwiderstand $R_L$ ergibt sich ein Strom von $I_L$ durch die Reihenschaltung.
Mit den gegebenen $R_L$ und $I_L$ lässt sich die Spannung $U_L$ an der Last berechnen.
Die restliche Spannung $U_i$ liegt am Innenwiderstand $R_i$ an, durch den auch der Strom $I_L$ fließt. Somit ergibt sich für den Leitwert $G_i$:
\begin{align*} U_{LL} &= U_i + U_L \\ R_i \cdot I_{KS} &= R_i \cdot I_L + R_L \cdot I_L \\ R_i \cdot I_{KS} - R_i \cdot I_L &= R_L \cdot I_L \\ R_i \cdot (I_{KS} - I_L) &= R_L \cdot I_L \\ R_i &= R_L \cdot \frac{I_L}{I_{KS} - I_L} \\ G_i &= \frac{I_{KS} - I_L}{R_L \cdot I_L} \\ \end{align*}
3. Welche Leistung nimmt die Last auf?
Exercise 1.6.6: Temperature-dependent resistance of a winding (written test, approx. 6 % of a 60-minute written test, WS2020)
On the rotor of an asynchronous motor, the windings are designed in copper.
The length of the winding wire is $40~\rm{m}$.
The diameter is $0.4~\rm{mm}$.
When the motor is started, it is uniformly cooled down to the ambient temperature of $20~°\rm{C}$.
During operation the windings on the rotor have a temperature of $90~°\rm{C}$.
$\alpha_{Cu,20~°\rm{C}}=0.0039 ~\frac{1}{\rm{K}}$
$ \beta_{Cu,20~°\rm{C}}=0.6 \cdot 10^{-6} ~\frac{1}{\rm{K}^2}$
$ \rho_{Cu,20~°\rm{C}}=0.0178 ~\frac{\Omega \rm{mm}^2}{\rm{m}}$
Use both the linear and quadratic temperature coefficients! 1. determine the resistance of the wire for $T = 20~°\rm{C}$.
2. what is the increase in resistance $\Delta R$ between $20~\rm °C$ and $90~\rm °C$ for one winding?
Aufgabe 5.9.3: temperaturabhängiger Widerstand einer Wicklung (Klausuraufgabe, ca 6% einer 60minütigen Klausur, WS2020)
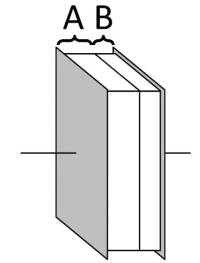
Bestimmen Sie die Kapazität $C$ für den rechts gezeichneten Plattenkondensator mit den folgenden Daten:
- rechteckige Elektroden mit einer Kantenlänge von $6 cm$ und $8 cm$
- Abstand der Platten: $2 mm$
- Dielektrikum A:
- $\varepsilon_{r,A} = 1 (Luft)$
- Dicke $d_A = 1,5 mm$
- Dielektrikum B:
- $\varepsilon_{r,B} = 100 (Eis)$
- Dicke $d_B = 0,5 mm$
$\varepsilon_{0} = 8,854 \cdot 10^{-12} F/m$
- Durch welche Schaltung lässt sich ein geschichteter Aufbau mit unterschiedlichen Dielektrika ersetzen?
Es ergibt sich somit: $C = \frac{C_A \cdot C_B}{C_A + C_B}$
Die Teilkapazität $C_A$ lässt sich berechnen durch \begin{align*} C_A &= \varepsilon_{0} \varepsilon_{r,A} \cdot \frac{A}{d_A} && | \text{mit } A = 3 cm \cdot 5cm = 6 \cdot 10^{-2} \cdot 8 \cdot 10^{-2} m^2 = 48 \cdot 10^{-4} m^2\\ C_A &= 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{1,5 \cdot 10^{-3} m} \\ C_A &= 28,33 \cdot 10^{-12} F \\ \end{align*}
Die Teilkapazität $C_B$ lässt sich berechnen durch \begin{align*} C_B &= \varepsilon_{0} \varepsilon_{r,B} \cdot \frac{B}{d_B} \\ C_B &= 100 \cdot 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{0,5 \cdot 10^{-3} m} \\ C_B &= 8,500 \cdot 10^{-9} F \\ \end{align*}
Exercise 5.2.3: Charging and Discharging of RC elements (exam task, ca. 11 % of a 60-minute exam, WS2020)
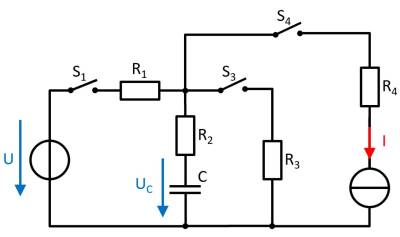
The circuit shown right is given with the following data:
- $U = 10 ~{\rm V}$
- $I = 4 ~{\rm mA}$
- $R_1 = 100 ~\Omega, R_2 = 80 ~\Omega, R_3 = 50 ~\Omega, R_4 = 10 ~\Omega$
- $C = 40 ~{\rm nF}$
At first, the voltage drop on the capacitor $u_C = 0$, and all switches are open. The switch S1 will be closed at $t = 0$.
1. Determine the time constant $\tau$ for this charging process.
- What equivalent circuit can be found for the mentioned states of the switches?
- What parameter do you need to determine $\tau$?
- The charging current is flown through which component?
2. What is the value of the voltage $u_C(t)$ drop over the capacitor $C$ at $t=10 ~{\rm µs}$?
3. What is the value of the stored energy in the capacitor, when it is fully charged?
4. Determine the new time constant when the switch $S_1$ will be opened and the switch $S_3$ will be closed simultaneously.
5. When the capacitor is completely discharged, all switches will be opened. The switch $S_4$ will be closed at $t= 0$.
What is the voltage $u_C$ at the capacitor C after $t = 1 ~ {\rm µs}$?
- Through the current source there is a continuous flow of electric charge into the capacitor.
- The resistors passed by the current on the way to the capacitor are irrelevant. They only increase the voltage of an ideal current source to guarantee the current.