Aufgabe 5.9.3: temperaturabhängiger Widerstand einer Wicklung (Klausuraufgabe, ca 6% einer 60minütigen Klausur, WS2020)
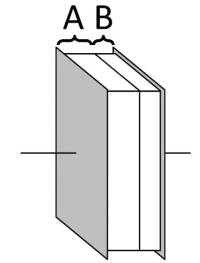
Bestimmen Sie die Kapazität $C$ für den rechts gezeichneten Plattenkondensator mit den folgenden Daten:
- rechteckige Elektroden mit einer Kantenlänge von $6 cm$ und $8 cm$
- Abstand der Platten: $2 mm$
- Dielektrikum A:
- $\varepsilon_{r,A} = 1 (Luft)$
- Dicke $d_A = 1,5 mm$
- Dielektrikum B:
- $\varepsilon_{r,B} = 100 (Eis)$
- Dicke $d_B = 0,5 mm$
$\varepsilon_{0} = 8,854 \cdot 10^{-12} F/m$
- Durch welche Schaltung lässt sich ein geschichteter Aufbau mit unterschiedlichen Dielektrika ersetzen?
Es ergibt sich somit: $C = \frac{C_A \cdot C_B}{C_A + C_B}$
Die Teilkapazität $C_A$ lässt sich berechnen durch \begin{align*} C_A &= \varepsilon_{0} \varepsilon_{r,A} \cdot \frac{A}{d_A} && | \text{mit } A = 3 cm \cdot 5cm = 6 \cdot 10^{-2} \cdot 8 \cdot 10^{-2} m^2 = 48 \cdot 10^{-4} m^2\\ C_A &= 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{1,5 \cdot 10^{-3} m} \\ C_A &= 28,33 \cdot 10^{-12} F \\ \end{align*}
Die Teilkapazität $C_B$ lässt sich berechnen durch \begin{align*} C_B &= \varepsilon_{0} \varepsilon_{r,B} \cdot \frac{B}{d_B} \\ C_B &= 100 \cdot 8,854 \cdot 10^{-12} F/m \cdot \frac{48 \cdot 10^{-4} m^2}{0,5 \cdot 10^{-3} m} \\ C_B &= 8,500 \cdot 10^{-9} F \\ \end{align*}