Dies ist eine alte Version des Dokuments!
2. Simple DC circuits
So far, only simple circuits consisting of a source and a load connected by wires have been considered.
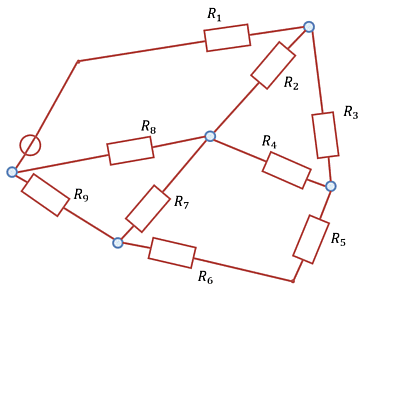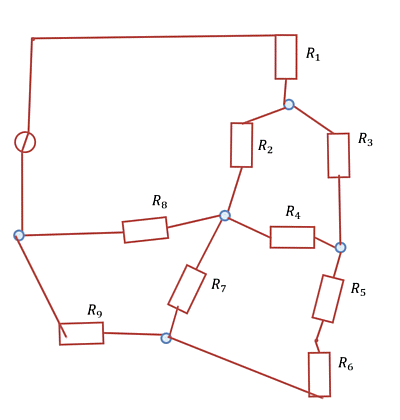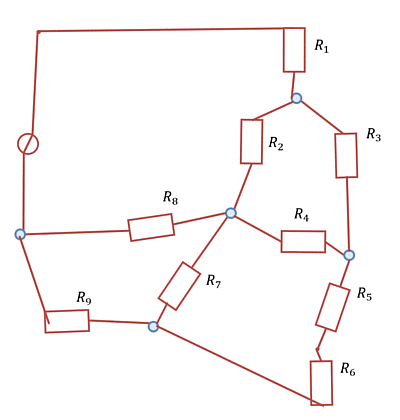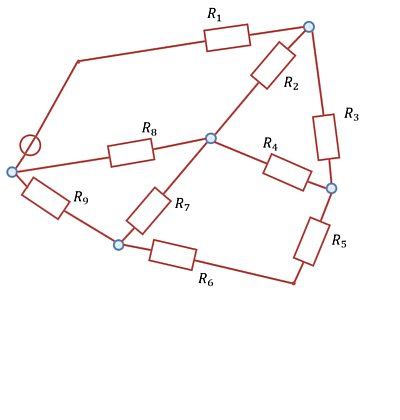
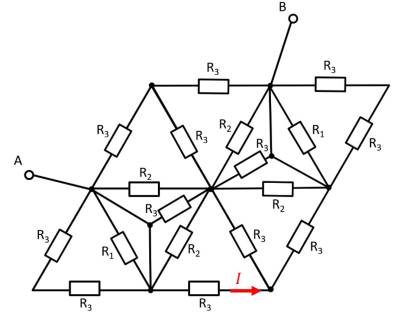
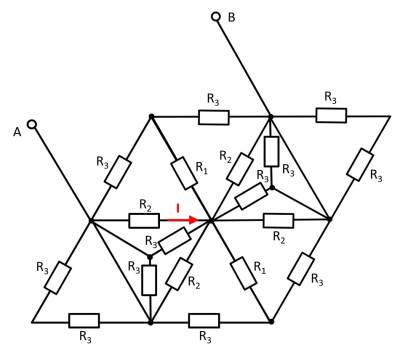
In the following, more complicated circuit arrangements will be analysed. These initially contain only one source, but several lines and many ohmic loads (cf. Abbildung 1).
2.1 ideal components
goals
After this lesson you should:
- Know the representation of ideal current and voltage sources in the U-I diagram.
- Know the internal resistance of ideal current and voltage sources.
- Know the symbol of ideal current and voltage sources.
- Know the properties of ideal resistance and ideal connection.
Every electrical circuit consists of three elements:
- Consumers: consumers convert electrical energy into energy that is not purely electrical.
e.g.- into electrostatic energy (capacitor)
- into magnetostatic energy (magnet)
- into electromagnetic energy (LED, light bulb)
- into mechanical energy (loudspeaker, motor)
- into chemical energy (charging an accumulator)
- sources (generators): sources convert energy from another form of energy into electrical energy. (e.g. generator, battery, photovoltaic).
- wires (interconnections): the wires of interconnection lines link consumers to sources.
These elements will be considered in more detail below.
Consumer
- The colloquial term 'consumer' in electrical engineering stands for an electrical consumer - i.e. a component which converts electrical energy into another form of energy.
- A resistor is often also referred to as a consumer. In addition to pure ohmic consumers, however, there are also ohmic-inductive consumers (e.g. coils in a motor) or ohmic-capacitive consumers (e.g. various power supplies using capacitors at the output). Correspondingly the equation „consumer is a resistor“ is wrong.
- Current-voltage characteristics (vgl. Abbildung 2)
- Current-voltage characteristics of a load always run through the origin, because without current there is no voltage and vice versa.
- Ohmic loads have a linear current-voltage characteristic which can be described by a single numerical value.
The slope in the $U$-$I$-characteristic is the conductance: $I = G \cdot U = {{U}\over{R}}$
Sources
- Sources act as generators of electrical energy
- A distinction is made between ideal and real sources.
The real sources are described in the following chapter (non-ideal_sources_and_two_pole_networks).
The ideal voltage source generates a defined constant output voltage $U_s$ (in German often $U_q$ for Quellenspannung).
In order to maintain this voltage, it can supply any current.
The current-voltage characteristic also represents this (see Abbildung 3).
The circuit symbol shows a circle with two terminals. In the circuit, the two terminals are short-circuited.
Another circuit symbol shows the negative terminal of the voltage source as a „thick minus symbol“, the positive terminal is drawn wider.
The ideal current source produces a defined constant output current $I_s$ (in German often $I_q$ for Quellenstrom).
For this current to flow, any voltage can be applied to its terminals.
The current-voltage characteristic also represents this (see Abbildung 4).
The circuit symbol shows again a circle with two connections. This time the two connections are left open in the circle and a line is drawn perpendicular to them.
wire connection
- The ideal connection line is resistance-free and transmits current and voltage instantaneously.
- Real existing influences (e.g. voltage drop) of connections are considered via separately drawn components (e.g. ohmic resistance).
2.2 Reference-arrow Systems and first consideration of a DC circuit
Goals
After this lesson you should:
- Be able to apply and distinguish between the producer and consumer reference arrow systems.
In the chapter 1. Preparation and Proportions the conventional directional sense of currents and voltages has already been discussed. Unfortunately, with meshed networks it is often not clear ahead of the calculation in which direction the conventional sense of direction of all currents and voltages runs.
In Abbildung 5 such a meshed net is shown. In this circuit a switch $S_1$ and a current $I_2$ are marked. Once the state of the switch is swapped, the direction of the current changes.
Generator and Load (Reference) Arrow System
For the direction of the arrows different conventions are available. Here (and quite often in Germany) the convention of power engineering is used. This convention is
Generator Reference Arrow System
With sources (or generators), energy is taken from the environment and made available to the circuit.
For generators, the arrowfoot of the current is attached to the arrowhead of the voltage. Voltage and current arrows are antiparallel ($\uparrow \downarrow$).
For generators holds: $P_{1} = U_{12} \cdot I_1 \stackrel{!}{>} 0$
The power transfer from the environment to the power system via the generator or the generator arrow system is calculated positively.
Load Reference Arrow System
In the case of consumers, energy is taken from the circuit and made available to the environment.
For consumers, the arrowfoot or arrowhead of the current and voltage are related. Voltage and current arrows are parallel ($\uparrow \uparrow$).
For consumers, the following holds:
$P_{3} = U_{34} \cdot I_3 \stackrel{!}{>} 0$
The power transfer from the power system to the environment via the consumer or the consumer arrow system is also calculated positively.
Note:
- Before the calculation, the reference arrows for currents and voltages are set arbitrarily, with the following conditions:
- the generator arrow system - current antiparallel to the voltage arrow - is used for all sources (e.g. all voltage and current sources)
- the motor arrow system - current parallel to the voltage arrow - is used for all consumers (e.g. all passives like resistors, capacitors, inductors, diodes etc.)
- for loads, where the direction of the power is not known, the motor arrow system is recommented (e.g. passives, in case what these are part of a machine, like inductors of a motor)
- After the calculation means
- $I>0$: The reference arrow reflects the conventional directional sense of the current
- $I<0$: The reference arrow points in the opposite direction to the conventional directional sense of the current
- Reference arrows of the current are drawn in the wire if possible.
The reference arrow system
2.3 Nodes, Branches and Loops
Explanation of the different network structures
(Graphs and trees are only needed in later chapters)
Goals
After this lesson you should:
- Be able to identify the nodes, branches and loops in a circuit.
- Be able to use them to make a circuit clearer.
Electrical circuits typically have the structure of networks. Networks consist of two elementary structural elements:
- Branches (German: Zweige): Connections between two nodes
- Node (German: Knoten): Connection points of several branches
Please note in the case of electrical circuits:
- Branches contain at least one component.
- Nodes connect more than two branches and can also be spatially extended.
Branches in electrical networks are also called two-pole. Their behaviour is described by current-voltage characteristics and explained in more detail in the chapter non-ideal_sources_and_two_pole_networks .
In addition, another term is to be explained:
A loop is a closed path in the mesh. This means that a loop begins and ends at the same node and runs over at least one further node.
Since a voltmeter can also be present as a component between two nodes, it is also possible to close a loop by a drawn voltage arrow (cf. $U_1$ in Abbildung 10).
Please keep in mind, that usually the entire behaviour of networked circuits almost always changes when a change occurs in one branch or at one node. This is in contrast to other cause-effect relationships, but comparable to changes in other larger networks, e.g. a traffic jam in the road network, due to which other roads experience a higher load. For electrical engineering, this means that in the case of changing circuits, the focus is often on determining the interrelationships (formulas, current-voltage characteristics) and not on a single numerical value.
Simplifications
With the knowledge of nodes, branches and meshes, circuits can be simplified. Circuits can be reshaped arbitrarily as long as all branches remain at the same nodes after reshaping The Abbildung 11 shows how such a transformation is possible.
For practical tasks, repeated trial and error can be useful. It is important to check afterwards that the same components are connected to each node as before the transformation.
Further examples can be found in the following video
Exercise 2.3.1 Branches and Nodes
For the markings in the circuits in Abbildung 12 indicate whether it is a branch, a node, or neither.
Exercise 2.3.2 Simplifications of circuits
Simplify the circuits in Abbildung 13.
2.4 Kirchhoff's circuit laws
Representation and application of Kirchhoff's circuit laws
Goals
After this lesson you should: Know and be able to apply Kirchhof's circuit laws (Kirchhoff's current law andKirchhoff's voltage law).
Kirchhoff's current law (Kirchhoff's first law)
The Kirchhoff's current law (Kirchhoff's nodal rule, in German: Knotensatz) formulates in the language of mathematics the experience that no charge „accumulations“ occur in electrical wires. This is of particular relevance at a network node (Abbildung 14). To formulate the equation at this node, the reference arrows of the currents are all set in the same way. That means: all point away from or towards the node.
Note:
The sum of all currents flowing from the nodes must be zero.
$\boxed{I_1 + I_2 + I_3 + ... + I_n = \sum_{x=1}^{n} I_x=0}$
From now on, the following definition applies:
- Currents whose current arrows point towards the node are added in the calculation.
- Currents whose current arrows point away from the node are subtracted in the calculation.
Parallel circuit of resistors
From the Kirchhoff's current law, the total resistance for resistors connected in parallel can be derived (Abbildung 15):
Since the same voltage $U_{ab}$ is dropped across all resistors, using the Kirchhoff's current law:
$\large{{U_{ab}}\over{R_1}}+ {{U_{ab}}\over{R_2}}+ ... + {{U_{ab}}\over{R_n}}= {{U_{ab}}\over{R_{substitute}}$
$\rightarrow \large{{{1}\over{R_1}}+ {{1}\over{R_2}}+ ... + {{1}\over{R_n}}= {{1}\over{R_{substitute}} = \sum_{x=1}^{n} {{1}\over{R_x}}$
Thus, for resistors connected in parallel, the equivalent conductance $G_{eq}$ (German: Ersatzleitwert) is the sum of the individual conductances: $G_{eq} = \sum_{x=1}^{n} {G_x}$
In general: the equivalent resistance of a parallel circuit is always smaller than the smallest resistance.
Especially for two parallel resistors $R_1$ and $R_2$ applies: $R_{eq}= \large{{R_1 \cdot R_2}\over{R_1 + R_2}}$
Current divider
Derivation of the current divider with further considerations
The current divider rule can also be derived from the Kirchhoff's current law.
This states that, for resistors $R_1, ... R_n$ their currents $I_1, ... I_n$ behave just like the conductances $G_1, ... G_n$ through which they flow.
$\large{{I_1}\over{I_g}} = {{G_1}\over{G_g}}$
$\large{{I_1}\over{I_2}} = {{G_1}\over{G_2}}$
Exercise 2.4.1 Current divider
In the simulation in Abbildung 16 a current divider can be seen. The resistances are just inversely proportional to the currents flowing through it.
- What currents would you expect in each branch if the input voltage were lowered from $5V$ to $3.3V$? After thinking about your result, you can adjust the
Voltage(bottom right of the simulation) accordingly by moving the slider. - Think about what would happen if you flipped the switch before you flipped the switch.
After you flip the switch, how can you explain the current in the branch?
Exercise 2.4.2 two resistors
Two resistors of $18\Omega$ and $2 \Omega$ are connected in parallel. The total current of the resistors is $3A$.
Calculate the total resistance and how the currents is split to the branches.
Kirchhoff's voltage law (Kirchhoff's second law)
Also the Kirchhoff's voltage law describes in mathematical language another practical experience: Between two points $1$ and $2$ of a network there is only one potential difference. Thus the potential difference is in particular independent of the way a network is traversed between the two points $1$ and $2$. This can be described by considering the meshes.
Note:
In any mesh of an electrical circuit, the sum of all voltages is always zero (Abbildung 17):
$\boxed{U_{1} + U_{2} + ... + U_{n} = \sum_{x=1}^{n} U_x = 0}$
To calculate this, a convention for the loop direction must be specified. Theoretically this can be chosen arbitrarily. In practice, often a specific direction (e.g. clockwise) is used.
Independently, the following specification always applies: For voltage drop the inverse sign of a voltage risde has to be taken into account.
For example:
- Voltages, whose voltage arrows point in the direction of circulation are added in the calculation.
- Voltages, whose voltage arrows point against the direction of rotation are subtracted in the calculation.
Proof of Kirchhoff's voltage law
If one expresses the voltage in Abbildung 17 dby the potentials in the nodes, we get:
$U_{12}= \varphi_1 - \varphi_2 $
$U_{23}= \varphi_2 - \varphi_3 $
$U_{34}= \varphi_3 - \varphi_4 $
$U_{41}= \varphi_4 - \varphi_1 $
If these voltages are added, this leads to Kirchhoff's voltage law.
$U_{12}+U_{23}+U_{34}+U_{41} = 0$
Series circuit of resistors
Using Kirchhoff's voltage law, the total resistance of a series circuit (in German: Reihenschaltung, see <imref FigNo13>) can be easily determined:
$U_1 + U_2 + ... + U_n = U_g$
$R_1 \cdot I_1 + R_2 \cdot I_2 + ... + R_n \cdot I_n = R_{ersatz} \cdot I $
Since in series ciruit the current through all resistors must be the same - i.e. $I_1 = I_2 = ... = I$ - it follows that:
$R_1 + R_2 + ... + R_n = R_{eq} = \sum_{x=1}^{n} R_x $
In general: The equivalent resistance of a series circuit is always greater than the greatest resistance..
Exercise 2.4.3 Three Resistors
Three equal resistors of $20k\Omega$ each are given.
Which values are realizable by arbitrary interconnection of one to three resistors?
2.5 Unloaded and loaded voltage divider
The unloaded voltage divider
Derivation of the unloaded voltage divider
Goals
After this lesson you should be able to:
- to distinguish between the loaded and unloaded voltage divider.
- to describe the differences between loaded and unloaded voltage dividers.
Especially the series ciruit of two resistors $R_1$ and $R_2$ shall be considered now. This situation occurs in many practical applications (e.g. potentiometer). In Abbildung 21 this circuit is shown.
Via the Kirchhoff's voltage law we get
$\boxed{ {{U_1}\over{U}} = {{R_1}\over{R_1 + R_2}} }$
The ratio $k={{R_1}\over{R_1 + R_2}}$ also corresponds to the position on a potentiometer.
Exercise 2.5.1 unbelasteter Spannungsteiler
In the simulation in Abbildung 22 an unloaded voltage divider in the form of a potentiometer can be seen. The ideal voltage source provides $5V$. The potentiometer has a total resistance of $1K\Omega$. In the configuration shown, this is divided out to $500 \Omega$ and $500 \Omega$.
- What voltage $U_out$ would you expect if the switch were closed? After thinking about your result, you can check it by closing the switch.
- First think about what would happen if you would change the distribution of the resistors by moving the wiper („intermediate terminal“)?
You can check your assumption by using the slider at the bottom right of the simulation. - At which position do you get a $U_out = 3.5V$?
The loaded voltage divider
If - in contrast to the above-mendtioned, unloaded voltage divider - a load $R_L$ is connected to the output terminals (Abbildung 23), this load influences the output voltage.
A circuit analysis yields:
$ U_1 = \LARGE{{U} \over {1 + {{R_2}\over{R_L}} + {{R_2}\over{R_1}} }} }$
or on a potentiometer with $k$ and the sum of resistors $R_s = R_1 + R_2$:
$ U_1 = \LARGE{{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}} }} }$
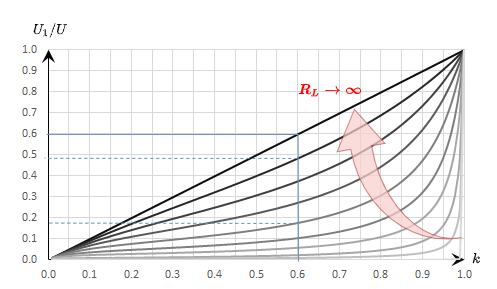
Abbildung 24 shows the ratio of the output voltage $U_1$ to the input voltage $U$ (y-axis), in relation to the ratio $k={{R_1}\over{R_1 + R_2}}$. In principle, this is similar to Abbildung 21, but here it has another dimension: multiple graphs are plotted. These differ by the ratio ${{R_s}\over{R_L}}$.
What does this diagram tell us? This shall be investigated by an example. First, assume an unloaded voltage divider with $R_2 = 4 k\Omega$ and $R_1 = 6 k\Omega$, and an input voltage of $10V$. Thus $k = 0.6$, $R_s = 10k\Omega$ and $U_1 = 6V$. Now this voltage divider is loaded with a load resistor. If this is at $R_L = R_1 = 10 k\Omega$, $k$ reduces to about $0.48$ and $U_1$ reduces to $4.8V$ - so the output voltage drops. For $R_L = 4k\Omega$, $k$ becomes even smaller to $k=0.375$ and $U_1 = 3.75V$. If the load $R_L$ is only one tenth of the resistor $R_s=R_1 + R_2$, the result is $k=0.18$ and $U_1=1.8V$. The output voltage of the unloaded voltage divider ($6V$) thus became less than one third.
What is the practical use of the (loaded) voltage divider?
Here some examples:
- Voltage dividers are in use for controlling the output of power supply IC's (see Voltage Dividers in Power Supplies). In order not to create a loaded voltage divider, a range for the resistance is given here.
- Another „invisible“ voltage divider is for example in the electical system of a car. As we will learn in the next chapters, voltage supplies have in internal resistance (and therefore batteries, too). The other consumer in the car also represent a resistance. By this, the electical system states an unloaded voltage divider. Given another, additional low-resistance load (e.g. the spark of the starter system) one can understand that there will be a voltage drop when starting the car.
Exercise 2.5.2 loaded voltage divider I
Determine from the circuit in Abbildung 23 the above equation $ U_1 = {{k \cdot U} \over { 1 + k \cdot (1-k) \cdot{{R_s}\over{R_L}}}}$ where $k={{R_1}\over{R_1 + R_2}}$ and $R_s = R_1 + R_2$.
Exercise 2.5.3 loaded voltage divider II
In the simulation in Abbildung 25 a loaded voltage divider in the form of a potentiometer can be seen. The ideal voltage source provides $5V$. The potentiometer has a total resistance of $1K\Omega$. In the configuration shown, this is divided out to $500 \Omega$ and $500 \Omega$. The load resistance has $R_L = 1 k\Omega$.
- What voltage
U_OUTwould you expect if the switch were closed? This is where you need to do some math! After you calculated your result, you can check it by closing the switch. - At which division you get $3.5V$. Determine the result first for a calculation.
Then check it by moving the slider at the bottom right of the simulation.
Exercise 2.5.4 Application of the loaded voltage divider - motor
You wanted to test a micromotor for a small robot. Using the maximum current and the internal resistance ($R_M = 5\Omega$) you calculate that this can be operated with a maximum of $U_{M,max}=4V$. A colleague said that you can get $4V$ using the setup in Abbildung 26 from a $9V$ block battery.
- First, calculate the maximum current $I_{M,max}$ of the motor.
- Draw the corresponding electrical circuit with the motor connected as an ohmic resistor.
- At the maximum current, the motor should be able to deliver a torque of $M= 100mNm$. What torque would the motor deliver if you implement the setup like this? (Assumption: The torque of the motor increases proportionally to the motor current).
- What might a setup with a potentiometer look like that would actually allow you to set a voltage between $0.5V$ to $4V$ on the motor? What resistance value should the potentiometer have?
- Build and test your circuit in the simulation below. For an introduction to online simulation, see: online_circuit_simulator.
You will essentially need the following tips for this setup:- Routing connections can be activated via the menu:
Draw»add wire. Afterwards you have to click on the start point and then drag to the end mode. - Note that connections can only ever be connected at nodes. A red marked node (e.g. at the $5 \Omega$ resistor) indicates that it is not connected. This could be moved one grid step to the left, as there is a node point there.
- Pressing the
<ESC>key will disable the insertion of components. - With a right click on a component it can be copied or values like the resistor can be changed via
Edit….
Exercise 2.5.5 Examples of the calculation of loaded voltage dividers
Voltage divider, series circuit (series resistance) and shunt resistor
Exercise on the voltage divider
Exercise 2.5.6 Example of a loaded voltage divider: Explanation without calculation
2.6 Star-delta circuit
Goals
After this lesson you should:
- be able to convert triangular loops into a star shape (and vice versa)
At the beginning of the chapter an example of a network was shown (Abbildung 1). Here, however, one does not come directly to the solution with the set of nodes and loops. It is visible, that there are many triangle-shaped loops resp. star-shaped nodes (Abbildung 28). These will be discussed in more detail now.
First of all a summary of the previous findings. Using the node and loop rule it became clear that an equivalent resistance can be determined from a series as well as from a parallel circuit. If one considers the equivalent resistance as a black box - i.e. the internals are unknown - it could be interpreted by both types of circuit (Abbildung 29).
Now how does this help us in the case of a triangular loop?
Also in this case one can provide a black box. However, this should always behave in the same way as the triangular loop, i.e. any voltages applied should produce the same currents as the known structure.
In other words: The resistances measured between two terminals must be identical for the blackbox and the known circuit.
For this purpose, the different resistances between the individual nodes $a$, $b$ and $c$ are now to be considered, see Abbildung 30. The aim is to find out how a delta circuit can be developed from a star circuit (and vice versa).
Abb. 30: Star-delta transformation
Calculation of the transformation formulae: Star connection in delta connection
Delta circuit
In the delta connection, the 3 resistors $R_{ab}^1$, $R_{bc}^1$ and $R_{ca}^1$ are connected in a loop this terminals on each node.
For the resistors between the two terminals (e.g. $a$ and $b$), the third one ($c$) is considered as not connected to anything outside. This results in a parallel circuit of the direct star resistor $R_{ab}^1$ with the series connection of the other two star resistors $R_{ca}^1 + R_{bc}^1$:
$R_{ab} = R_{ab}^1 || (R_{ca}^1 + R_{bc}^1) $
$R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + (R_{ca}^1 + R_{bc}^1)}} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} $
The same applies to the other connections. This results in:
\begin{align*} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \tag{2.6.1} \end{align*}
Star circuit
Given the idea, that the star ciruict shall behave equal to the delta circuit, the resistance measured between the terminals must be similar. Also in the star connection 3 resistors are connected, but in a star shape. The star resistors are all connected with another node $0$ in the middle: $R_{a0}^1$, $R_{b0}^1$ and $R_{c0}^1$.
Again, the procedure is the same as for the delta connection: the resistance between two terminals (e.g. $a$ and $b$) is determined, and the further terminal ($c$) is considered open. The resistance of the further terminal ($R_{c0}^1$) is only connected at one node. Therefore, no current flows through it - it is thus not to be considered. It results in:
\begin{align*} R_{ab} = R_{a0}^1 + R_{b0}^1 \\ R_{bc} = R_{b0}^1 + R_{c0}^1 \\ R_{ca} = R_{c0}^1 + R_{a0}^1 \tag{2.6.2} \end{align*}
From equations $(2.6.1)$ and $(2.6.2)$ we get:
\begin{align} R_{ab} = {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{a0}^1 + R_{b0}^1 \tag{2.6.3} \end{align} \begin{align} R_{bc} = {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{b0}^1 + R_{c0}^1 \tag{2.6.4} \end{align} \begin{align} R_{ca} = {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} = R_{c0}^1 + R_{a0}^1 \tag{2.6.5} \end{align}
Die Gleichungen $(2.6.3)$ bis $(2.6.5)$ lassen sich nun so geschickt zusammenfassen, dass auf einer Seite nur noch ein Widerstand steht.
Eine Variante ist die Formeln als ${{1}\over{2}} \cdot \left( (2.6.3) + (2.6.4) - (2.6.5) \right)$ bzw. ${{1}\over{2}} \cdot \left(R_{ab} + R_{bc} - R_{ca}\right)$ zu kombinieren. Damit ergibt sich $R_{b0}^1$
\begin{align*} {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} + {{R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} - {{R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( R_{a0}^1 + R_{b0}^1 + R_{b0}^1 + R_{c0}^1 - R_{c0}^1 - R_{a0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 \cdot (R_{ca}^1 + R_{bc}^1)} + {R_{bc}^1 \cdot (R_{ab}^1 + R_{ca}^1)} - {R_{ca}^1 \cdot (R_{bc}^1 + R_{ab}^1)}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= {{1}\over{2}} \cdot \left( 2 \cdot R_{b0}^1 \right) \\ {{1}\over{2}} \cdot \left( {{R_{ab}^1 R_{ca}^1 + R_{ab}^1 R_{bc}^1 + R_{bc}^1 R_{ab}^1 + R_{bc}^1 R_{ca}^1 - R_{ca}^1 R_{bc}^1 - R_{ca}^1 R_{ab}^1}\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{1}\over{2}} \cdot \left( {{ 2 \cdot R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \right) &= R_{b0}^1 \\ {{ R_{ab}^1 R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} &= R_{b0}^1 \\ \end{align*}
Auf ähnlichem Weg kann man nach $R_{a0}^1$ und $R_{c0}^1$, sowie mit etwas abgewandeltem Ansatz auch auf $R_{ab}^1$, $R_{bc}^1$ und $R_{ca}^1$ auflösen.
Stern-Dreieck-Transformation
Merke:
Soll von einer Dreieckschaltung in eine Sternschaltung umgewandelt werden, so sind die Sternwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{an Anschluss x} \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Produkt der} \\ \text{am Anschluss x liegenden} \\ \text{Dreieckwiderstände} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller} \\ \text{Dreieckwiderstände} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{a0}^1 &= {{ R_{ca}^1 \cdot R_{ab}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{b0}^1 &= {{ R_{ab}^1 \cdot R_{bc}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \\ R_{c0}^1 &= {{ R_{bc}^1 \cdot R_{ca}^1 }\over{R_{ab}^1 + R_{ca}^1 + R_{bc}^1}} \end{align*}
Soll von einer Sternschaltung in eine Dreieckschaltung umgewandelt werden, so sind die Dreieckwiderstände ermittelbar über:
\begin{align*} \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Dreieckwiderstand} \\ \text{zwischen den} \\ \text{Anschlüssen x und y } \end{array} }}} &= {{ \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Summe aller Produkte} \\ \text{zwischen zwei} \\ \text{unterschiedlichen Sternwiderständen} \end{array} }}} } \over { \color{lightgray}{\boxed{ \color{black}{\begin{array}{} \text{Sternwiderstand} \\ \text{gegenüber von x und y} \end{array} }}}}} \\ \\ \text{also:}\quad\quad\quad\quad\quad\quad R_{ab}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{c0}^1}} \\ R_{bc}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{a0}^1}} \\ R_{ca}^1 &= {{ R_{a0}^1 \cdot R_{b0}^1 +R_{b0}^1 \cdot R_{c0}^1 +R_{c0}^1 \cdot R_{a0}^1 }\over{ R_{b0}^1}} \end{align*}
Exercise 2.6.1 Anwendung der Dreieck-Stern-Umwandlung
Exercise 2.6.2 schwierigere Aufgabe mit Stern-Dreieck-Umwandlung
2.7 Gruppenschaltung von Widerständen
Ziele
Nach dieser Lektion sollten Sie:
- Schaltungen, welche nur aus Widerständen bestehen, vereinfachen können.
- die Spannungen und Ströme in Schaltungen mit einer Spannungsquelle und mehreren Widerständen berechnen können.
- symmetrische Schaltungen vereinfachen können.
In diesem Unterkapitel wird auf eine Methodik eingegangen, welche beim Umformen von Schaltungen helfen soll. In Unterkapitel 2.6 Stern-Dreieck-Schaltung wurde gegen Ende bereits ein Netzwerk so umgeformt, dass es keine dreieckigen Maschen mehr enthält. Nun soll dieses Vorgehen systematisiert werden. Ausgangspunkt sind Aufgaben, bei denen für ein Widerstandsnetzwerk der Gesamtwiderstand, Gesamtstrom oder die Gesamtspannung berechnet werden muss.
einfaches Beispiel
Ein Beispiel für eine solche Schaltung ist in Abbildung ## gegeben. Hier ist $I_0$ gesucht. Dieser Strom kann über die (gegebene) Spannung $U_0$ und den Gesamtwiderstand zwischen den Klemmen $a$ und $b$ ermittelt werden. Gesucht ist also $R_{ab}$.
Wie bereits in den vorherigen Unterkapitel beschrieben, können hier auch Teilschaltung schrittweise in Ersatzwiderstände umgewandelt werden. Wichtig dabei ist, dass diese Teilschaltungen zur Umwandlung in Ersatzwiderstände immer nur zwei Anschlüsse (= zwei Knoten zur „Außenwelt“) haben dürfen.
Abbildung ## zeigt die schrittweise Umwandlung der Ersatzwiderstände an diesem Beispiel.
Als Ergebnis des Ersatzwiderstands erhält man:
\begin{align*} R_g = R_{12345} &= R_{12}||R_{345} = R_{12}||(R_3+R_{45}) = (R_1||R_2)||(R_3+R_4||R_5) \\ &= {{ {{R_1 \cdot R_2}\over{R_1 + R_2}} \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) }\over{ {{R_1 \cdot R_2}\over{R_1 + R_2}} +R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}} }} \quad \quad \quad \quad \quad \quad \bigg\rvert \cdot{{(R_1 + R_2) \cdot (R_4 + R_5)}\over{(R_1 + R_2) \cdot (R_4 + R_5)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 + {{R_4 \cdot R_5}\over{R_4 + R_5}}) \cdot (R_4 + R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ &= {{ R_1 \cdot R_2 \cdot (R_3 \cdot (R_4 + R_5) + R_4 \cdot R_5) } \over { R_1 \cdot R_2\cdot(R_4 + R_5) +R_3 + R_4 \cdot R_5 \cdot (R_1 + R_2)}} \\ \end{align*}
Beispiel mit Dreieck-Stern-Transformation
Mit der Dreieck-Stern-Transformation lässt sich nun auch das anfängliche Beispiel umwandeln. Bei komplizierteren Schaltungen ist die wiederholte Dreieck-Stern-Transformation mit anschließendem Zusammenfassen der Widerstände sinnvoll, solange bis die entstandene Schaltung leicht mit Knoten- und Maschensatz berechenbar wird (Abbildung ##). Hier wird auf eine Rechnung verzichtet - es empfiehlt sich hier mit Zwischenergebnissen für die transformierten Widerständen zu rechnen.
Beispiel mit Symmetrien in der Schaltung
Ein gewisser Sonderfall betrifft mögliche Symmetrien in Schaltungen. Falls dies3 vorhanden sind, kann eine weitere Vereinfachung vorgenommen werden.
Abbildung ## zeigt links ein symmetrischen Aufbau eines Netzwerks aus jeweils gleichen Widerständen $R$. Zum Verständnisgewinn ist in der Mitte in der gleichen Schaltung zusätzlich Schalter und Testpunkte (TP) verbaut, welche die Spannung gegen Masse anzeigen.
Über die Schalter kann nachgeprüft werden, ob ein Strom fließt, falls die jeweiligen Knoten verbunden werden. In der Simulation ist zu sehen, dass dies nicht der Fall ist. Im symmetrischen Aufbau sind diese Knoten jeweils auf dem gleichen Potential.
Damit lässt sich die Schaltung auch in die Form bringen, wie sie in Abbildung ## rechts zu sehen ist. Diese Schaltung ist wiederum leicht berechenbar:
\begin{align*} R_g = R || R + R || R || R || R + R || R || R || R + R || R = {{1}\over{2}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{4}}\cdot R + {{1}\over{2}}\cdot R = 1,5\cdot R \end{align*}
Exercise 2.7.1 Aufgabe zur Schaltungsvereinfachung I
Exercise 2.7.2 Aufgabe zur Schaltungsvereinfachung II + III
Exercise 2.7.3 Aufgabe zur Schaltungsvereinfachung IV
Exercise 2.7.4 Aufgabe zur Schaltungsvereinfachung IV
Exercise 2.7.5 Aufgabe zur Schaltungsvereinfachung V
Exercise 2.7.6 Aufgabe zur Schaltungsvereinfachung VI
Exercise 2.7.7 Simplifying Circuits (exam task, about 8% of a 60-minute exam, WS2020)
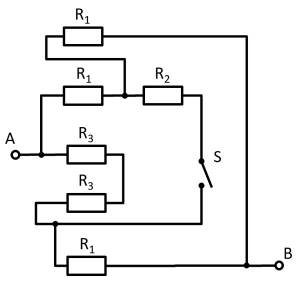
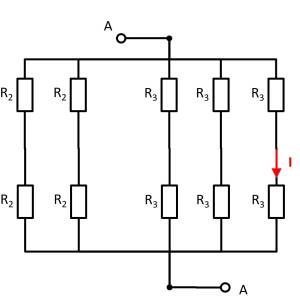
Given is the adjoining circuit with
$R_1=10 ~\Omega$
$R_2=20 ~\Omega$
$R_3=5 ~\Omega$
and the switch $S$.
1. Determine the total resistance $R_{\rm eq}$ between A and B by summing the resistances with the switch $S$ open.
- How can the circuit be better represented or pulled apart?
- The switch should be replaced by an open wire in this case.
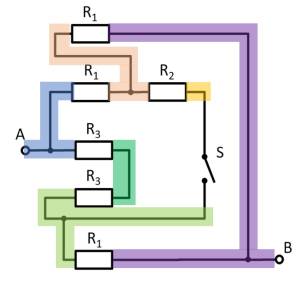
For this purpose, the individual branches can be highlighted in color and interpreted as a „conductive rubber band“.
This results in:
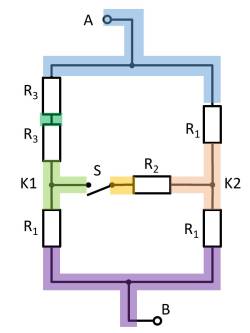
Thus $R_3$ and $R_3$ can be combined to $R_{33} = 2 \cdot R_3 = R_1$, yielding a left and a right voltage divider.
Now it is visible that in the left and right voltage divider, the same potential is at the respective branch, or at the node K1 (green) and K2 (pink).
Thus, the total resistance can be calculated as $R_{\rm eq} = (2 \cdot R_1)||(2 \cdot R_1)$.
However, by symmetry, nodes K1 and K2 can also be short-circuited. Thus, $R_{\rm eq} = 2 \cdot \left( R_1||R_1 \right)$ also holds.
2. What is the total resistance when switch $S$ is closed?
So the resistance remains the same.
Exercise 2.7.8: Simplifying Circuits II (written exam task, approx 8% of a 60-minute written exam, WS2020)
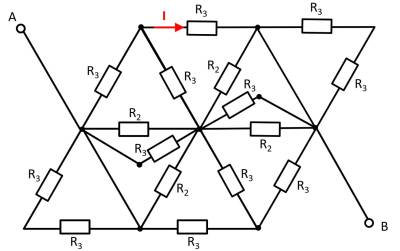
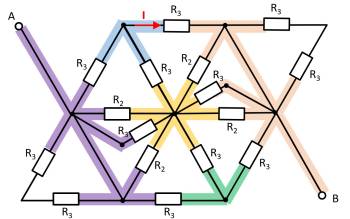
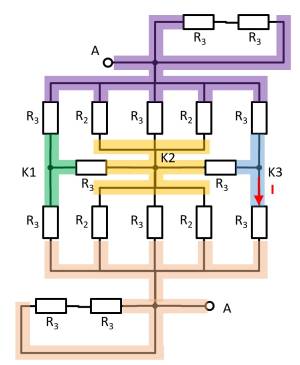
Given is the adjoining circuit with
$R_1=5 ~\Omega$
$R_2=10 ~\Omega$
$R_3=20 ~\Omega$
1. Determine the equivalent resistance $R_{\rm eq}$ between A and B by summing the resistances.
- How can the circuit be better represented or pulled apart?
- Switches (when used) should be replaced by an open or closed circuit.
- Does this result in equal potentials at different nodes that can be cleverly used?
For this purpose, the individual branches can be highlighted in color and interpreted as a „conductive rubber band“.
It can be seen that the two resistors $R_3$ at the top left and bottom right are each shorted. The result is thus:
Here it helps to consider the potential of the nodes K1, K2, and K3. For K2, the resistances $R_2 || R_3 || R_2$ must be combined at the top and bottom. Thus, the same resistance values at the top and bottom result. Also at the nodes K1 and K2 the same resistance values at the top and at the bottom result. With the same ratios of the resistances at K1, K2, and K3 respectively, it can be concluded that no current flows across the resistors $R_3$ between K1 and K2 or K2 and K3. Thus, these do not contribute to the total resistance. In such a case, a short circuit or an open line can be freely chosen between the relevant nodes for the calculation. In the following, an open line is chosen. Additionally, the parallel strings can be reordered.
This results in:
\begin{align*} R_{\rm eq} &= \left( \left( 2 \cdot R_2 \right) || \left( 2 \cdot R_2 \right) \right) && || \; \left( \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\left( R_3 || \left( 2 \cdot R_3 \right) \right) \\ R_{\rm eq} &= R_2 && || \;\frac{R_3 \cdot 2 R_3}{R_3 + 2 R_3} \\ R_{\rm eq} &= R_2 && || \;\frac{2}{3}\cdot R_3 \\ R_{\rm eq} &= \frac{R_2 \cdot \frac{2}{3}\cdot R_3}{R_2 + \frac{2}{3}\cdot R_3} \\ R_{\rm eq} &= \frac{R_2 \cdot R_3}{\frac{3}{2}\cdot R_2 + R_3} \\ \\ \end{align*}
2. Now let the voltage from A to B be: $U_{AB}=U_0= 20 ~\rm V$. What is the current $I$?
Exercise 2.7.9 - Variation: Simplifying Circuits II (written exam task, approx 8% of a 60-minute written exam, WS2020)
Given is the adjoining circuit with
$R_1=10 ~\Omega$
$R_2=20 ~\Omega$
$R_3=5 ~\Omega$
1. Determine the equivalent resistance $R_{\rm eq}$ between A and B by summing the resistances.
2. Now let the voltage from A to B be: $U_{\rm AB}=U_0= 10 ~\rm V$. What is the current $I$?
Exercise 2.7.10 - Variation: Simplifying Circuits III (written exam task, approx 8% of a 60-minute written exam, WS2020)
weitere Exercises
Weitere Anfgaben sind Online auf den Seiten von HErTZ zu finden (Auswahl links im Menu).